Luận án Các thuật toán gần đúng giải bài toán cây khung với chi phí định tuyến nhỏ nhất

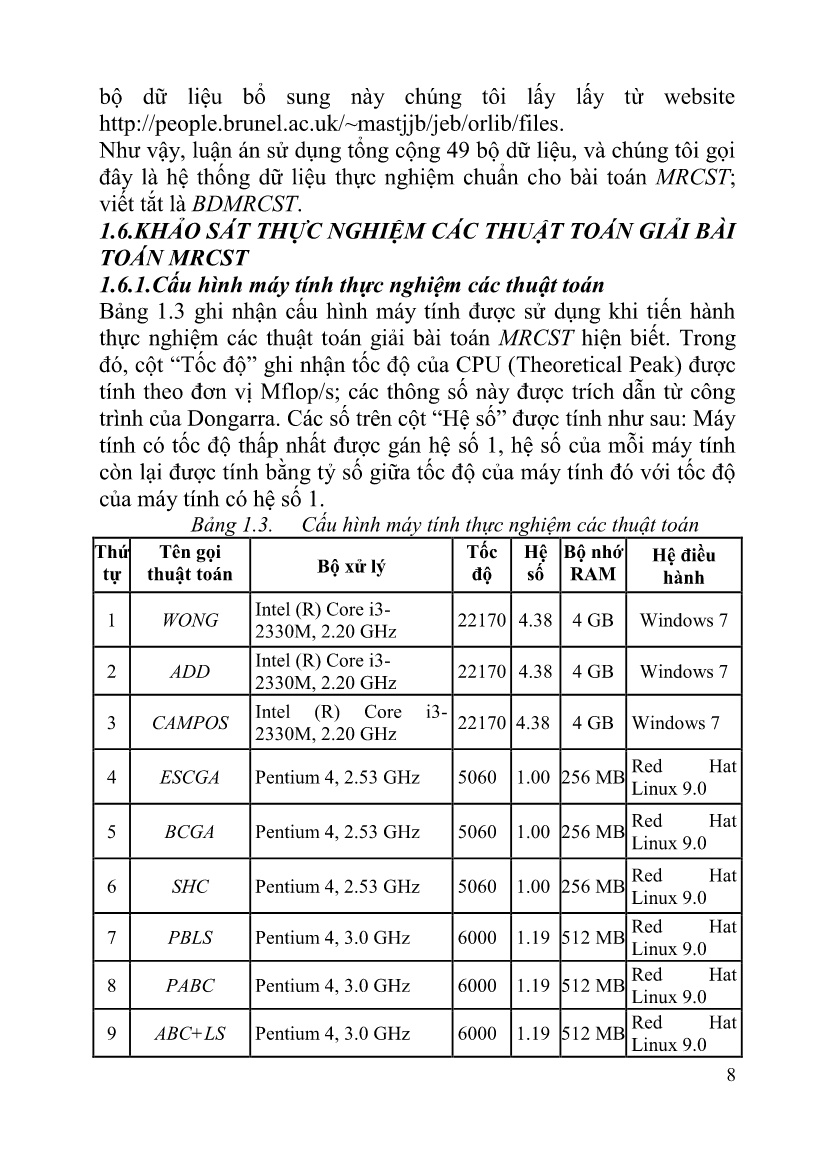
SCGA Pentium 4, 2.53 GHz 5060 1.00 256 MB 
 Linux 9.0 
 Red Hat 
 5 BCGA Pentium 4, 2.53 GHz 5060 1.00 256 MB 
 Linux 9.0 
 Red Hat 
 6 SHC Pentium 4, 2.53 GHz 5060 1.00 256 MB 
 Linux 9.0 
 Red Hat 
 7 PBLS Pentium 4, 3.0 GHz 6000 1.19 512 MB 
 Linux 9.0 
 Red Hat 
 8 PABC Pentium 4, 3.0 GHz 6000 1.19 512 MB 
 Linux 9.0 
 Red Hat 
 9 ABC+LS Pentium 4, 3.0 GHz 6000 1.19 512 MB 
 Linux 9.0 
 8 
1.6.2.Chất lượng lời giải 
Kết quả thực nghiệm từ các thuật toán đã công bố của các tác giả 
khác như ESCGA, BCGA, SHC, PBLS, PABC, ABC+LS trên các đồ 
thị đầy đủ Euclid và đồ thị đầy đủ ngẫu nhiên được trích nguyên 
gốc từ các công trình tương ứng. Với 14 bộ dữ liệu là các đồ thị 
thưa; do chưa có một công trình nào công bố chất lượng lời giải, 
nên chúng tôi đã cài đặt lại các thuật toán SHC, PBLS, ABC+LS 
trên cùng môi trường triển khai các thuật toán đề xuất trong luận 
án. Để kiểm tra chất lượng các chương trình do chúng tôi cài đặt, 
chúng tôi đã đối sánh output từ các chương trình do chúng tôi cài 
đặt với output mà các tác giả đã công bố (trên các bộ dữ liệu đã có 
kết quả công bố). 
Chi phí định tuyến trong các bảng thực nghiệm được ghi nhận bằng 
½ giá trị tính theo công thức (1-2). 
Đánh giá chung trên 49 bộ dữ liệu thì các thuật toán được xếp hạng 
theo chất lượng lời giải như sau: ABC+LS, PABC, PBLS, SHC, 
ESCGA, BCGA, CAMPOS, WONG, ADD. 
Từ chất lượng lời giải thu được trên, luận án rút ra một số nhận xét 
sau: Đối với đồ thị đầy đủ Euclid, trong các thuật toán nhanh 
WONG, CAMPOS, ADD thì thuật toán CAMPOS cho chất lượng lời 
giải tốt nhất; thuật toán ABC+LS cho chất lượng lời giải tốt nhất 
trong số tất cả các thuật toán đã khảo sát. Đối với đồ thị đầy đủ 
ngẫu nhiên, trong các thuật toán nhanh thì thuật toán WONG cho 
chất lượng lời giải tốt nhất; các thuật toán SHC, PBLS, PABC, 
ABC+LS cho chất lượng lời giải tương đương và chúng cho chất 
lượng lời giải tốt hơn các thuật toán di truyền ESCGA, BCGA. 
1.6.3.Thời gian tính 
Thời gian thực nghiệm trong luận án được tính theo đơn vị giây. 
Thời gian tính của các thuật toán metaheuristic ESCGA, BCGA, 
SHC, PBLS, PABC, ABC+LS đã được công bố trong các công trình 
tương ứng. 
Thời gian tính các thuật toán trên các máy tính khác nhau đã được 
quy đổi về một mức theo trên cơ sở của công trình Dongarra. 
1.7.KẾT LUẬN CHƯƠNG 1 
Chương này đã trình bày một số nội dung chính sau: Thứ nhất, giới 
thiệu bài toán MRCST; MRCST là bài toán thuộc lớp bài toán NP-
 9 
khó. Thứ hai, trình bày về ứng dụng của bài toán MRCST trong lĩnh 
vực mạng truyền thông và trong tin sinh học. Thứ ba, giới thiệu một 
số thuật toán gần đúng điển hình giải bài toán MRCST như WONG, 
GENERAL STAR, PTAS, ADD, CAMPOS, ESCGA, BCGA, SHC, 
PBLS, PABC, ABC+LS; cũng trong phần này, luận án đã giới thiệu 
một số công việc liên quan như mã hóa cây khung, tính chi phí định 
tuyến của cây khung và một số cách thức tạo lời giải ban đầu được 
áp dụng trong các thuật toán metaheuristic giải bài toán MRCST. 
Thứ tư, trình bày tiêu chí đánh giá chất lượng thuật toán giải gần 
đúng. Thứ năm, giới thiệu chi tiết về hệ thống dữ liệu thực nghiệm 
chuẩn cho bài toán MRCST và ghi nhận kết quả thực nghiệm của các 
thuật toán trên đối với hệ thống dữ liệu thực nghiệm chuẩn này. Từ 
khảo sát thực nghiệm khẳng định tiếp cận giải bài toán MRCST theo 
hướng metaheuristic là có tiềm năng nhất. Trong đó, thuật toán 
ABC+LS cho chất lượng lời giải tốt hơn các thuật toán gần đúng 
hiện biết trên đồ thị đầy đủ Euclid. 
Chương này có một số đóng góp cụ thể sau: Về mặt lý thuyết, luận 
án đã đề xuất định lý đánh giá cận trên và cận dưới của tải định 
tuyến một cạnh thuộc cây khung (Định lý 1.2), từ đó đưa ra hệ quả 
1.1 và hệ quả 1.2 về cận trên và cận dưới của chi phí định tuyến 
một cây khung. Về mặt thực nghiệm, luận án đã đề xuất bổ sung 14 
bộ dữ liệu thực nghiệm là các đồ thị thưa có kích thước lớn. Để 
đánh giá các thuật toán hiện có trên các bộ dữ liệu bổ sung, chúng 
tôi đã cài đặt lại các thuật toán WONG, SHC, PBLS, ABC+LS trên 
cùng môi trường mà luận án đã triển khai. 
Kết quả chính của chương này đã được nghiên cứu sinh công bố tại 
hội nghị SocPar 2013. 
 Chương 2. THUẬT TOÁN TÌM KIẾM LEO ĐỒI 
Hầu hết các đồ thị gặp trong thực tế ứng dụng là đồ thị thưa. Các 
thuật toán metaheuristic gần đây giải bài toán MRCST như SHC, 
PBLS, PABC, ABC+LS được thực nghiệm trên các đồ thị đầy đủ 
Euclid và đồ thị đầy đủ ngẫu nhiên. Khi thực nghiệm các thuật toán 
này trên các đồ thị thưa thì chất lượng lời giải không có sự vượt trội 
nào trong khi thời gian thực hiện lại chậm đáng kể. 
Chương này đề xuất hai thuật toán HCSRI và HCSIR giải bài toán 
MRCST – trong đó có đề xuất cách thức tìm kiếm lân cận mới. Các 
 10 
thuật toán HCSRI và HCSIR được phát triển dựa trên sơ đồ của thuật 
toán tìm kiếm leo đồi. Qua thực nghiệm cho thấy các đề xuất này 
cho lời giải với chất lượng cạnh tranh được với các thuật toán cùng 
lớp là SHC, PBLS và các thuật toán PABC, ABC+LS trên các loại đồ 
thị thưa và đồ thị đầy đủ ngẫu nhiên nhưng với thời gian tính nhanh 
hơn. Các thuật toán HCSRI, HCSIR cũng đã cho chất lượng lời giải 
tốt hơn hẳn các thuật toán heuristic và các thuật toán di truyền đã 
được công bố trước đó như WONG, ADD, CAMPOS, ESCGA, 
BCGA trên hệ thống dữ liệu thực nghiệm chuẩn. 
2.1.CÂY KHUNG LÂN CẬN 
Cho đồ thị vô hướng liên thông có trọng số G. Để ngắn gọn, trong 
các phần tiếp theo ta sẽ sử dụng ký hiệu T–{e} (hoặc T {e}) là đồ 
thị thu được từ T bởi việc loại cạnh e (hoặc chèn thêm vào cạnh e). 
Mục này đưa ra một số định nghĩa về cây khung lân cận. 
Định nghĩa 2.1. (1-lân cận của cây khung T) Cho đồ thị G và T là 
một cây khung của nó. Ta gọi 1-lân cận của cây khung T là tập tất 
cả các cây khung của đồ thị G sai khác với T không quá một cạnh. 
Nếu T’ là một cây khung thuộc 1-lân cận của T thì ta nói T và T’ là 
1-lân cận với nhau. 
Như vậy, nếu T’ là cây khung thuộc 1-lân cận của cây khung T (T’ 
T), thì tìm được cạnh e E(T) và cạnh e’ E(T’) sao cho E(T’)= 
E(T) –{e}  {e’}, nghĩa là cây T’ thu được từ cây T bằng cách loại 
cạnh e và sau đó thêm vào cạnh e’. 
Trong một số trường hợp chúng ta còn sử dụng những lân cận rộng 
hơn so với 1-lân cận. Khái niệm k-lân cận dưới đây là mở rộng trực 
tiếp của khái niệm 1-lân cận. 
Định nghĩa 2.2. (k-lân cận của cây khung T) Cho đồ thị G và T là 
một cây khung của nó. Ta gọi k-lân cận của cây khung T là tập tất 
cả các cây khung của đồ thị G sai khác với T không quá k cạnh. Nếu 
T’ là một cây khung thuộc k-lân cận của T thì ta nói T và T’ là k-lân 
cận với nhau. 
Như vậy, nếu T’ là cây khung thuộc k-lân cận của cây khung T (T’ 
T), thì tìm được tập cạnh X  E(T) và tập cạnh X’  E(T’) sao cho 
|X| = |X’| ≤ k và E(T’)= E(T) – X  X’, nghĩa là cây T’ thu được từ 
cây T bằng cách loại tập cạnh X và sau đó thêm vào tập cạnh X’. 
Định nghĩa 2.3. (Lân cận tất định và lân cận ngẫu nhiên) Nếu các 
 11 
cây khung trong lân cận được xác định không phụ thuộc vào yếu tố 
ngẫu nhiên thì ta nói về lân cận tất định, còn nếu ngược lại, ta nói về 
lân cận ngẫu nhiên. 
Thuật toán tìm kiếm leo đồi ngẫu nhiên (Stochastic Hill Climber- 
SHC) là thuật toán dạng 1-lân cận ngẫu nhiên. Các thuật toán tìm 
kiếm leo đồi HCSRI, HCSIR là sử dụng 1-lân cận tất định. 
2.2.THUẬT TOÁN HCSRI 
2.2.1.Ý tưởng thuật toán HCSRI 
Bắt đầu từ cây khung T của G được khởi tạo ngẫu nhiên bằng thuật 
toán LikePrim (tìm cây khung ngẫu nhiên theo ý tưởng của thuật 
toán Prim nhưng không quan tâm đến trọng số cạnh), loại lần lượt 
từng cạnh e E(T), với mỗi cạnh e như vậy, tìm một cạnh e’ 
E(G) – E(T) sao cho cây khung T' = (T –{e}) {e’} có chi phí định 
tuyến nhỏ nhất. Nếu C(T’) < C(T) thì thay T bằng T’ (thay cạnh e 
trong T bằng cạnh e’ trong E(G) – E(T)). Thuật toán dừng nếu trong 
một lần duyệt qua tất cả các cạnh e E(T) mà không tìm được cạnh 
e’ để cải thiện chi phí định tuyến của cây khung T. 
Thao tác quan trọng của thuật toán HCSRI là việc kiểm tra xem với 
mỗi cạnh e’ E – E(T), đồ thị T –{e}  {e’} có là một cây khung 
hay không? Thao tác này được giải quyết như sau: Ghi nhận hai tập 
V(T1) và V(T2) tương ứng là các tập đỉnh của hai cây con T1, T2 
được tạo thành từ cây khung T khi loại cạnh e khỏi cây khung T. 
Cạnh e’=(u,v) E – E(T) có thể chèn được vào T – {e} khi u và v 
không thuộc cùng một trong hai tập V(T1) và V(T2). 
Độ phức tạp một lần lặp của thuật toán HSCRI là O(kn2m). 
2.3.THUẬT TOÁN HCSIR 
Cho đồ thị vô hướng liên thông có trọng số G. Bắt đầu từ cây khung 
T của G được khởi tạo ngẫu nhiên bằng thuật toán LikePrim, chèn 
lần lượt từng cạnh e E(G)–E(T) vào cây khung T, khi đó E(T)  
{e} sẽ chứa một chu trình, tìm một cạnh e’ trên chu trình này sao 
cho việc loại nó dẫn đến cây khung T’ có chi phí định tuyến là nhỏ 
nhất. Nếu C(T') < C(T) thì thay T bằng T' (hoán đổi cạnh e trong 
E(G) – E(T) với cạnh e’ trong T). Thuật toán dừng nếu trong một 
lần duyệt qua tất cả các cạnh e E(G) – E(T) mà không cải thiện 
được chi phí định tuyến của cây khung T. 
Thao tác quan trọng của thuật toán HCSIR là việc tìm chu trình 
 12 
trong T sau khi chèn thêm cạnh. Khi chèn cạnh e =(u,v) vào T, 
duyệt cây khung T theo chiều sâu bắt đầu từ u, lưu vết trên đường 
đi bằng mảng p (đỉnh trước của một đỉnh trong phép duyệt). Tiếp 
theo, bắt đầu từ đỉnh v, truy vết theo mảng p đến khi gặp u thì kết 
thúc, các cạnh trên đường truy vết chính là các cạnh trong chu trình 
cần tìm. 
Ta nhận thấy tập các lân cận của một cây khung T theo kết quả tìm 
kiếm của hai thuật toán này là tương đương, tuy nhiên do thứ tự các 
cạnh được chọn tại một thời điểm ảnh hướng đến kết quả của mọi 
thời điểm sau đó; vì vậy chúng tôi xem đây là hai chiến lược tìm 
kiếm khác nhau. 
Độ phức tạp một lần lặp của thuật toán HSCIR là O(kn2m). 
Các thuật toán HCSRI và HCSIR ngoài việc lời giải ban đầu được 
khởi tạo ngẫu nhiên thì các cây khung lân cận tìm được trong quá 
trình tìm kiếm là kiểu 1-lân cận tất định. Hiệu quả của các thuật 
toán HCSRI, HCSIR có thể được cải thiện khi ta thay đổi thứ tự các 
cạnh được duyệt trong tập E(G) – E(T); nghĩa là ta sẽ duyệt tập 
cạnh này theo một hoán vị được sinh ngẫu nhiên chứ không theo 
một thứ tự cố định ở tất cả các lần duyệt. 
Các thuật toán HCSRI, HCSIR; chủ yếu sử dụng tính tăng cường; 
thể hiện qua các chiến lược tìm kiếm cây khung lân cận; tính đa 
dạng được sử dụng vào hai thời điểm sau: thứ nhất là khi khởi tạo 
lời giải ban đầu; thứ hai là thay đổi thứ tự duyệt của các cạnh trong 
tập cạnh ứng viên (như đã đề cập ở đoạn trên). Hai chiến lược tăng 
cường hóa và đa dạng hóa được sử dụng trong các thuật toán 
HCSRI, HCSIR là khác so với chiến lược tăng cường hóa và đa 
dạng hóa được sử dụng trong các thuật toán cùng nhóm được công 
bố trước đó như SHC, PBLS. 
Các thuật toán HCSRI, HCSIR có độ phức tạp thời gian tính cho một 
lần lặp là O(kn2m). Trong khi các thuật toán SHC, PBLS đưa ra số 
lần lặp khá lớn để đạt được kết quả như công bố; thì các thuật toán 
HCSRI, HCSIR với cách thức tìm lân cận đã nêu có giá trị k khá 
nhỏ. Thời gian tính của các thuật toán HCSRI, HCSIR nhanh hơn so 
với nhiều thuật toán metaheuristic khác, đặc biệt là khi làm việc với 
các đồ thị thưa. 
2.4.THỰC NGHIỆM VÀ ĐÁNH GIÁ 
 13 
Chúng tôi tiến hành thực nghiệm các thuật toán HCSRI, HCSIR trên 
BDMRCST. Với mỗi loại đồ thị, chúng tôi so sánh chất lượng lời 
giải và thời gian tính của các thuật toán HCSRI, HCSIR với các 
thuật toán của các tác giả khác đã khảo sát như WONG, ADD, 
CAMPOS, ESCGA, BCGA, SHC, PBLS. 
2.4.1.Môi trường thực nghiệm 
Các thuật toán HCSRI, HCSIR được cài đặt trên ngôn ngữ C++ sử 
dụng môi trường DEV C 5.0, CPU INTEL i3-2330M, 2.20 GHz, bộ 
nhớ 4GB RAM, hệ điều hành Windows 7. 
2.4.2.Tham số thực nghiệm 
Các thuật toán HCSRI, HCSIR đều cho thực hiện 60 lần trên mỗi bộ 
dữ liệu đồ thị đầy đủ Euclid và 30 lần trên mỗi bộ dữ liệu là các đồ 
thị đầy đủ ngẫu nhiên và đồ thị thưa. Lời giải ban đầu của mỗi lần 
chạy được cho khởi tạo bằng thuật toán LikePrim. Mỗi lời giải hiện 
tại đều cho tìm 1-lân cận tất định tốt nhất trong số tất cả các 1-lân 
cận có thể có theo ý tưởng của thuật toán HCSRI, HCSIR tương 
ứng. 
2.4.3.Chất lượng lời giải 
Đánh giá chung, với 49 bộ dữ liệu trên, thuật toán HCSRI cho chất 
lượng lời giải tốt hơn (tồi hơn) các thuật toán WONG (100.0%, 
0.0%), ADD (100.0%, 0.0%), CAMPOS (100.0%, 0.0%), ESCGA 
(88.6%, 0.0%), BCGA (100.0%, 0.0%), SHC (36.7%, 2.0%), PBLS 
(8.2%, 18.4%). 
Đánh giá chung, với 49 bộ dữ liệu trên, thuật toán HCSIR cho chất 
lượng lời giải tốt hơn (tồi hơn) các thuật toán WONG (100.0%, 
0.0%), ADD (100.0%, 0.0%), CAMPOS (100.0%, 0.0%), ESCGA 
(88.6%,0.0%), BCGA (100.0%, 0.0%), SHC (36.7%, 6.1%), PBLS 
(6.1%, 22.4%). 
2.4.4.Thời gian tính 
Thời gian tính được ghi nhận ở đây là thời gian trung bình của các 
lần chạy. 
Thuật toán HCSRI có thời gian tính nhanh hơn các thuật toán 
metaheuristic ESCGA, BCGA, SHC, PBLS. Cụ thể, với tất cả 35 bộ 
dữ liệu đồ thị đầy đủ của Julstrom; thuật toán HCSRI có thời gian 
tính chỉ bằng không quá 7.22% thời gian tính của thuật toán 
ESCGA, không quá 18.60% thời gian tính của thuật toán BCGA, 
không quá 17.31% thời gian tính của thuật toán SHC, không quá 
 14 
8.04% thời gian tính của thuật toán PBLS. Với tất cả các bộ dữ liệu 
là đồ thị thưa, thuật toán HCSRI có thời gian tính chỉ bằng không 
quá 1.29% thời gian tính của thuật toán SHC và không quá 13.13% 
thời gian tính của thuật toán PBLS. 
Thuật toán HCSIR có thời gian tính nhanh hơn các thuật toán 
metaheuristic ESCGA, BCGA, SHC, PBLS. 
Thời gian tính của các thuật toán HCSRI, HCSIR chậm hơn rất 
nhiều so với thời gian tính của các thuật toán WONG, ADD, 
CAMPOS. 
2.5.KẾT LUẬN CHƯƠNG 2 
Chương này đề xuất hai thuật toán HCSRI, HCSIR giải bài toán 
MRCST; đây là các thuật toán dạng tìm kiếm leo đồi. Cây khung lân 
cận trong quá trình tìm kiếm của hai thuật toán HCSRI, HCSIR là 
dạng 1-lân cận tất định. Các đề xuất này luôn cho chất lượng lời 
giải tốt hơn các thuật toán WONG, ADD, CAMPOS, ESCGA, 
BCGA trên hệ thống dữ liệu thực nghiệm chuẩn. Thuật toán HCSRI, 
HCSIR luôn cho chất lượng lời giải tốt hơn hoặc bằng các thuật 
toán metaheuristic SHC, PBLS trên các đồ thị đầy đủ ngẫu nhiên và 
đồ thị thưa. Đối với các đồ thị đầy đủ Euclid thì các thuật toán 
HCSRI, HCSIR cho chất lượng lời giải tồi hơn thuật toán PBLS ở 
một số bộ dữ liệu. Trong mọi bộ dữ liệu, các thuật toán HCSRI, 
HCSIR luôn cho thời gian tính nhanh hơn so với các thuật toán 
metaheuristic SHC, PBLS, ESCGA, BCGA. Đề xuất này có ý nghĩa 
quan trọng đối với các đồ thị thưa có nhiều đỉnh. 
Các kết quả chính của chương này là một bài báo đã được báo cáo 
tại hội nghị IMLC vào tháng 2 năm 2011, sau đó bài báo được 
chỉnh sửa và công bố ở tạp chí IJMLC [1] tháng 8/2012. 
 Chương 3. THUẬT TOÁN DI TRUYỀN 
Các thuật toán di truyền ESCGA, BCGA của Bryant A. Julstrom 
mặc dù đã cho lời giải chất lượng tốt hơn các thuật toán đề xuất 
trước đó như WONG, ADD; tuy nhiên hai phép toán di truyền cơ 
bản nhất của ESCGA, BCGA được thiết kế không có tính định 
hướng về chi phí định tuyến; mà chúng được thực hiện hoàn toàn 
ngẫu nhiên; chính điều này đã làm cho ESCGA, BCGA thiếu đi các 
tính đa dạng và tăng cường; đây là yếu tố chính làm cho chất lượng 
lời giải của các thuật toán ESCGA, BCGA không như mong muốn. 
 15 
Chương này đề xuất thuật toán có tên gọi là GST để giải bài toán 
MRCST, thuật toán GST thuộc dạng thuật toán di truyền. Thuật toán 
GST đề xuất phép lai và đột biến mới có tính định hướng đến chi 
phí định tuyến; các phép lai và đột biến này có tính đa dạng và tính 
tăng cường cao hơn. Qua thực nghiệm cho thấy, thuật toán GST cho 
lời giải với chất lượng tốt hơn và thời gian tính nhanh hơn so với các 
thuật toán ESCGA, BCGA; thuật toán GST cũng cho lời giải với chất 
lượng tốt hơn các thuật toán WONG, ADD, CAMPOS, SHC. 
3.1.THUẬT TOÁN GST 
Mục này luận án trình bày thuật toán các thủ tục giải quyết bài toán 
MRCST dựa trên sơ đồ của thuật toán di truyền cơ bản. 
Thuật toán GST sử dụng thuật toán LikePrim đã trình bày trong 
chương 1 để tạo quần thể ban đầu P. 
Phép lai của thuật toán GST mà chúng tôi đề xuất là phép lai mới; 
có định hướng đến chi phí định tuyến; có tính tăng cường cao hơn 
so với các phép lai đã được sử dụng trong các thuật toán di truyền 
ESCGA, BCGA. 
Phép đột biến mà chúng tôi đề xuất trong thuật toán GST là phép 
đột biến mới; có tính tăng cường và tính đa dạng cao hơn so với các 
thuật toán di truyền ESCGA, BCGA. 
Thuật toán GST sử dụng phép chọn lọc các cá thể dựa trên độ thích 
nghi xếp hạng. 
Để không làm mất đi cá thể tốt nhất đã được khai phá trong quá 
trình tiến hóa, Thuật toán GST luôn cập nhật cá thể tốt nhất cho đến 
thời điểm hiện tại. 
Sơ đồ thuật toán GST 
Quần thể cây khung ban đầu được khởi tạo ngẫu nhiên, tiến hành 
đánh giá độ thích nghi cho mỗi cá thể. Thuật toán GST lặp lại các 
công việc sau cho đến khi điều kiện dừng được thỏa: Thực hiện 
phép lai các cá thể cây khung để hình thành thêm các cá thể cây 
khung mới; trên quần thể mới sau khi lai, thực hiện phép đột biến; 
tiếp theo thực hiện phép đa dạng hóa quần thể, phép chọn các cá thể 
cây khung dựa trên độ thích nghi xếp hạng và cuối cùng là cập nhật 
cá thể có độ thích nghi tốt nhất cho đến thệ hệ tiến hóa hiện tại. 
So với các thuật toán di truyền đã công bố trước đó như ESCGA, 
BCGA; phép lai và đột biến của thuật toán GST được chúng tôi thiết 
 16 
kế có tính định hướng về chi phí định tuyến; do đó làm cho thuật 
toán GST có tính đa dạng cao hơn và tăng cường mạnh mẻ hơn. 
Độ phức tạp một lần lặp của thuật toán GST là O(N2n2). 
3.2.THỰC NGHIỆM VÀ ĐÁNH GIÁ 
Chúng tôi tiến hành thực nghiệm thuật toán GST trên BDMRCST. 
Với mỗi loại đồ thị, chúng tôi so sánh chi phí định tuyến và thời 
gian tính thuật toán GST với các thuật toán của các tác giả khác là 
WONG, CAMPOS, ESCGA, BCGA, SHC, PBLS. 
Chất lượng lời giải 
Đánh giá chung, với 49 bộ dữ liệu trên, thuật toán GST cho chất 
lượng lời giải tốt hơn (tồi hơn) các thuật toán WONG (100.0%, 
0.0%), CAMPOS (100.0%, 0.0%), ESCGA (88.6%, 0.0%), BCGA 
(100.0%, 0.0%), SHC (38.8%, 2.0%), PBLS (10.2%, 14.3%). 
Thời gian tính 
Thuật toán GST có thời gian tính nhanh hơn các thuật toán ESCGA, 
BCGA, SHC, PBLS trên mọi bộ dữ liệu đồ thị đầy đủ của Julstrom; 
nhưng chậm hơn các thuật toán SHC, PBLS trên các đồ thị thưa. Cụ 
thể, với tất cả 35 bộ dữ liệu đồ thị đầy đủ của Julstrom; thuật toán 
GST có thời gian tính chỉ bằng không quá 18.22% thời gian tính của 
thuật toán ESCGA, không quá 18.22% thời gian tính của thuật toán 
ESCGA, không quá 45.10% thời gian tính của thuật toán BCGA, 
không quá 42.07% thời gian tính của thuật toán SHC, không quá 
38.62% thời gian tính của thuật toán PBLS. Với các đồ thị thưa, 
thuật toán GST có thời gian tính chậm hơn thời gian tính của các 
thuật toán SHC, PBLS không dưới 234.05%. 
Thuật toán GST có thời gian tính chậm hơn rất nhiều so với các 
thuật toán WONG, CAMPOS. 
3.3.KẾT LUẬN CHƯƠNG 3 
Chương này đề xuất thuật toán GST giải bài toán MRCST. Cụ thể 
trong thuật toán này chúng tôi đã đề xuất phép lai và phép đột biến 
mới so với phép lai và đột biến trong các thuật toán di truyền đã 
công bố trước đó là ESCGA, BCGA. Thuật toán GST cho chất 
lượng lời giải tốt hơn các thuật toán ESCGA, BCGA, WONG, 
CAMPOS, SHC trên phần lớn các bộ dữ liệu thuộc hệ thống dữ liệu 
thực nghiệm chuẩn. Thuật toán GST cho thời gian tính nhanh hơn 
các thuật toán ESCGA, BCGA, SHC, PBLS trên tất cả các đồ thị đầy 
đủ Euclid và đồ thị đầy đủ ngẫu nhiên. 
 17 
Các kết quả chính của chương này đầu tiên được nghiên cứu sinh 
báo cáo tại hội nghị IMLC vào tháng 2 năm 2011 và sau khi chỉnh 
sửa đã công bố trong tạp chí IJMLC [2] tháng 8/2012. 
 Chương 4. THUẬT TOÁN TÌM KIẾM TABU 
Các thuật toán HCSRI, HCSIR có ưu điểm nổi bật khi giải quyết các 
bài toá