Luận án Giảm can nhiễu trong hệ thống MIMO - OFDM

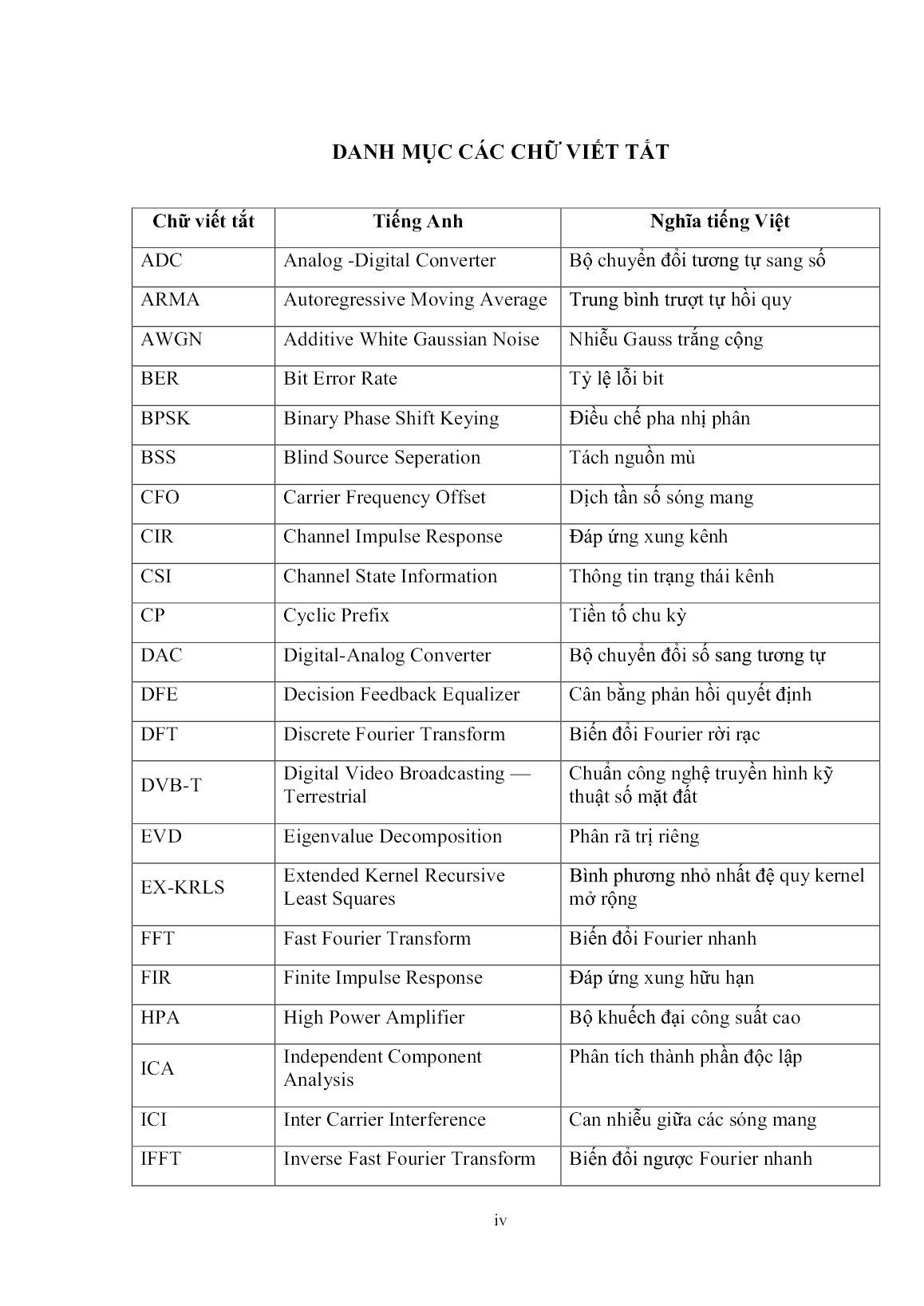
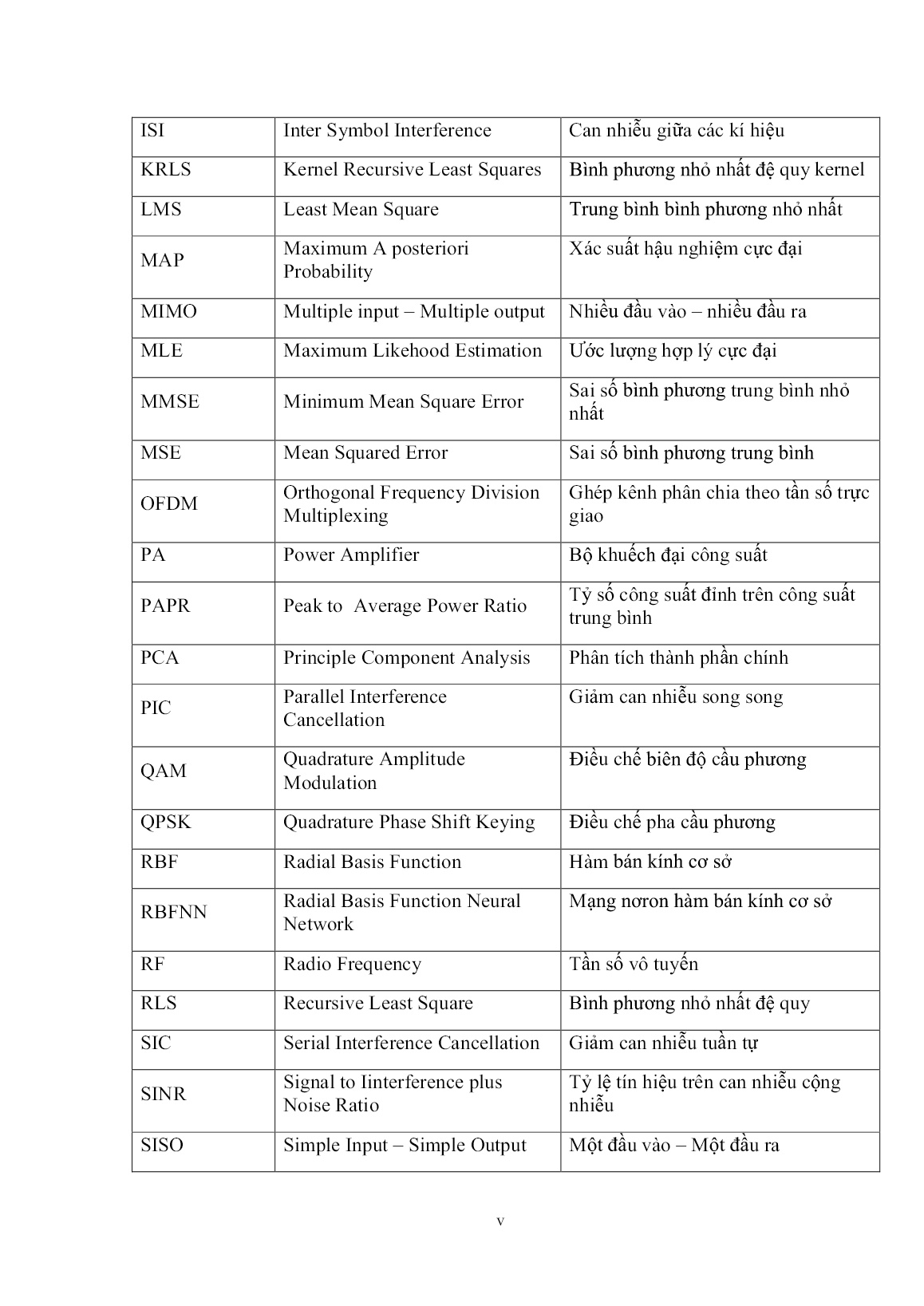
 các nghiên cứu [4,60] đã chứng minh rằng khi số sóng 
mang con K lớn , do định lý giới hạn trung tâm nên ICI có thể được coi như một quá 
trình ngẫu nhiên Gauss trắng. 
Vì vậy, phương trình (2.1) có thể được viết lại thành: 
 _p ICIp diag p p X H S J (2.53) 
Trong đó : 
1
_
0
( , ) ( ) ( )
K
p ICI
q
q k
pK k k q pK q pK k
 J H S Z (2.54) 
Có thể thấy rằng vì cả ICI và nhiễu cộng đều là những quá trình Gauss trắng nên 
 pJ là một quá trình Gauss trắng. 
Từ đây, có thể nhận thấy rằng bằng ICA, chúng ta có thể thu được được ước lượng 
ban đầu của pS là 0 pS và từ đó ước lượng ma trận đường chéo _p ICIdiagH 
của ma trận đáp ứng tần số _p ICIH . Theo nguyên lý của phương pháp lặp như đã nêu 
ở trên, từ đây chúng ta có thể giảm được ICI bằng cách giảm song song hoặc nối tiếp. 
2. 4 XÂY DỰNG MÔ HÌNH MÁY THU MIMO-OFDM DỰA TRÊN ICA 
Với các phân tích đã nêu ở trên, để thực hiện được giải pháp giảm ICI dựa trên ICA 
và phương pháp lặp, trước hết phải thiết kế được máy thu MIMO-OFDM có chứa bộ 
tách trộn, mỗi bộ có rM đầu vào và tM đầu ra. Ta gọi máy thu như thế là máy thu 
dựa trên ICA. Để xây dựng máy thu này, luận án sử dụng kết quả nghiên cứu [82] về 
máy thu MIMO dựa trên ICA. Trên cơ sở máy thu MIMO dựa trên ICA, luận án đề 
xuất máy thu MIMO-OFDM dựa trên ICA để sử dụng cho giải pháp giảm ICI. 
 52 
2.4.1 Máy thu MIMO dựa trên ICA 
Xem xét một hệ thống MIMO không dây với tM anten phát và rM anten thu được 
mô tả tại Hình 2.4. 
Hình 2.4: Mô hình hệ thống MIMO với máy thu dựa trên ICA 
Dòng dữ liệu nối tiếp được chia vào tM dòng dữ liệu song song, dữ liệu được điều 
chế QPSK và được tổ chức dưới dạng các khung gồm sN ký tự để truyền đi. Đáp ứng 
xung của kênh giữ không đổi trong khoảng thời gian của một khung và sẽ thay đổi từ 
khung này sang khung khác. Giả thiết rằng đồng bộ giữa bên phát và bên thu là hoàn 
hảo. Các ký tự thu được là: 
 1 2, , , , ,..., ,r
T
Mn p x n p x n p x n p x (2.55) 
Trong đó, ,jx n p là tín hiệu thu được tại thời điểm thứ n của ký tự thứ p tại anten 
thu thứ j; 1,2,..., ; 1,2,...,s rp N j M 
Phương trình biểu diễn ,k ix như sau: 
ICA 
 1 ,s n p 
DỊCH PHA SẮP XẾP LẠI 
QUYẾT ĐỊNH 
 ,
tM
s n p 
 1 ,x n p 
 ,n ps ,n ps 
ˆ ,n pd
 ,n pd
CÂN BẰNG ICA 
TIỀN MÃ HÓA 
GIẢI MÃ 
 ,n pd
 ,n pd 
 ,
rM
x n p
 53 
1,1 1,2 1, 1
,1 ,2 ,
, , ,
,
 ,
,
t
r r r t t
M
M M M M M
n p n n p n p
h l h l h l s n p
n p
h l h l h l s n p
x h s n
n
 (2.56) 
Trong đó ,n ps có kích thước t sM N và ,n px có kích thước r sM N là các 
tín hiệu phức băng gốc tương đương, nh có kích thước r tM M là đáp ứng xung 
của kênh pha đing phẳng. Các phần tử của nh có giá trị phức có phân phối là i.i.d . 
 ,n pn có kích thước là r sM N là nhiễu cộng Gauss trắng có giá trị trung bình 0 và 
phương sai là 
21
2
n . 
Dữ liệu gốc trước khi phát đi sẽ được tiền mã hóa bằng cách thêm vào một dữ liệu 
tham chiếu như sau: 
2
1
, , ,
1
refn p n p a n p
a
s d d (2.57) 
Trong đó, ,ref n pd là dữ liệu tham chiếu mà cả bên phát và bên thu đã được biết 
trước. Dữ liệu tham chiếu này được lựa chọn một cách ngẫu nhiên, có kích thước và 
cấu trúc giống như dữ liệu nguồn, các thành phần của ,ref n pd là độc lập với nhau; 
a là một hằng số tiền mã hóa với 0 1a . 
Trong mô hình máy thu MIMO dựa trên ICA được trình bày tại Hình 2.4, ngoài các 
khối giải mã và quyết định, còn có ba khối khác là khối ICA, khối dịch pha và khối 
sắp xếp lại. Các khối này được xây dựng để thực hiện ICA và khắc phục các nhược 
điểm của ICA là nhập nhằng về tính hoán vị và nhập nhằng về nhân vô hướng. Hoạt 
động của các khối này được mô tả như sau: 
Khối ICA 
Khối ICA thực hiện tách dữ liệu gốc từ một trộn tuyến tính dựa trên số liệu thống kê 
của các ký tự thu nhận được. Để làm được điều này khi không biết thông tin trạng 
thái của kênh thì cần phải đáp ứng được các giả định sau đây: 
1. Các dữ liệu nguồn phải độc lập thống kê. 
2. Dữ liệu nguồn phải có phân phối phi Gauss (tức là không có phân phối Gauss) 
3. Dữ liệu nguồn có trung bình bằng 0. 
 54 
4. Số anten thu phải lớn hơn hoặc bằng số anten phát. 
Để thực hiện tách trộn, trước hết làm trắng (whitening) vectơ tín hiệu thu được 
 ,n px để nhận được một vectơ mới là ,n py mà các thành phần của nó là không 
tương quan với nhau. 
 , ,n p n n p y V x (2.58) 
Trong đó nV là ma trận làm trắng . 
Sao cho: 
 , ,
t
H
M
p
n p n p y y IE (2.59) 
Như mục (2.1.2) đã nêu, một cách thường được dùng để tìm ma trận làm trắng 
 nV là thực hiện phân rã trị riêng trên ma trận tự tương quan của ,n px là 
 xx nR . 
 x , ,Hx
i
n n p n p R x xE 
Khi đó, nV được xác định như sau : 
1/2 T
n n n n
 V E D E (2.60) 
Trong đó, nE là ma trận của các vectơ riêng (eigenvector) của xx nR , 
 nD là ma trận đường chéo của các trị riêng (eigenvalue) của xx nR . 
Tín hiệu thu được sau khi đã được làm trắng sẽ được đưa đến bộ tách các thành phần 
độc lập để nhận được ước lượng của tín hiệu đã phát đi: 
 , , ,n p n n p n n n p s W y W V s (2.61) 
Tuy nhiên, do tính chất nhập nhằng của ICA, ,n ps có thể có thứ tự và pha khác 
với tín hiệu phát ,n ps ban đầu. Điều này có thể biểu diễn bằng biểu thức sau: 
 , ,n p n n n p s D P s (2.62) 
Trong đó, ma trận đường chéo nD thể hiện cho sự nhập nhằng về pha và ma trận 
 nP thể hiện cho sự nhập nhằng về tính hoán vị. 
 55 
Các khối dịch pha và khối sắp xếp lại sẽ xử lý tiếp các nhập nhằng này. 
Khối dịch pha 
Nhập nhằng về pha có thể giải quyết bằng cách quay vectơ tín hiệu ,k ps . 
, , ii i
i
n
s n p s n p
n
 (2.63) 
Trong đó, 1,2,..., ti M là chỉ số anten phát. 
 i n là ước lượng độ dịch pha tại anten thứ i, với điều chế QPSK thì i n xác 
định bởi : 
1
44,
j
i i
p
n s n p e
 
 
 
E (2.64) 
Tuy nhiên, biểu thức (2.64) lại đưa ra một nhập nhằng về góc quay pha  đối với 
 ,is n p . Đối với điều chế QPSK thì 
3
0, , ,
2 2
 
 
 
 
. Nhập nhằng này có thể 
được giải quyết cùng với việc giải quyết nhập nhằng về tính hoán vị bằng khối sắp 
xếp lại như sẽ trình bày tiếp theo sau đây: 
Khối xắp xếp lại 
Tiền mã hóa tại (2.57) đã làm cho các dữ liệu được phát đi có tương quan với dữ liệu 
tham chiếu. Việc sắp xếp lại thứ tự các dữ liệu nhận được sẽ được thực hiện bằng 
cách tìm ra một cách sắp xếp k của tM dòng dữ liệu nguồn (tương ứng với tM 
anten) sao cho với cách sắp xếp này thì giá trị tuyệt đối của ước lượng tương quan 
chéo , ,i n giữa các dòng dữ liệu dò được với dữ liệu tham chiếu là lớn nhất. 
Giả thiết rằng dịch pha (2.63) là hoàn hảo, tương quan chéo , ,i n được xác định 
như sau: 
 
  
*
,
* *
, ,,2
, , , ,
1
, , , ,
1
ref ii
p
ref i ref ii ref i
p p
i n s n p d n p
d n p d n p a d n p d n p
a
E
E E
(2.65) 
Trong đó, 
1
, , ,ref refn p n k n p 
 d D P d là 
 56 
Vì tính chất độc lập với nhau giữa dữ liệu nguồn và dữ liệu tham chiếu, cũng như 
tính độc lập với nhau giữa các tín hiệu nguồn tại các dòng tín hiệu khác nhau, nên 
chúng ta có thể viết: 
 
*
,, , 0ref ii
p
d n p d n p
 E (2.66) 
 
*
,,
1 
, , 
0 
ref iref i
p
khi i i
d n p d n p
khi i i
E (2.67) 
Từ (2.57), giá trị tuyệt đối của tương quan chéo (2.65) khi sắp xếp thứ tự đúng sẽ là: 
2
, ,
1
a
i n
a
 (2.68) 
Nếu không đúng thì: 
 , , 0i n (2.69) 
Vì vậy, cách sắp xếp lại thứ tự đúng là cách sắp xếp sao cho , ,i n đạt giá trị 
lớn nhất. Tức là: 
1
arg max , ,
tM
i
k i n
  (2.70) 
Ước lượng của dữ liệu ˆ ,n pd sau khi sắp xếp lại sẽ là: 
 1ˆ , , ,..., ,k k t
T
M
n p k d n p d n p
d D (2.71) 
Trong đó, ma trận đường chéo kD được xác định bởi: 
/4 /4, ,
, ,
j ji nn diag je sign e
i n
D (2.72) 
Trong đó, .sign là hàm dấu. 
Ma trận kD được đưa ra để giải quyết quyết nhập nhằng góc quay pha  như đã 
nêu ở trên. 
Cuối cùng, ước lượng mềm của dữ liệu nguồn nhận được bằng cách giải mã: 
 57 
 2 ,, 1 , ,i i ref id n p a s n p ad n p (2.73) 
Ước lượng mềm này được đưa tới bộ quyết định để nhận được ước lượng cứng 
 ,id n p của dữ liệu nguồn ,id n p . 
2.4.2 Mô hình máy thu MIMO-OFDM có cân bằng ICA 
Mô hình máy thu MIMO-OFDM có thể được suy ra một cách trực tiếp từ máy thu 
MIMO dựa trên ICA kế thừa kết quả của [82] như đã nêu ở trên bằng cách sử dụng K 
bộ cân bằng ICA như được trình bày tại Hình 2.5 . 
Chọn dữ liệu tại một sóng mang con nào đó làm dữ liệu tham chiếu, ký hiệu sóng 
mang con đó là rk . 
Ký hiệu pK k d là vectơ tín hiệu nguồn tại sóng mang con thứ k và được định 
nghĩa như sau: 
 1 2, ,..., t
T
MpK k d pK k d pK k d pK k d (2.74) 
Trong đó, id pK k là tín hiệu nguồn của ký tự thứ p tại sóng mang con thứ k ở 
anten thứ i. 
Tín hiệu nguồn này sẽ được tiền mã hóa để tạo thành tín hiệu phát đi tương tự như 
(2.57) như sau: 
2
1
1
i i i rS pK k d pK k ad pK k
a
 (2.75) 
Trong đó: 
 iS pK k là tín hiệu tại sóng mang con thứ k ( rk k ) của ký tự OFDM thứ p tại 
anten thứ i như đã định nghĩa tại chương 1. 
rk là sóng mang con tham chiếu. 
a với 0 1a là hằng số tiền mã hóa. 
Lưu ý rằng, riêng tín hiệu nguồn tại sóng mang con tham chiếu không được tiền mã 
hóa, tức là: 
 i r i rS pK k d pK k 
 58 
a) Máy phát 
b) Máy thu 
Hình 2.5: Sơ đồ hệ thống MIMO-OFDM với máy thu ICA 
Tiền mã hóa tạo ra một tương quan giữa dữ liệu tại sóng mang con rk và dữ liệu tại 
1K sóng mang con còn lại. 
Đối với mỗi sóng mang con, chúng ta sử dụng một bộ cân bằng ICA có cấu trúc 
tương tự như bộ cân bằng ICA của máy thu MIMO [82] đã nêu ở trên. Trong K bộ 
cân bằng ICA này, có một bộ cân bằng dành cho sóng mang con tham chiếu và 1K 
bộ cân bằng cho các sóng mang con còn lại. Các bộ cân bằng ICA này được mô tả tại 
các Hình 2.6 và Hình 2.7 sau đây. Trong đó Hình 2.6 mô tả bộ cân bằng ICA cho 
 1 ,s k p
TIỀN MÃ HÓA 
IFFT 
 ,k id 
ĐIỀU CHẾ 
CHÈN CP P/S 
P/S 
 ,
rM
s k p 
IFFT CHÈN CP 
FFT 
FFT 
CÂN BẰNG ICA 
GIẢI MÃ 
 1 1X K 
GỠ BỎ CP 
GỠ BỎ CP 
S/P 
S/P 
CÂN BẰNG ICA 
CÂN BẰNG ICA 
QUYẾT ĐỊNH 
 1 0X 
 0
rM
X 
 1
rM
X K 
 59 
sóng mang con tham chiếu 
rk và Hình 2.7 mô tả bộ cân bằng ICA cho các sóng 
mang con còn lại. 
Hình 2.6: Bộ cân bằng ICA cho sóng mang con tham chiếu rk 
Hình 2.7: Bộ cân bằng ICA cho sóng mang con rk k k 
Về bản chất, bộ cân bằng ICA cho sóng mang con tham chiếu rk không khác gì so 
với bộ cân bằng ICA cho các sóng mang con khác, chỉ lưu ý rằng, vì dữ liệu tại sóng 
mang con tham chiếu không được tiền mã hóa, nên ước lượng tín hiệu ˆ rpK k S 
cũng chính là ước lượng của tín hiệu gốc ˆ rpK k d . 
Hoạt động của mỗi bộ cân bằng ICA này cũng tương tự như bộ cân bằng ICA của 
máy thu MIMO [82] đã nêu ở trên. Có thể mô tả tóm tắt lại như sau (ở đây chúng ta 
trình bày chung cho cả hai trường hợp) : 
ICA DỊCH PHA SẮP XẾP LẠI 
 1 rX pK k 
 rpK k S
rM r
X pK k 
 rpK k S 
ˆ
rpK k S 
ICA DỊCH PHA SẮP XẾP LẠI 
 1X pK k 
 pK k S
rM
X pK k 
 pK k S 
ˆ pK k d 
 60 
Đầu tiên, làm trắng vectơ tín hiệu pK k X bằng ma trận làm trắng pK k V để 
nhận được một vectơ mới là pK k Y mà các thành phần của nó là không tương 
quan với nhau: 
 pK k pK k pK k Y V X (2.76) 
Bước tiếp theo tìm ma trận trực giao pK k G sao cho ma trận tách để tách trộn 
 pK k pK k pK k W G V có thể tách trộn các tín hiệu: 
 pK k pK k pK k S W X (2.77) 
Xây dựng thuật toán phù hợp để tìm ma trận pK k W là một bài toán đặt ra để có 
thể thực hiện được giải pháp giảm ICI bằng ICA. Việc giải quyết bài toán này sẽ 
được trình bày trong phần tiếp theo của luận án. 
Vectơ tín hiệu pK k S sẽ tiếp tục được xử lý các nhập nhằng về pha và tính hoán 
vị như trong [82] và sau đó nhận được ước lượng của tín hiệu gốc phát đi trên sóng 
mang con k là ˆ rpK k d ( Đối với sóng mang con tham chiếu rk thì cũng chính là 
 ˆ rpK k S vì tại sóng mang con tham chiếu, tín hiệu gốc không được tiền mã hóa). 
Vì dữ liệu tại các sóng mang con khác nhau có cùng một tham chiếu nên nhập nhằng 
về pha và nhập nhằng về tính hoán vị được xử lý cùng một cách với sóng mang con 
tham chiếu. Do đó, sau các bộ cân bằng ICI, tín hiệu tại các sóng mang con sẽ có 
cùng thứ tự và góc quay pha giống nhau. Nói cách khác, bằng cách sử dụng một 
sóng mang con tham chiếu, chúng ta sẽ xử lý được nhập nhằng của ICA cho tất cả 
các sóng mang con. 
Tuy nhiên, cách sử dụng bộ cân bằng ICA cho từng sóng mang con, trong đó có một 
sóng mang con tham chiếu để xử lý nhập nhằng của ICA có một nhược điểm cơ bản 
là không phù hợp với kênh pha đing lựa chọn tần số [39]. Sở dĩ có vấn đề này là do 
khi kênh là pha đing lựa chọn tần số, một số sóng mang con sẽ chịu tác động của pha 
đing, tín hiệu tại các sóng mang con đó sẽ bị méo. Hậu quả là tính độc lập của các tín 
hiệu tại các sóng mang con đó bị phá vỡ. Trong trường này, việc sử dụng bộ cân 
bằng ICA để tách trộn các thành phần độc lập như trình bày ở trên cho các kênh bị 
pha đing là không hiệu quả và không phục hồi được tín hiệu ban đầu đã phát đi. Để 
khắc phục điểm yếu này, luận án đề xuất một giải pháp có tính ổn định, tin cậy hơn, 
đó là chỉ sử dụng một bộ cân bằng ICA cho một sóng mang con, còn các bộ cân bằng 
khác là cân bằng theo thuật toán sai số bình phương trung bình nhỏ nhất (Minimum 
mean square error-MMSE) , được gọi là cân bằng MMSE, như sẽ được trình bày 
trong phần tiếp sau đây. 
 61 
2.4.3 Mô hình máy thu MIMO-OFDM có cân bằng ICA-MMSE 
Mô hình may thu có cân bằng ICA-MMSE được trình bày trong Hình 2.8. Trong mô 
hình này, chúng ta chỉ giữ lại một bộ cân bằng ICA cho sóng mang con tham chiếu 
rk , còn đối với các sóng mang con khác, sử dụng cân bằng MMSE để tách trộn các 
tín hiệu. Chúng ta cũng sẽ chứng minh rằng mô hình này sẽ giải quyết nhập nhằng về 
tính hoán vị và pha cho tất cả các sóng mang con. 
Hình 2.8: Mô hình máy thu MIMO-OFDM với cân bằng ICA-MMSE 
Chúng ta sẽ lần lượt xem xét lần lượt các thành phần của mô hình này. 
Bộ cân bằng ICA 
Trong mô hình máy thu có cân bằng ICA-MMSE, bộ cân bằng ICA cho sóng mang 
con tham chiếu rk (Hình 2.8 mô tả trong trường hợp chúng ta chọn 0rk , tuy nhiên 
trong trường hợp tổng quát, rk có thể là bất kỳ một sóng mang con nào) cũng giống 
như bộ cân bằng ICA cho sóng mang con tham chiếu đã trình bày tại Hình 2.6. Cách 
thức hoạt động của bộ cân bằng ICA đã được trình bày phía trên và không cần phải 
nhắc lại ở đây. 
Bộ cân bằng MMSE 
Mô hình máy thu có cân bằng ICA-MMSE tại Hình 2.8 được vẽ lại một cách tổng 
quát dưới dạng sơ đồ khối như Hình 2.9. 
 ˆ 1K d
FFT 
FFT 
CÂN BẰNG ICA 
GIẢI MÃ 
 1 0X 
 1 1X K 
 0
rM
X
 1
rM
X K 
GỠ BỎ CP 
GỠ BỎ CP 
S/P 
S/P 
MMSE 
MMSE 
 ˆ 0d 
 ˆ 0S 
QUYẾT 
ĐỊNH 
 62 
Hình 2.9: Sơ đồ khối máy thu ICA-MMSE 
Các ma trận tách tín hiệu pK k W đối với các sóng mang con k khác với sóng 
mang con tham chiếu 0,1,... 1 \ rk K k sẽ xác định bằng MMSE có sử dụng cấu 
trúc tương quan tín hiệu như đã trình bày tại (2.75). 
Sơ đồ MMSE [28] cho sóng mang con k được trình bày tại Hình 2.10 
Hình 2.10: Sơ đồ MMSE cho sóng mang con k 
Khi ma trận cân bằng của khối MMSE là pK k W thì ước lượng ˆ pK k S của 
 pK k S được xác định bởi : 
 ˆ pK k pK k pK k S W X (2.78) 
Định nghĩa vectơ lỗi tại sóng mang con k như sau: 
 ˆ ˆ rpK k pK k pK k e S S (2.79) 
Phương pháp MMSE [28] là tìm SMM E pK k W sao cho: 
CÂN BẰNG ICA 
MMSE 
GIẢI MÃ 
 rpK k X 
 pK k X 
 0,1,..., 1 \ rk K k 
 ˆ rpK k S 
 ˆ pK k S 
 ˆ pK k d 
 0,1,..., 1k K 
 ˆ pK k S 
 pK k X 
 ˆ rpK k pK k e S S ˆ rpK k S
 
- 
+ 
 pK k W 

 
 63 
 
2
S
ˆ ˆarg min MM E r
pK k
pK k pK k pK k
W
W S SE (2.80) 
Khi đó, SMM E pK k W được xác định như sau[2]: 
 1S ,
H
MM E rpK k k k k
XS XX
W R R (2.81) 
Trong đó, kXXR là ma trận tự tương quan của pK k X và , rk kXSR là ma trận 
tương quan chéo giữa pK k X và ˆ rpK k S , là một hằng số sẽ được đề cập 
đến sau đây. 
 
 ˆ,
H
p
H
r r
p
k pK k pK k
k k pK k pK k
XX
XS
R X X
R X S
E
E
 (2.82) 
Sau đây,luận án chứng minh rằng cân bằng MMSE cho sóng mang con k có ma trận 
cân bằng được xác định tại (2.81) sẽ tách trộn được tín hiệu tại sóng mang con thứ k 
với cùng thứ tự và pha như sóng mang con tham chiếu rk nếu như hằng số  được 
lựa chọn một cách phù hợp. 
Chứng minh: 
Từ phương trình (2.52) và giải thiết rằng nhiễu cộng Gauss không đáng kể, ta có 
phương trình trộn tín hiệu tại sóng mang con k là: 
 ,ppK k k k pK k X H S (2.83) 
Từ phương trình (2.83) và (2.77), ta có thể biểu diễn lại các ma trận tương quan 
 , rk kXSR và s kR như sau: 
Đối với , rk kXSR , ta có: 
 
ˆ,
, ,
H
r r
p
H
p S r r
k k pK k pK k
k k k k pK k
XSR X S
H R W
E
 (2.84) 
Trong đó ,S rk kR là ma trận tương quan chéo giữa pK k S và ˆ rpK k S 
 ˆ,
H
S r r
p
k k pK k pK k R S SE (2.85) 
Tương quan chéo giữa tín hiệu iS pK k và ˆi rS pK k là: 
 64 
 
*
*
2
* *
2 2
ˆ
1 ˆ
1
1 ˆ ˆ
1 1
i i r
p
i i r i r
p
i i r i r i r
p
S pK k S pK k
d pK k ad pK k d pK k
a
a
d pK k d pK k d pK k d pK k
a a
 
  
 
  
E
E
E
 (2.86) 
Nếu cân bằng ICA cho sóng mang con tham chiếu là hoàn hảo, tức là 
 ˆi r i rd pK k d pK k , và vì các tín hiệu được coi là độc lập với nhau nên từ 
công thức trên, ta có: 
  
**
2
ˆˆ
1
i i r i r i r
p p
a
S pK k S pK k d pK k d pK k
a
E E 
 (2.87) 
Giả thiết rằng 2 1i
p
d pK k E từ biểu thức trên , thu được: 
 *
21
i i r
p
a
S pK k S pK k
a
E (2.88) 
Tương quan chéo giữa tín hiệu jS pK k và i rS pK k với j i là: 
 
*
*
2
* *
2 2
1
1
1
1 1
0
j i r
p
j j r i r
p
j i r j r i r
p
S pK k S pK k
d pK k ad pK k d pK k
a
a
d pK k d pK k d pK k d pK k
a a
 
  
 
 
  
 
E
E
E
Vì vậy ,S rk kR là một ma trận đường chéo kích thước t tM M với các giá trị nằm 
trên đường chéo là 
21
a
a 
: 
2
,
1
tS r M
a
k k
a
R I (2.89) 
 65 
Tương tự như vậy, kXXR có thể biểu diễn như sau : 
 , ,
H
p s pk k k k k k XXR H R H 
Trong đó là ma trận tự tương quan của pK k S 
 
t
H
s
p
M
k pK k pK k 
R S S
I
E
 (2.90) 
Thay (2.89) và (2.90) vào (2.81), ta có : 
1
S
1
1
2
, , , ,
, ,
,
1
t
H H
H
MM E p S r r p s p
H H
p r r
p r M
pK k k k k k pK k k k k k k
k k pK k k k k
a
k k pK k
a



S S
W H R W H R H
H W R R
H W I
 (2.91) 
Vì vậy, nếu chọn 
21 a
a

 thì ta có : 
1
S , tMM E p r MpK k k k pK k
 W H W I (2.92) 
Khi đó : 
 S tMM E r MpK k pK k pK k pK k W X S W I (2.93) 
Điều này có nghĩa rằng MMSE sẽ tách trộn được tín hiệu tại sóng mang con thứ k 
với thứ tự và pha giống như tại sóng mang con tham chiếu rk . 
Như vậy mô hình với một bộ cân bằng ICA cho sóng mang con tham chiếu và các bộ 
cân bằng MMSE cho các sóng mang con còn lại đảm bảo tách trộn tín hiệu tại tất cả 
các sóng mang con với cùng một thứ tự và độ dịch pha. 
Giải mã 
Sau khi tách trộn, ước lượng mềm ˆ pK k S sẽ được giải mã để nhận pK k d 
được xác định bởi : 
 2 ˆ ˆ1i i i rd pK k a S pK k aS pK k (2.94) 
 66 
Lưu ý rằng dữ liệu tại sóng mang con tham chiếu không được tiền mã hóa, tức là: 
 ˆi r i rd pK k S pK k 
 pK k d sau đó được đưa qua bộ quyết định để nhận được ước lượng cứng 
 pK k d được định nghĩa bởi: 
 1 2, ,..., tMpK k d pK k d pK k d pK k d (2.95) 
với id pK k được xác định bởi: 
 i i id pK k Q d pK k (2.96) 
Trong đó  .Q là hàm ước lượng cứng của dữ liệu. Để giải mã, sóng mang con tham 
chiếu rk cần được giải mã trước. 
2. 5 XÂY DỰNG THUẬT TOÁN CHO BỘ CÂN BẰNG ICA 
Để thực hiện được giải pháp cân bằng dựa trên ICA cần có thuật toán ICA hiệu quả. 
Đã có rất nhiều công trình nghiên cứu về các thuật toán ICA và số các thuật toán 
được phát triển là rất phong phú[26,38,52]. Tuy vậy, hầu hết các thuật toán này tập 
trung vào trường hợp trộn không có nhiễu hoặc được coi là không đáng kể. Hệ trộn 
như vậy được biểu diễn bởi phương trình = ( )n nx As với ( )ns là vectơ tín hiệu 
nguồn và A là ma trận trộn. 
Tuy nhiên, trong mô hình giải pháp mà luận án đề xuất thì can nhiễu giữa các sóng 
mang con được xem xét như một quá trình Gauss và tạo thành nhiễu cộng Gauss. D