Luận án Khung cộng tác đa dụng trong môi trường tính toán lưới

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
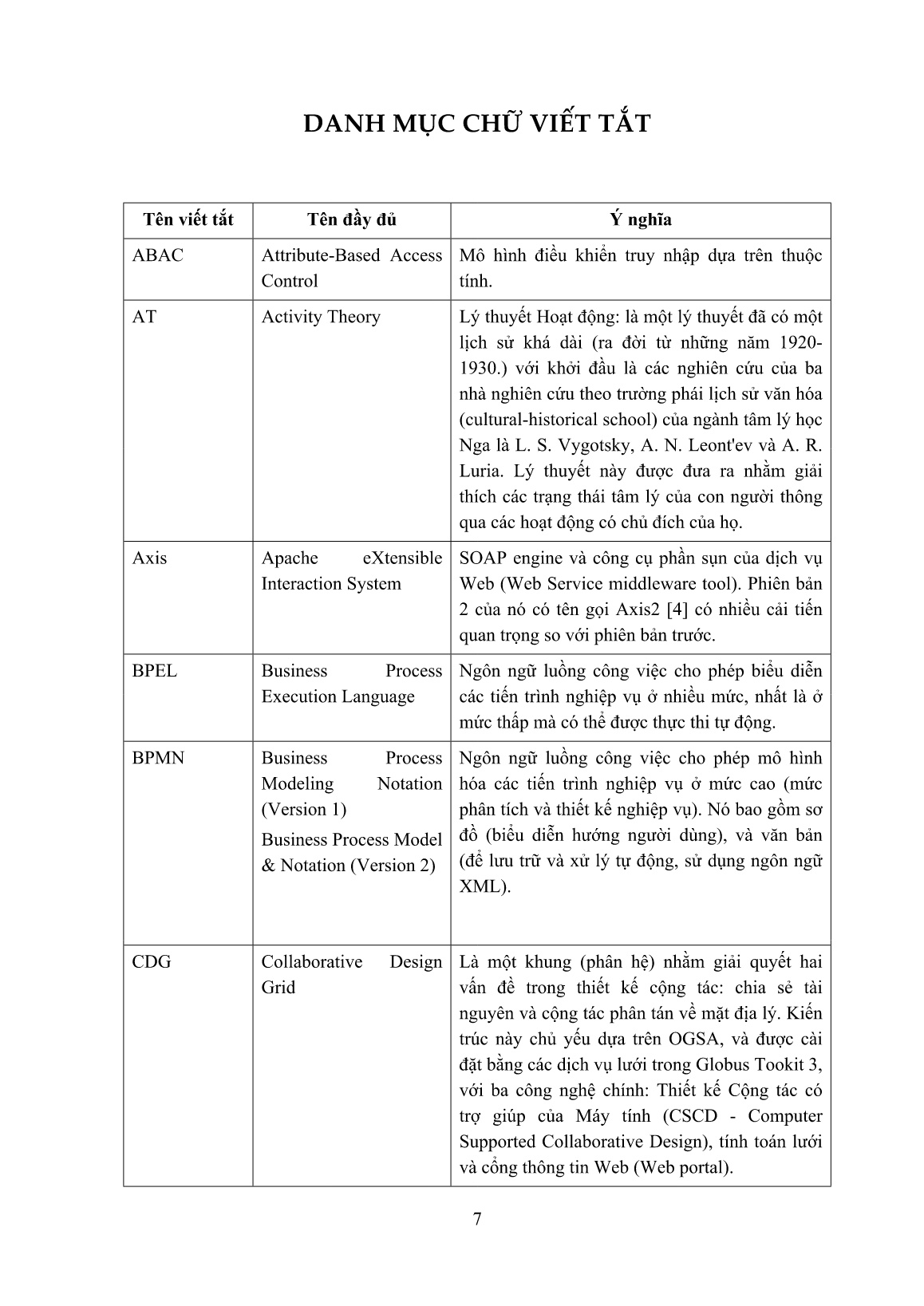
Trang 7
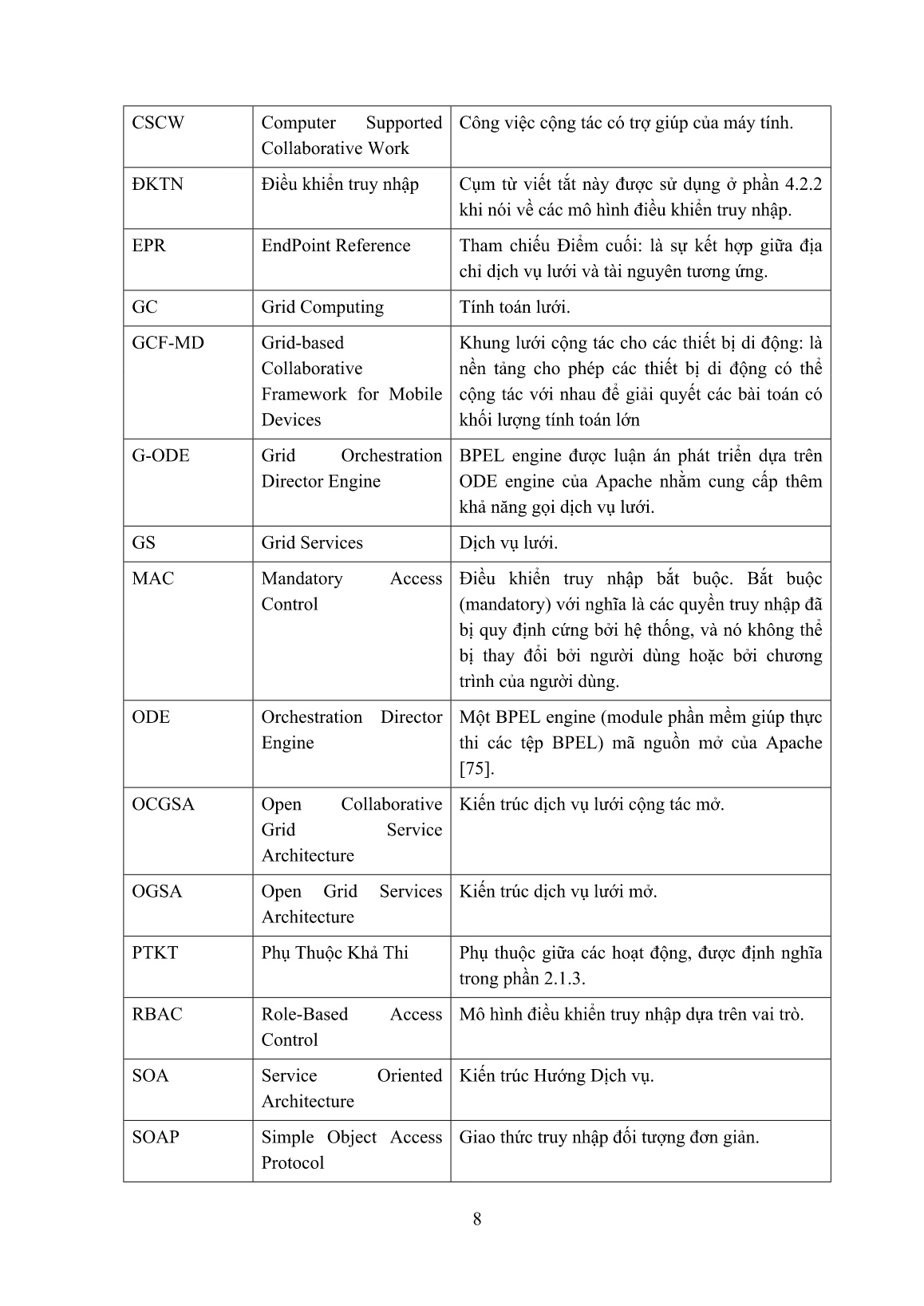
Trang 8
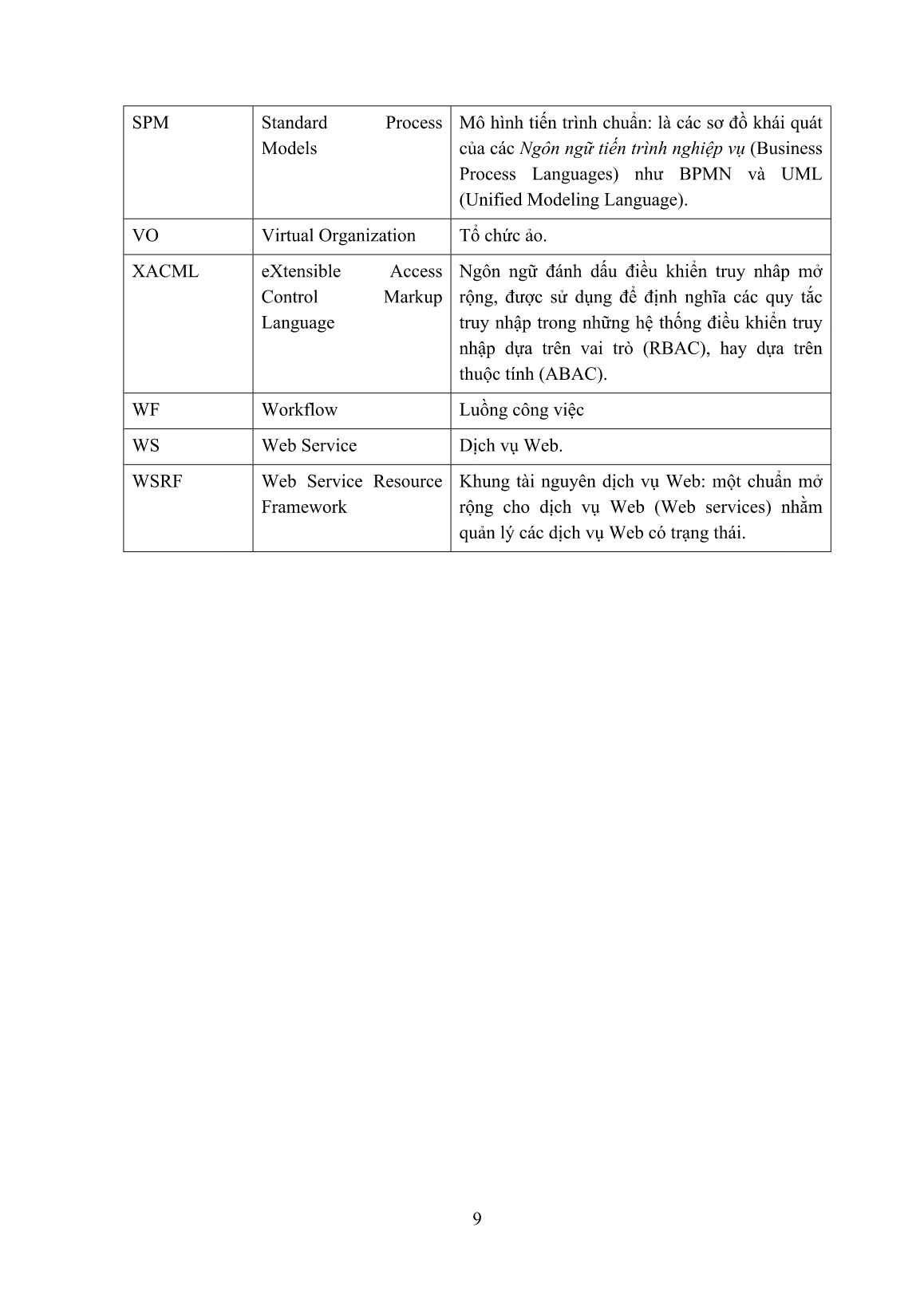
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Luận án Khung cộng tác đa dụng trong môi trường tính toán lưới", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Luận án Khung cộng tác đa dụng trong môi trường tính toán lưới

tiết hóa đã trình bày ở trên, có thể nhận thấy giữa chúng có một số quan hệ như sau: Các phép tách giúp tăng cường tính khả thi của hoạt động: tức là nếu A là hoạt động chưa khả thi thì decomposition(A) có thể khả thi. Điều này có nghĩa là decomposition(A) ® A. Đồng thời, do phép tách là phép biến đổi tương đương về chức năng, nên nếu decomposition(A) không khả thi, thì khả năng A là không khả thi cũng rất lớn. Các phép bổ sung (ngoại trừ bổ sung hoạt động), đều tạo ra hoạt động mới, cho phép xác định khả thi hoạt động cũ. Tức là, nếu A’ = A + d thì A’ ® A; Tăng cường tính khả thi của hoạt động Phần này sẽ trình bày về cách tiếp cận thứ hai giúp tăng cường tính khả thi của kế hoạch. Khác với cách tiếp cận đầu tiên (tìm và bổ sung thêm các hoạt động mới vào bản kế hoạch), cách tiếp cận này lại tìm cách tăng cường tính khả thi của một trong các loại hoạt động hiện có trong kế hoạch, hoạt động tập thể, bằng cách chuyển đổi cách biểu diễn của nó từ ngôn ngữ luồng hướng đồ thị BPMN sang ngôn ngữ luồng có cấu trúc và tính thực thi cao hơn là BPEL. Các kỹ thuật chuyển đổi Trong thời gian gần đây, vấn đề chuyển đổi giữa hai loại ngôn ngữ luồng công việc là ngôn ngữ hướng đồ thị và ngôn ngữ hướng cấu trúc (với hai ngôn ngữ tiêu biểu là BPMN và BPEL) thu hút được khá nhiều sự chú ý của các nhà nghiên cứu, bởi một số lý do như sau: Nhu cầu của các phương pháp phát triển hệ thống hướng tiến trình hoàn chỉnh [73]: Tương tự như các phương pháp phát triển phần mềm khác, phương pháp này cũng chia quá trình phát triển phần mềm thành một số giai đoạn tiêu biểu như: phân tích, thiết kế và cài đặt. Ở giai đoạn phân tích và thiết kế, các hoạt động nghiệp vụ trong doanh nghiệp được biểu diễn dưới dạng các mô hình tiến trình nghiệp vụ (business process models). Do các mô hình này chủ yếu dành cho việc trao đổi ở mức cao giữa những nhà phân tích và thiết kế, nên cách biểu diễn phù hợp nhất là bằng các ngôn ngữ hướng đồ thị hay biểu đồ. Trong số các ngôn ngữ loại này, BPMN nổi lên như một ngôn ngữ tiêu chuẩn đang được sử dụng rộng rãi và được hỗ trợ bởi khá nhiều công cụ (khoảng 40 công cụ cho đến nay [100]). Trái lại ở giai đoạn cài đặt, lại đòi hỏi các các công cụ thích hợp để biểu diễn các tiến trình nghiệp vụ mà có thể thực thi được. So với các mô hình nghiệp vụ ở các giai đoạn phân tích và thiết kế, mô hình nghiệp vụ có thể thực thi được ở giai đoạn cài đặt cần bổ sung thêm nhiều chi tiết cài đặt như: thao tác dữ liệu, liên kết ứng dụng,v.v. Ngôn ngữ thích hợp để biểu diễn các ngiệp vụ có thể thực thi được thường là các ngôn ngữ có cấu trúc, trong đó BPEL là ngôn ngữ tiêu biểu. Do đó, việc phát triển các kỹ thuật chuyển đổi tự động hay bán tự động từ các ngôn ngữ hướng đồ thị sang ngôn ngữ có cấu trúc là một nhu cầu tự nhiên và cần thiết. Cho phép các tiến trình nghiệp vụ thực thi được trong một môi trường tính toán đích: Một số ngôn ngữ luồng công việc hỗ trợ việc thực thi các tiến trình nghiệp vụ trong một số môi trường cụ thể nào đó. Ví dụ như BPEL hỗ trợ trực tiếp việc kết hợp (composition) và gọi các dịch vụ Web (Web service). Ngoài ra, gần đây có một số mở rộng của BPEL cho phép việc gọi các dịch vụ lưới (Grid service) [71] [95] [9]. Tuy nhiên, các tiến trình nghiệp vụ, được biểu diễn bằng các ngôn ngữ ở mức thực thi này thường không dễ nhìn và dễ hiểu với con người, do chứa nhiều chi tiết phức tạp liên quan đến việc gọi và thực thi các dịch vụ bên ngoài. Do đó, đứng ở góc độ người dùng, mong muốn biểu diễn các tiến trình nghiệp vụ bằng các ngôn ngữ hướng đồ thị và sau đó các tiến trình này có thể được dịch tự động sang ngôn ngữ ở mức thực thi được. Trong phần này, chúng ta sẽ điểm lại các kỹ thuật chính hiện nay được dùng để dịch từ ngôn ngữ hướng đồ thị sang ngôn ngữ có cấu trúc nói chung và từ ngôn ngữ BPMN sang BPEL nói riêng, nhằm làm sáng tỏ các ưu điểm và hạn chế của những kỹ thuật này. Do sự không khớp nhau của hai lớp ngôn ngữ, như đã được chỉ ra trong [79], nên vấn đề chuyển đổi giữa chúng không hề đơn giản. Hơn nữa, khi mục đích chuyển đổi khác nhau cũng đòi hỏi phải có các kỹ thuật khác nhau. Điều này càng làm cho vấn đề chuyển đổi thêm khó khăn và phức tạp. Chính vì vậy, trong khuôn khổ nghiên cứu của luận án, sẽ không có tham vọng khảo sát toàn bộ các kỹ thuật này, mà chỉ tập trung vào một phía của việc chuyển đổi. Đó là chuyển đổi từ ngôn ngữ hướng đồ thị sang ngôn ngữ có cấu trúc. Trọng tâm nghiên cứu này cũng phù hợp với một trong những mục tiêu nghiên cứu của luận án, đó là tìm hiểu vấn đề chi tiết hóa kế hoạch. Còn ở chiều ngược lại, luận án dự định sẽ nghiên cứu trong tương lai gần. Mặc dù hiện nay có khá nhiều các kỹ thuật chuyển đổi từ ngôn ngữ hướng đồ thị sang ngôn ngữ có cấu trúc, chúng đều có chung một số mục tiêu như sau [3]: Đầy đủ (Completeness): làm sao cho kỹ thuật có thể được áp dụng cho bất kỳ topo (topology) nào của tiến trình nguồn (được biểu diễn bằng ngôn ngữ hướng đồ thị). Tự động (Automation): làm sao cho việc chuyển đổi có thể được tiến hành một cách tự động, không cần sự can thiệp của con người. Dễ đọc (Readability): làm sao để tiến trình được tạo ra ở ngôn ngữ đích là dễ đọc và dễ hiểu bởi con người. Vì thực tế cho thấy, dù mức độ tự động của chuyển đổi có tốt đến đâu thì vẫn cần sự can thiệp của con người đối với tiến trình đích. Do đó mục tiêu này nhằm giảm gánh nặng cho người dùng khi phải can thiệp vào tiến trình đích. Trong [65], một số chiến lược cho việc chuyển đổi giữa hai lớp ngôn ngữ đã được đề xuất (sử dụng hai ngôn ngữ BPMN và BPEL để minh họa cho các chiến lược). Trong số đó, có bốn chiến lược áp dụng cho việc chuyển đổi từ ngôn ngữ hướng đồ thị sang ngôn ngữ có cấu trúc: Bảo toàn các thành phần (Element-preservation): Ý tưởng chung của chiến lược là ánh xạ tất cả các thành phần của tiến trình nguồn sang cấu trúc Flow, và ánh xạ các cung (arcs) sang cấu trúc Link. Chiến lược này tuy đơn giản, nhưng còn tồn tại hai hạn chế đối với tiến trình đích được tạo ra: nó không dễ đọc và chứa nhiều thành phần activity rỗng (empty activities). Tối thiểu hóa các thành phần (Element-minimization): Chiến lược này nhằm khắc phục hạn chế thứ hai của chiến lược đầu tiên. Phát hiện các cấu trúc (Structure-identification): Chiến lược này nhằm khắc phục hạn chế đầu (tiến trình đích không dễ đọc) của chiến lược thứ nhất, bằng cách phát hiện các thành phần activity có cấu trúc trong tiến trình nguồn, để từ đó ánh xạ chúng sang các thành phần activity có cấu trúc trong tiến trình đích. Tối đa hóa các cấu trúc (Structure-maximization): Chiến lược này nhằm nâng cao chiến lược thứ ba bằng cách phát hiện tối đa các activity có cấu trúc trong tiến trình nguồn, từ đó giúp giảm thiểu số lượng các thành phần phải ánh xạ. Nó đồng nghĩa với việc tạo ra tiến trình đích đơn giản và dễ đọc hơn. Trong [70], việc chuyển đổi từ BPMN sang BPEL được gọi là ánh xạ (mapping), và được chia thành hai nhóm: Ánh xạ các thành phần cơ bản (Mappings of basic elements): Ở nhóm này, hầu như tất cả các thành phần cơ bản của BPMN (như tasks, sub-processes, activity loops, events, v.v) đều được ánh xạ sang các thành phần tương ứng của BPEL. Ánh xạ các khối cấu trúc (Mappings of Blocks): Một khối cấu trúc là một đồ thị con liên thông (sub connected graph) kết nối với phần còn lại của tiến trình nguồn (là một đồ thị) bởi đúng hai luồng tuần tự (sequence flows): một luồng vào và một luồng ra. Các khối cấu trúc có thể kết hợp với nhau để tạo thành khối cấu trúc lớn hơn. Khối cấu trúc lớn nhất được gọi là một phân cấp khối cấu trúc (block hierarchy) (xem Hình 3-1). Trong [49], một giải thuật tìm kiếm khối cấu trúc này với độ phức tạp tuyến tính đã được trình bày. Một khối cấu trúc có chứa một số cấu trúc được gọi là các mẫu (patterns), mà có thể được ánh xạ sang các thành phần của BPEL (xem Hình 3-2 minh họa một số ánh xạ thuộc loại này). Hình 3 1: Phân cấp khối cấu trúc của một tiến trình Hình 3 2: Ánh xạ của một số mẫu Trong [79], các tác giả đã phân tích những bất đồng cơ bản mức khái niệm (basic conceptual mismatches) giữa BPMN và BPEL. Theo phân tích, các bất đồng này là nguồn gốc gây ra các vấn đề khi chuyển đổi giữa hai ngôn ngữ. Đây là điều mà các kỹ thuật chuyển đổi cần lưu ý giải quyết. Có ba loại bất đồng đã được phát hiện: Bất đồng về khả năng biểu diễn lĩnh vực (Domain Representation Capability Mismatch); Bất đồng về khả năng hỗ trợ luồng điều khiển (Control Flow Support Mismatch); Bất đồng về cách thức biểu diễn tiến trình (Process Representation Paradigm Mismatch); Kỹ thuật ánh xạ được đề cập trong [74], ánh xạ các tiến trình được mô tả bằng Mô hình Tiến trình Tiêu chuẩn (Standard Process Models (SPM)) là các sơ đồ khái quát của các Ngôn ngữ Tiến trình Nghiệp vụ (Business Process Languages) như BPMN và UML (Unified Modeling Language). Mỗi SPM được xây dựng từ các phần tử (elements) và các luồng (transitions). Nó là một mô hình (model) có đúng một phần tử activity khởi tạo (initial activity) (là phần tử không có luồng vào) và đúng một phần tử activity kết thúc (final activity) (là phần tử không có luồng ra). Hướng tới sử dụng cấu trúc event handlers trong BPEL, kỹ thuật này có thể áp dụng cho bất kỳ loại SPM nào, chừng nào chúng không chứa các khóa sống (livelock). Để ánh xạ một tiến trình, kỹ thuật này bao gồm ba bước. Đầu tiên, các điều kiện tiên quyết (precondition sets) sẽ được tạo ra từ tất cả các phần tử activity của mô hình. Sau đó, các điều kiện này sẽ được chuyển thành tập các quy tắc Sự kiện-Điều kiện-Hành động (Event-Condition-Action (ECA) rules). Cuối cùng, các quy tắc này sẽ được dịch sang các cấu trúc event handler của BPEL. Mặc dù kỹ thuật này có ưu điểm là có thể được áp dụng cho nhiều loại sơ đồ BPMN, nhưng nó cũng tồn tại hai hạn chế cơ bản. Thứ nhất, do sử dụng cấu trúc event handler (là cơ chế tổng quát để xử lý các sự kiện và thường không có cấu trúc), nên code BPEL được tạo ra thường cũng không có cấu trúc, nghĩa là nó thường dài dòng và không dễ đọc. Thứ hai, code BPEL được tạo ra thường chứa nhiều cấu trúc activity rỗng. Để giải quyết các vấn đề trên, một cải tiến nhằm cố gắng phát hiện các khối activity có cấu trúc đã được đưa ra trong [74]. Sau đó các khối có cấu trúc này (được gọi là Clusterable Activity Block (CAB)), có thể được ánh xạ sang các phần tử activity có cấu trúc trong BPEL (xem Hình 3-3 (dựa theo hình ảnh trong [74])). Tuy nhiên, phương pháp cụ thể làm thế nào để tìm được các khối có cấu trúc lại không được trình bày trong nghiên cứu. Hình 3 3: Một sơ đồ tiến trình nghiệp vụ với các khối cấu trúc CAB Chính do thiếu sót trên, một vấn đề đã nảy sinh của kỹ thuật này được phát hiện bởi Blox [18]. Đó là số lượng khối cấu trúc CAB được tìm thấy có thể không cố định. Điều này có nghĩa là từ một tiến trình đầu vào lại có thể nhiều tiến trình đầu ra khác nhau: nó lại dẫn đến một vấn đề khá rắc rối là phải chọn ra tiến trình nào trong số đó. Trong nghiên cứu [3], các tác giả tiếp tục phát triển khái niệm khối cấu trúc CAB, nhưng đổi tên nó thành component hay pattern. Nói chung, không phải tất cả các loại sơ đồ tiến trình trong BPMN đều có thể được dịch sang BPEL. Do đó, nghiên cứu này chỉ tập trung vào việc dịch một loại sơ đồ tiến trình với tên gọi sơ đồ tiến trình lõi chính tắc (well-formed core business process diagram (WFC-BPD)). Có ba loại mẫu (pattern) đã được xác định và mỗi loại có một kỹ thuật ánh xạ riêng. Mẫu có cấu trúc đầy đủ (Well-structured patterns): là các mẫu mà có thể được ánh xạ đầy đủ sang một trong năm khối cấu trúc của BPEL (sequence, flow, pick, switch and while). Trong [3], có bảy mẫu của BPMN được xác định là có cấu trúc đầy đủ là: SEQUENCE, FLOW, PICK, SWITCH, REPEAT, WHILE, REPEAT+WHILE. Do ba mẫu lặp đều có thể được ánh xạ sang cấu trúc WHILE trong BPEL, nên ở đây chúng sẽ được gộp lại trong chỉ một mẫu WHILE. Do đó, ở đây chỉ còn năm mẫu (xem các từ Hình 3-4 đến 3-8) có thể được ánh xạ đầy đủ sang các cấu trúc của BPEL. Hình 3 4: Mẫu Sequence Hình 3 5: Mẫu Flow Hình 3 6: Mẫu Switch Hình 3 7: Mẫu Pick Hình 3 8: Mẫu While Mẫu có cấu trúc gần đủ (Quasi-structured patterns): là những mẫu mà có thể dễ dàng được chuyển đổi sang các mẫu có cấu trúc đầy đủ, để từ đó sẽ được ánh xạ sang các khối có cấu trúc trong BPEL. Mẫu bất chu trình dựa trên luồng (Flow based acyclic patterns): là loại mẫu tối thiểu không chứa chu trình và các gateway, trong đó thuộc một trong hai loại AND-fork hoặc AND-join. Các mẫu này có thể được ánh xạ sang các thành phần kết hợp của các khối có cấu trúc và các liên kết điều khiển (control links). Tư tưởng cơ bản của việc ánh xạ các mẫu loại này là việc rút gọn các cặp AND gateway nối với nhau. Có ba trường hợp kết nối được minh họa ở các Hình 3-9, 3-10 và 3-11. Hình 3 9: Rút gọn của hai “AND fork gateways” nối với nhau. Hình 3 10: Rút gọn của hai “AND join gateways” nối với nhau Hình 3 11: Rút gọn của hai AND gateways khác nhau nối với nhau (AND fork nối với AND join). Một cách tiếp cận khác trong việc dịch ngôn ngữ là dựa trên kỹ thuật chuyển đồ thị phụ thuộc sang tiến trình có cấu trúc như đã được giới thiệu trong [31] và sau đó được áp dụng để dịch từ BPMN sang BPEL bởi Blox [18]. Các hạn chế tồn tại Từ tổng quan về các kỹ thuật chuyển đổi từ ngôn ngữ hướng đồ thị sang ngôn ngữ có cấu trúc trình bày ở trên, có thể thấy rằng chúng vẫn còn tồn tại hai vấn đề sau: Thứ nhất: làm thế nào để phát hiện được các loại mẫu khác nhau trong tiến trình biểu diễn bằng ngôn ngữ nguồn (là ngôn ngữ hướng đồ thị như BPMN). Hầu hết các kỹ thuật chuyển đổi chỉ tập trung vào việc làm thế nào để chuyển đổi các mẫu từ tiến trình nguồn sang tiến trình đích, nhưng lại không hề đề cập đến vấn đề làm thế nào để phát hiện và tách được các mẫu ra khỏi tiến trình nguồn, để từ đó mới có thể chuyển đổi mẫu đó sang tiến trình đích. Theo nghiên cứu của luận án, vấn đề này cũng không hề đơn giản, đòi hỏi phải có những kỹ thuật phù hợp. Trong phần sau, luận án sẽ đề xuất giải thuật nhằm giải quyết một phần vấn đề này, đó là làm thế nào để phát hiện và tách ra được các mẫu có cấu trúc đầy đủ (well-structured patterns) đã được trình bày ở phần trên. Thứ hai: Tính đúng đắn của đa số các kỹ thuật chuyển đổi đã được đề xuất vẫn chưa được chứng minh đầy đủ. Tính đúng đắn của một kỹ thuật dịch, ở đây với nghĩa là ngữ nghĩa của tiến trình biểu diễn bằng ngôn ngữ đích phải giống với ngữ nghĩa của tiến trình biểu diễn bằng ngôn ngữ nguồn. Điều đó có nghĩa là một kỹ thuật dịch đúng sẽ bảo toàn ngữ nghĩa của tiến trình nguồn. Thiếu các chứng minh về tính đúng đắn sẽ làm giảm mức độ tin cậy và khả năng áp dụng các kỹ thuật này, vì chúng ta vẫn chưa chắc chắn là chúng có đúng không. Giải quyết vấn đề này nằm ngoài khuôn khổ của luận án. Đây cũng là hướng nghiên cứu mới có triển vọng. Giải thuật phát hiện mẫu có cấu trúc đầy đủ A. Một số khái niệm và tính chất cơ bản của đồ thị Định nghĩa 3 3: Một đồ thị G được gọi là đồ thị luồng điều khiển (control flow graph) nếu nó chứa hai nút phân biệt start và end sao cho mọi nút khác của G đều nằm trên một đường dẫn (path) nào đó từ nút start đến nút end. Nút start không có nút đứng trước (predecessors) và nút end không có nút đứng sau (successors). Tất cả các đồ thị mà chúng ta sẽ xét trong phần này đều là đồ thị luồng điều khiển, nên từ nay về sau tên này sẽ được gọi ngắn gọn là đồ thị. Định nghĩa 3 4: Cho một đồ thị G có chứa hai nút (hoặc hai cạnh) x và y. Ta nói rằng x chế ngự (dominate) y nếu mọi đường dẫn từ nút start đến y đều chứa x. Khi đó ta cũng nói x là phần tử chế ngự (dominator) của y. Ta nói rằng x chế ngự sau (post-dominate) y nếu mọi đường dẫn từ y đến nút end đều chứa x. Khi đó ta cũng nói x là phần tử chế ngự sau (post-dominator) của y. Ta nói rằng x là phần tử chế ngự liền kề (immediate dominator) của y nếu x chế ngự y và mọi phần tử chế ngự khác của y cũng sẽ chế ngự x. Ta nói rằng x là phần tử chế ngự sau liền kề (immediate post-dominator) của y nếu x chế ngự sau y và mọi phần tử chế ngự sau khác của y cũng sẽ chế ngự sau x. Theo quy ước, một nút không chế ngự chính nó, cũng không chế ngự sau chính nó. Định lý 3 1: [61] Ngoại trừ nút start, mỗi nút của đồ thị có đúng một nút chế ngự liền kề. Ngoại trừ nút end, mỗi nút của đồ thị có đúng một nút chế ngự sau liền kề. Định nghĩa 3 5: Hai cạnh (hay hai nút) u, v của đồ thị G được gọi là một cặp (couple), kí hiệu là couple(u, v), nếu u chế ngự v và v chế ngự sau u. Một couple(u, v) được gọi là một cặp liền kề (immediate couple) nếu u là phần tử chế ngự liền kề của v và v là phần tử chế ngự sau liền kề của u. Định lý 3 2: Hai cạnh u và v của một đồ thị G là một cặp couple(u, v) nếu và chỉ nếu tồn tại ít nhất một đường dẫn từ nút start đến nút end có chứa cả u và v, và mọi đường dẫn khác từ start đến end thì hoặc chứa cả u và v, hoặc không chứa cả u và v. Chứng minh: Nếu (u, v) là một cặp, thì u là phần tử chế ngự của v, và v là phần tử chế ngự sau của u. Theo định nghĩa về chế ngự và chế ngự sau ở trên, mọi đường dẫn từ start đến v đều chứa u, mọi đường dẫn từ u đến end đều chứa v. Do đó, mọi đường dẫn từ start đến end mà chứa u thì cũng chứa v và ngược lại. Và hiển nhiên phải tồn tại ít nhất một đường dẫn như vậy. Còn với mọi đường dẫn khác mà không có u, thì nó cũng không có v, bởi vì nếu không thì nó phải có u. Định nghĩa 3 6: Hai cạnh (hoặc nút) u và v của đồ thị G tạo thành biên của một vùng (a boundary of a region) nếu chúng là một cặp liền kề. u và v lần lượt được gọi là điểm vào (entry point) và điểm ra (exit point) của vùng. Định nghĩa 3 7: Cho đồ thị G. Một cạnh (hay một nút) e của G được gọi là nằm trong biên của một vùng (u, v) (hay nói ngắn gọn là nằm trong vùng) nếu: u là phần tử chế ngự của e và, v là phần tử chế ngự sau của e. Khi một cạnh nằm trong một vùng có nghĩa là cạnh đó nằm giữa điểm vào và điểm ra của vùng đó. Định nghĩa 3 8: Một tập các cạnh (hay các đỉnh) (e1, e2, ..., ek) của một đồ thị G tạo thành một vùng (region), ký hiệu reg(e1, e2, ..., ek), nếu (e1, ek) là biên của vùng và mọi cạnh (hay đỉnh) khác đều nằm trong biên của vùng. Trong các tiến trình BPMN, mỗi thành phần task hay event có đúng một cạnh vào (incoming edge) và một cạnh ra (outgoing edge). Do đó, mỗi cặp cạnh của một thành phần task hay event sẽ tạo thành một vùng và ta gọi nó là vùng tầm thường vì nó chỉ có biên mà không có cạnh nào khác nằm bên trong vùng. Định lý 3 3: Các mẫu trong số ba mẫu Flow, Pick và Switch đều tạo thành một vùng. Chứng minh: Ở đây chúng ta chỉ cần chứng mình cho mẫu Flow. Các chứng minh cho các mẫu khác hoàn toàn tương tự. Giả sử ta có mẫu Flow F(e1, e2, ..., ek) của đồ thị G. Theo định nghĩa của mẫu Flow, e1 là cạnh vào (incoming edge) duy nhất và ek là cạnh ra (outgoing edge) duy nhất của F. Hơn nữa, tồn tại ít nhất hai đường dẫn từ e1 đến ek, và mọi ei (2 £ i £ k-1) đều chỉ nằm trên một trong số các đường dẫn. Do đó, e1 là phần tử chế ngự liền kề của ek, và ek là phần tử chế ngự sau liền kề của e1, và mọi cạnh khác đều nằm giữa e1 và ek. Điều này cũng có nghĩa F là một vùng. □ Định lý 3 4: Mẫu Sequence là một dãy các vùng. Điều này có nghĩa là một mẫu Sequence S(e1, e2, ..., ek) có thể được tách ra thành p vùng tuần tự (sequential regions): r1(e1, e2, ..., ei1), r2(ei1, ..., ei2), ..., rp(ei(p-1), ..., ek), sao cho ∀ i=1..(p-1), cạnh ra của ri cũng là cạnh vào của ri+1. Chứng minh: Kết quả trên tương đối hiển nhiên, bởi vì mẫu Sequence bao gồm các task tuần tự (cũng là các vùng tầm thường) và các mẫu khác (chính là các vùng, theo Định lý 3-3). Định lý 3 5: [49] Nếu R1 và R2 là hai vùng của đồ thị G, chúng phải thỏa mãn một trong hai điều kiện sau: Hai tập các nút trong R1 và R2 là không giao nhau, hoặc R1 nằm trong R2 (nghĩa là tất cả các cạnh của R1 đều nằm trong R2) hoặc ngược lại. Từ Định lý 3-5 có thể dễ dàng suy ra hai hệ quả sau: Hệ quả 1: Tất cả các vùng của một đồ thị có thể được tổ chức thành một cây. Hệ quả 2: Vùng R1(e1, e2, ..., ek) nằm trong vùng R2 nếu e1 và ek nằm trong R2, hoặc R1 nằm trong vùng R3 khác, mà R3 lại nằm trong vùng R2. Định nghĩa 3 9: Một danh sách các vùng R1, R2,..., Rk được gọi là khả tuần tự (sequenceable) nếu chúng
File đính kèm:
 luan_an_khung_cong_tac_da_dung_trong_moi_truong_tinh_toan_lu.docx
luan_an_khung_cong_tac_da_dung_trong_moi_truong_tinh_toan_lu.docx INFORMATION ON NEW CONCLUSIONS OF DOCTORAL THESIS.docx
INFORMATION ON NEW CONCLUSIONS OF DOCTORAL THESIS.docx INFORMATION ON NEW CONCLUSIONS OF DOCTORAL THESIS.pdf
INFORMATION ON NEW CONCLUSIONS OF DOCTORAL THESIS.pdf LuanAn-Binh-Final.pdf
LuanAn-Binh-Final.pdf THÔNG TIN TÓM TẮT VỀ NHỮNG KẾT LUẬN MỚI CỦA LUẬN ÁN.docx
THÔNG TIN TÓM TẮT VỀ NHỮNG KẾT LUẬN MỚI CỦA LUẬN ÁN.docx THÔNG TIN TÓM TẮT VỀ NHỮNG KẾT LUẬN MỚI CỦA LUẬN ÁN.pdf
THÔNG TIN TÓM TẮT VỀ NHỮNG KẾT LUẬN MỚI CỦA LUẬN ÁN.pdf TomTatLuanAn-A4-V3.docx
TomTatLuanAn-A4-V3.docx TomTatLuanAn-A4-V3.pdf
TomTatLuanAn-A4-V3.pdf TRÍCH YẾU LUẬN ÁN.docx
TRÍCH YẾU LUẬN ÁN.docx TRÍCH YẾU LUẬN ÁN.pdf
TRÍCH YẾU LUẬN ÁN.pdf

