Luận án Một số thuật toán tuần tự và song song trên mạng đồ thị truyền thống

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
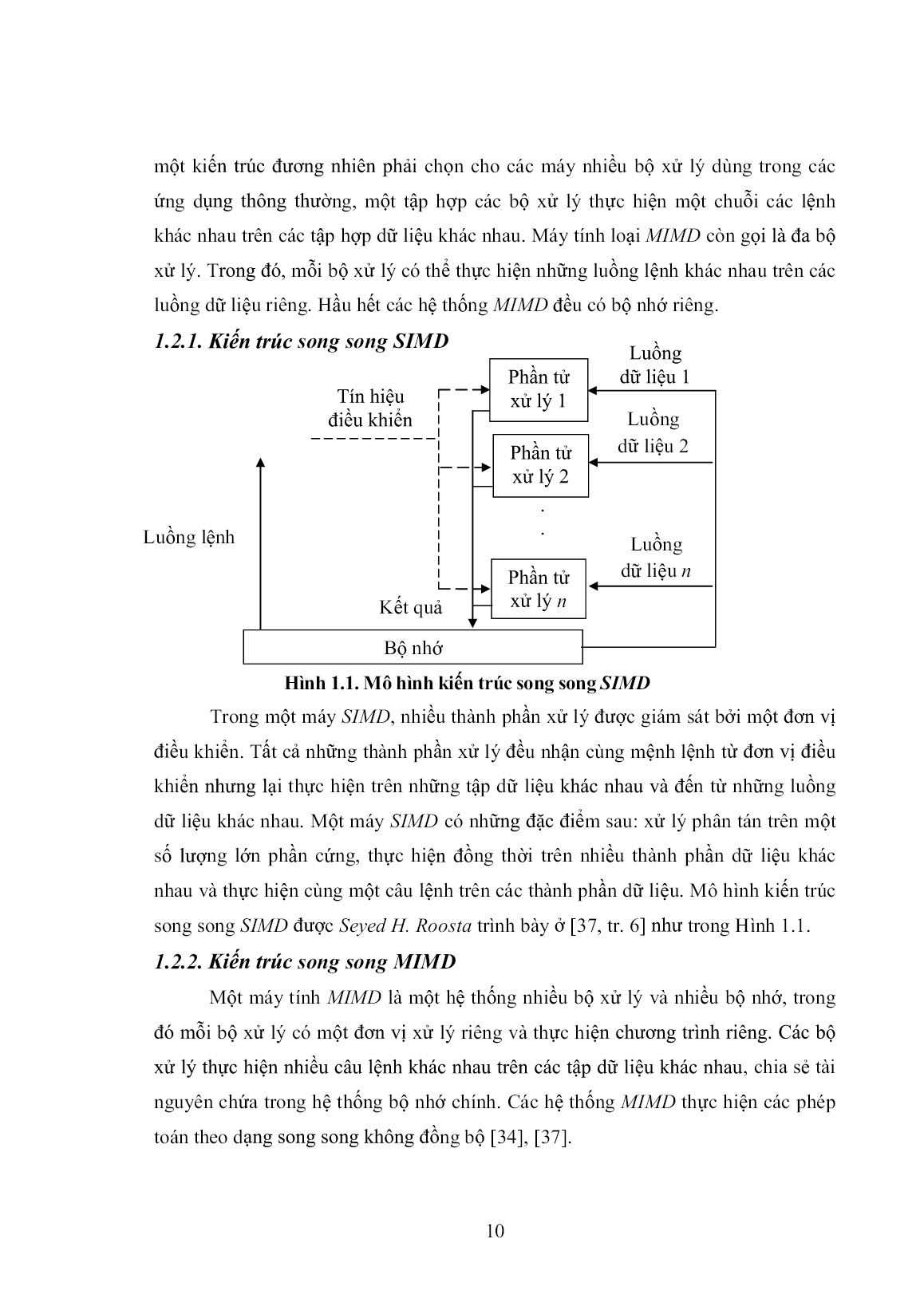
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Luận án Một số thuật toán tuần tự và song song trên mạng đồ thị truyền thống", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Luận án Một số thuật toán tuần tự và song song trên mạng đồ thị truyền thống

ây dưṇ g luồng trước xuất phát f với các cung đi từ đỉnh nguồn có luồng
bằng khả năng thông qua , còn các cung khác có luồng bằng 0. Chọn hàm độ
cao h nào đó trong maṇ g G.
- Bổ sung vào f luồng sau xuất phát với các cung đi đ ến đỉnh đích (trừ cung
đã có luồng trước dương) có luồng bằng khả năng thông qua . Chọn hàm độ
sâu d nào đó trong mạng G.
Bước 2. Tiêu chuẩn dừ ng:
Nếu không có đỉnh lêc̣ h thì dừ ng, luồng f trên mạng trở thành luồng cưc̣ đaị.
Bước 3. Xử lý đỉnh lêc̣ h:
46
- Chọn đỉnh lệch u có độ lệch dương.
Nếu tồn taị cung ưu tiên (u, v) Ef thì đẩy trên cung (u, v) môṭ luồng có giá tri ̣
min{delta, cf(u, v)}, trong đó delta là đô ̣lêc̣ h luồng của đỉnh u.
Nếu không tồn taị cung ưu tiên đi từ u, thì tăng độ cao của đỉnh u như sau:
h(u)= 1 + min{h(v) | (u, v) Ef}.
- Chọn đỉnh lệch v có độ lệch âm.
Nếu tồn taị cung ưu tiên (u, v) Ef thì kéo trên cung (u, v) môṭ luồng có giá tri ̣
min{ delta, cf(u, v)}, trong đó delta (< 0) là độ lệch luồng của đỉnh v. Nếu
không tồn taị cung ưu tiên đi đến v, thì tăng độ sâu của đỉnh v như sau:
d(v)= 1 + min{d(u) | (u, v) Ef}. Quay laị bướ c 2.
Từ các tính chất của thuật toán đẩy luồng trước và thuật toán kéo luồng sau
ta suy ra các mệnh đề và định lý sau:
Mêṇ h đê ̀ 2.7. Phương pháp hỗn hợp đẩy kéo luồng luôn bảo toàn tính chất của
hàm độ cao h và hàm độ sâu d.
2.4.2.2. Thuâṭ toá n hỗn hợp đẩy kéo luồng
Đây là thuâṭ toán cu ̣thể thuôc̣ phương pháp h ỗn hợp đẩy kéo luồng. Ở đây
các đỉnh lệch dương được đẩy vào hàng đợi Q+ và các đỉnh lêc̣ h âm đươc̣ đẩy vào
hàng đợi Q .
Với mỗi đỉnh lêc̣ h dương lấy từ hàng đơị Q+, ta se ̃ đẩy luồng vào các cung ưu
tiên môṭ cách tối đa cho tới khi đỉnh trở thành không lêc̣ h hoăc̣ không còn cung ưu
tiên nữa. Nếu không còn cung ưu tiên nữa và đỉnh còn lêc̣ h thì ta tăng đô ̣ cao và đẩy
nó vào hàng đợi Q+.
Với mỗi đỉnh lêc̣ h âm lấy từ hàng đơị Q , ta se ̃ kéo luồng vào các cung ưu
tiên môṭ cách tối đa cho tới khi đỉnh trở thành không lêc̣ h hoăc̣ không còn cung ưu
tiên nữa. Nếu không còn cung ưu tiên nữa và đỉnh còn lêc̣ h thì ta tăng đô ̣sâu và đẩy
nó vào hàng đợi Q . Bây giờ ta mô tả thuâṭ toán hỗn hợp đẩy kéo luồng như sau:
Bước 1. Khởi taọ :
- Xây dưṇ g luồng trước xuất phát f với các cung đi từ đỉnh nguồn có luồng
bằng khả năng thông qua, còn các cung khác có luồng bằng 0.
47
- Chọn hàm độ cao h(v) là độ dài đường đi ngắn nhất từ v đến đỉnh đích z.
- Đẩy các đỉnh lệch dương vào hàng đợi Q+.
- Bổ sung vào f luồng sau xuất phát với các cung đi đ ến đỉnh đích (trừ cung
đã có luồng trước dương) có luồng bằng khả năng thông qua.
- Chọn hàm độ sâu d(v) là độ dài đường đi ngắn nhất từ đỉnh a đến đỉnh v.
- Đẩy các đỉnh lệch âm vào hàng đợi Q .
Bước 2. Tiêu chuẩn dừ ng:
- Nếu Q+ = ∅ và Q =∅, luồng f trở thành luồng cưc̣ đaị, kết thúc.
- Ngược lại sang bướ c 3.
Bước 3. Xử lý đỉnh lêc̣ h:
- Lấy đỉnh lêc̣ h u từ hàng đơị Q+.
Duyêṭ các cung ưu tiên (u, v) Ef . Đẩy trên cung (u, v) môṭ luồng có giá tri ̣
min{delta, cf(u, v)}, trong đó delta là độ lệch luồng của đỉnh u.
Nếu đỉnh v là đỉnh lệch mới, thì đẩy đỉnh v vào hàng đợi Q+.
Nếu đỉnh u vâñ còn lêc̣ h, thì tăng độ cao của đỉnh u như sau:
h(u)= 1 + min{h(v) | (u, v) Ef}. Đẩy u vào hàng đợi Q+.
- Lấy đỉnh lêc̣ h v từ hàng đơị Q .
Duyêṭ các cung ưu tiên (u, v) Ef. Kéo trên cung (u, v) môṭ luồng có giá tri ̣
min{ delta, cf(u, v)}, trong đó delta (< 0) là độ lệch luồng của đỉnh v. Nếu
đỉnh u là đỉnh lệch mới, thì đẩy đỉnh u vào hàng đợi Q . Nếu đỉnh v vâñ còn
lêc̣ h, thì tăng độ sâu của đỉnh v như sau: d(v)= 1 + min{d(u) | (u, v) Ef} sau
đó đẩy v vào hàng đợi Q . Quay laị bướ c 2.
Mêṇ h đê ̀ 2.8. Trong quá trình thưc̣ hiêṇ thuật toán hỗn hợp đẩy kéo luồng, luôn
tồn taị đường đi điṇ h hướng từ mỗi đỉnh lêc̣ h dương đến đỉnh nguồn và luôn tồn taị
đường đi điṇ h hướng t ừ đỉnh đích đ ến mỗi đỉnh lêc̣ h âm trong maṇ g thăṇ g dư , và
không tồn taị đường đi điṇ h hướng từ đỉnh nguồn đến đích trong maṇ g thăṇ g dư.
Hê ̣quả 2.5. Trong quá trình thưc̣ hiêṇ thuật toán hỗn hợp đẩy kéo luồng, đô ̣cao
và độ sâu mỗi đỉnh luôn nhỏ hơn 2.|V|.
48
Điṇ h lý 2.4. Thuật toán hỗn hợp đẩy kéo luồng tìm luồng cực đại là đúng.
Tương tự như thuật toán đẩy luồng trước và thuật toán kéo luồng sau, ta có
2
độ phức tạp của phương pháp hỗn hợp đẩy kéo luồng là O(|V| |E|).
2.4.2.3. Ví dụ minh họa
Tìm luồng cực đại f bằng thuật toán hỗn hợp đẩy kéo luồng của mạng đồ thị
như trong Hình 2.23. Thứ tự các đỉnh là a, b, c, d, e, f, g, h, i, z. Kết quả cân bằng
các đỉnh được biểu diễn trên các Hình 2.24 đến Hình 2.32.
c
b f h
2 2 2
3 3
a 2 2 z
3
5 3 2
2
d e g i
Hình 2.23. Mạng đồ thị G
c(3, 0, 2) f(2, 0, 3)
b(4, 3, 1) h(1, -3, 4)
2, 0 2, 0 2, 0
3, 3 3, 3
2, 0 2, 0
a(5, -8, 0) z(0, 6, 5)
3, 3
5, 5 3, 0 2, 0
g(2, 0, 3) 2, 0 i(1, -3, 4)
d(4, 5, 1) e(3, 0, 2)
Hàng đợi Q+ :b|d Hàng đợi Q-:h|i
Hình 2.24. Mạng đồ thị khởi tạo
o Cân bằng b Q+. Cân bằng đỉnh h Q-
b(6, 1, 1) c(3, 2, 2) f(2, -2, 3) h(1, 0, 4)
2, 0
2, 2 2, 2 3, 3
3, 3
2, 1
a(5, -8, 0) 2, 0
3, 3 z(0, 6, 5)
5, 5 3, 0 2, 0
e(3, 0, 2) g(2, -1, 3) 2, 0 i(1, -3, 4)
d(4, 5, 1)
Hàng đợi Q : b|d|c|b Hàng đợi Q-:h|i|f|g
+
Hình 2.25. Mạng đồ thị cân bằng b, h
o Cân bằng d Q+. Cân bằng đỉnh i Q-.
49
b(6, 1, 1) c(3, 4, 2) f(2, -2, 3) h(1, 0, 4)
o 2, 2 2, 0 2, 2
3, 3 3, 3
a(5, -8, 0) 2, 2 2, 1 z(0, 6, 5)
3, 3
5, 5 3, 3 2, 0
g(2, -3, 3) 2, 2 i(1, -1, 6)
d (4, 0, 1) e(3, 3, 2)
Hàng đợi Q : b|d|c|b|e Hàng đợi Q-:h|i|f|g|i
+
Hình 2.26. Mạng đồ thị cân bằng d, i
o Cân bằng c Q+. Cân bằng đỉnh f Q-
b(6, 1, 1) c(5, 2, 2) f(2, 0, 3) h(1, 0, 4)
2, 2 2, 2 2, 2
3, 3 3, 3
a(5, -8, 0) 2, 2 2, 1 z(0, 6, 5)
3, 3
5, 5 3, 3 2, 0
d(4, 0, 1) e(3, 3, 2) g(2, -3, 3) 2, 2 i(1, -1, 6)
Hàng đợi Q+ : b|d|c|b|e|c Hàng đợi Q-:h|i|f|g|i|
Hình 2.27. Mạng đồ thị cân bằng c, f
o Cân bằng b Q+. Cân bằng đỉnh g Q-
b(6, 0, 1) c(5, 2, 2) f(2, 0, 3) h(1, 0, 4)
2, 2 2, 2 2, 2
3, 2
3, 3
z(0, 6, 5)
a(5, -7, 0) 2, 2 2, 1
3, 3
5, 5 3, 3 2, 2
2, 2 i(1, -1, 6)
d(4, 0, 1) e(3, 1, 2) g(2, -1, 5)
Hàng đợi Q-:h|i|f|g|i|g
Hàng đợi Q+ : b|d|c|b|e|c
Hình 2.28. Mạng đồ thị cân bằng b, g
o Cân bằng e Q+, tăng h(e). Cân bằng đỉnh i Q-
b(6, 0, 1) c(5, 2, 2) f(2, 0, 4) h(1, 0, 4)
2, 2 2, 2 2, 2
3, 2 3, 3
z(0, 5, 5)
a(5, -7, 0) 2, 2 2, 1
3, 2
5, 5 3, 3 2, 2
d(4, 0, 1) e(5, 1, 2) g(2, -1, 5) 2, 2 i(1, 0, 6)
Hàng đợi Q : b|d|c|b|e|c|e Hàng đợi Q-:h|i|f|g|i|g
+
Hình 2.29. Mạng đồ thị cân bằng e, i
50
o Cân bằng c Q+. Cân bằng g Q-
b(6, 0, 1) c(5, 0, 2) f(2, 0, 4) h(1, -1, 4)
2, 2 2, 2 2, 2 3, 3
3, 2
a(5, -7, 0) 2, 0 2, 0 z(0, 5, 5)
3, 2
5, 5 3, 3 2, 2
2, 2
d(4, 2, 1) e(5, 1, 2) g(2, 0, 5) i(1, 0, 6)
Hàng đợi Q+ : b|d|c|b|e|c|e|d Hàng đợi Q-:h|i|f|g|i|f|g|h
Hình 2.30. Mạng đồ thị cân bằng c, g
o Cân bằng e Q+. Cân bằng h Q-. Tăng d(h)=1+5=6
b(6, 0, 1) c(5, 0, 2) f(2, 0, 4) h(1, -1, 6)
2, 2 2, 2 2, 2
3, 3
3, 2 z(0, 5, 5)
2, 0 2,0
a(5, -4, 0) 3, 2
5, 5 3, 2 2, 2 2, 2
d(4, 3, 1) e(5, 0, 2) g(2, 0, 5) i(1, 0, 6)
Hàng đợi Q :h|i|f|g|i|f|g|h|h
Hàng đợi Q+ : b|d|c|b|e|c|e|d -
Hình 2.31. Mạng đồ thị cân bằng e, h
o Cân bằng d Q+. tăng h(d)=1+5=6 và cân bằng tiếp d Q+ và h Q-.
b(6, 0, 1) c(5, 0, 2) f(2, 0, 4) h(1, 0, 6)
2, 2 2, 2 2, 2
3, 2
3, 2
a(5, -4, 0) 2, 0 2, 0 z(0, 4, 5)
3, 2
5, 2 3, 2 2, 2 2, 2
d(6, 0, 1) e(5, 0, 2) g(2, 0, 5) i(1, 0, 6)
Hàng đợi Q+ : b|d|c|b|e|c|e|d|d Hàng đợi Q-:h|i|f|g|i|f|g|h|h
Hình 2.32. Mạng đồ thị cân bằng d, h
Q+ ,Q- đều rỗng. Kết luận luồng cực đại cần tìm là 4.
2.4.3. Thuật toán song song hỗn hợp đẩy kéo luồng tìm luồng cực đại
2.4.3.1. Giới thiệu
51
Thuật toán đẩy luồng trước và thuật toán kéo luồng sau bắt đầu thực hiện ở
đỉnh nguồn và đỉnh đích. Vì vậy, nếu ta thực hiện song song thì việc thiết kế thuật
toán rất dễ dàng, độ phức tạp giảm so với thuật toán đẩy luồng trước là đáng kể.
Thuật toán đẩy luồng trước, kéo luồng sau và thuật toán hỗn hợp đẩy kéo
luồng đều có độ phức tạp là O(|V|2|E|). Để giảm độ phức tạp thời gian tính toán,
chúng tôi đề xuất thu ật toán song song hỗn hợp đẩy kéo luồng tìm luồng cực đại.
2.4.3.2. Ý tưởng của thuật toán song song
Thuật toán song song sẽ dùng ba bộ xử lý, một bộ xử lý P0 quản lý dữ liệu,
gửi và nhận dữ liệu từ hai bộ xử lý phụ P1, P2. Trong hai bộ xử lý phụ, một bộ xử lý
P1 sẽ đẩy luồng từ Q+ và bộ xử lý P2 sẽ kéo luồng từ Q-. Các bộ xử lý phụ kết thúc
khi các Q+ và Q- là rỗng.
2.4.3.3. Xây dựng thuật toán song song
Đầu vào: Đồ thị G(V, E, c) với nguồn a, đích z, khả năng thông qua:
c= {ci, j | (i, j) E} (28)
Ba bộ xử lý P0, P1 và P2. Trong đó, P0 là bộ xử lý chính, P1 và P2 là hai bộ
xử lý phụ.
Đầu ra: Luồng cực đại:
f = {fi, j | (i, j) E} (29)
Các bước:
Bước 1: Bộ xử lý chính thực hiện.
- Bộ xử lý chính khởi tạo: h, d, e, f, c, Q+, Q-.
Bước 2: Bộ xử lý chính kiểm tra kết thúc.
- Nhận dữ liệu từ các bộ xử lý phụ (nếu các bộ xử lý phụ có gửi dữ liệu đến)
- Bộ xử lý chính kiểm tra nếu Q+, Q- là rỗng và các bộ xử lý P1 và P2 kết
thúc, thì luồng f trở thành luồng cưc̣ đaị, kết thúc.
Ngược lại sang bướ c 3.
Bước 3: Bộ xử lý chính thực hiện kiểm tra.
- Bộ xử lý chính lấy đỉnh u từ Q+ và y từ Q-.
- Gửi h, e, f, u, Q+ đến bộ xử lý P1. Gửi d, e, f, đỉnh y, Q- đến bộ xử lý P2
52
- Bộ xử lý chính kiểm tra: Nếu với mọi cung ưu tiên (u, v) Ef và với mọi
cung ưu tiên (x, y) Ef mà u trùng với x hoặc y trùng với v thì sang bước 5.
Ngược lại sang bước 4.
Bước 4: Bộ xử lý phụ P1 và P2 thực hiện song song các công việc sau đây:
- Hai bộ xử lý phụ nhận dữ liệu mà bộ xử lý chính P0 gửi đến.
- Bộ xử lý P1 thực hiện.
Đẩy luồng trước: lấy đỉnh lệch u từ hàng đơị Q+. Duyêṭ các cung ưu tiên
(u, v) Ef . Đẩy trên cung (u, v) môṭ luồng có giá tri ̣min{delta, cf(u, v)}, trong
đó delta là độ lệch luồng của đỉnh u. Nếu đỉnh v là đỉnh lệch mới, thì đẩy
đỉnh v vào hàng đợi Q+.
Nếu đỉnh u vâñ còn lêc̣ h, thì tăng độ cao của đỉnh u như sau:
h(u)= 1 + min{h(v) | (u, v) Ef}. Sau đó, đẩy u vào hàng đợi Q+.
Chuyển Q+, h, e, f, cf về bộ xử lý chính.
- Bộ xử lý P2 thực hiện.
Kéo luồng sau: lấy đỉnh lệch y từ Q-. Duyêṭ các cung ưu tiên (x, y) Ef . Kéo
trên cung (x, y) môṭ luồng có giá tri ̣min{ delta, cf(x, y)}, trong đó delta (< 0)
là độ lệch luồng của đỉnh y. Nếu đỉnh x là đỉnh lệch mới, thì đẩy đỉnh x vào
hàng đợi Q-.
Nếu đỉnh y vâñ còn lêc̣ h, thì tăng độ sâu của đỉnh y như sau:
d(y)= 1 + min{d(x) | (x, y) Ef}. Sau đó, đẩy y vào hàng đợi Q .
Chuyển Q-, d, e, f về bộ xử lý chính.
Quay lại bước 2.
Bước 5: Hai bộ xử lý P1 và P2 thực hiện tuần tự.
- Bộ xử lý phụ P1 thực hiện
Nhận dữ liệu từ P0 gửi đến ở bước 3.
Đẩy luồng trước: lấy đỉnh lệch u từ Q+. Duyêṭ các cung ưu tiên (u, v) Ef.
Đẩy trên cung (u, v) môṭ luồng có giá tri ̣min{delta, cf(u, v)}, (delta là độ lệch
luồng của đỉnh u). Nếu đỉnh v là đỉnh lệch mới, thì đẩy v vào Q+.
Nếu đỉnh u vâñ còn lêc̣ h, thì tăng độ cao của đỉnh u như sau:
53
h(u)= 1 + min{h(v) | (u, v) Ef}. Sau đó, đẩy u vào hàng đợi Q+.
Chuyển Q+, h, e, f, về bộ xử lý chính. Chuyển e, f đến bộ xử lý P2.
- Bộ xử lý phụ P2 thực hiện.
Nhận dữ liệu từ P0 gửi đến ở bước 3 và nhận dữ liệu P1 gửi đến ở bước 5.
Kéo luồng sau:
Lấy đỉnh lệch y từ hàng đơị Q-. Duyêṭ các cung ưu tiên (x, y) Ef . Kéo trên
cung (x, y) môṭ luồng có giá tri ̣min{ delta, cf(x, y)}, trong đó delta (< 0) là
đô ̣lêc̣ h luồng của đỉnh y.
Nếu đỉnh x là đỉnh lệch mới, thì đẩy đỉnh x vào hàng đợi Q-.
Nếu đỉnh y vâñ còn lêc̣ h, thì tăng độ sâu của đỉnh y như sau:
d(y)= 1 + min{d(x) | (x, y) Ef}. Sau đó, đẩy y vào hàng đợi Q .
Chuyển Q-, d, e, f, về bộ xử lý chính.
Quay lại bước 2
Điṇ h lý 2.5. Thuật toán song song hỗn hợp đẩy kéo luồng tìm luồng cực đại là
đúng.
Chứng minh: Ta xét hai trường hợp sau:
- Trường hợp 1: P1 và P2 thực hiện đồng thời, nghĩa là việc cân bằng các
đỉnh ở Q+ và các đỉnh ở Q- là độc lập nhau. Trong trường hợp này sẽ lấy u từ Q+ và
y từ Q- thỏa với mọi cung ưu tiên (u, v) Ef và với mọi cung ưu tiên (x, y) Ef mà u
không trùng với x và y không trùng với v để P1 và P2 cân bằng. Sau mỗi lần cân
bằng thì bộ xử lý P0 sẽ đồng bộ hóa dữ liệu của các đỉnh. Vậy từ thuật toán tuần tự
suy ra việc thực hiện song song trong trường hợp này là đúng.
- Trường hợp 2: P1 và P2 thực hiện tuần tự, nghĩa là việc cân bằng các đỉnh ở
Q+ và các đỉnh ở Q- là tuần tự, trong đó P1 thực hiện xong rồi gửi kết quả đến P2 và
P2 tiếp tục thực hiện. Trong trường hợp này sẽ lấy u từ Q+ và y từ Q- thỏa với mọi
cung ưu tiên (u, v) Ef và với mọi cung ưu tiên (x, y) Ef mà u trùng với x hoặc y
trùng với v để P1 và P2 cân bằng. Suy ra, việc kéo đẩy luồng trong trường hợp này
là đúng vì phù hợp với thuật toán tuần tự.
2.4.3.4. Ví dụ minh họa
54
Tìm luồng cực đại f trên ba bộ xử lý P0, P1, P2 của đồ thị được trình bày như
trong Hình 2.23.
Pha 1:
Bước 1: Khởi tạo h, d, e, f, c, Q+, Q- như trong thuật toán tuần tự.
Bước 2: Bộ xử lý chính kiểm tra Q+={b, d}, Q-={h, i} khác rỗng nên sang bước 3.
Bước 3: Bộ xử lý chính lấy b từ Q+ và h từ Q-. Sau đó, kiểm tra không có cung ưu
tiên (b, v) Ef và cung ưu tiên (x, h) Ef mà b trùng với x hoặc h trùng với v
nên sang bước 4.
Bước 4: P1 và P2 thực hiện song song, tức là ở P1 cân bằng đỉnh b thuộc Q+ và P2 sẽ
cân bằng đỉnh h tại Q- và có kết quả ở Hình 2.33. Các bộ xử lý phụ chuyển kết
quả về bộ xử lý chính.
Quay lại bước 2
Pha 2:
Bước 2: Bộ xử lý chính kiểm tra Q+={d, c, b}, Q-={i, f, g} khác rỗng sang bước 3.
Bước 3: Bộ xử lý chính lấy d từ Q+ và i từ Q-. Sau đó, kiểm tra không có cung ưu
tiên (d, v) Ef và cung ưu tiên (x, i) Ef mà d trùng với x hoặc i trùng với v
nên sang bước 4.
Bước 4: P1 và P2 thực hiện song song, tức là ở P1 cân bằng đỉnh d thuộc Q+ và P2
cân bằng đỉnh i tại Q- và có kết quả ở Hình 2.34. Các bộ xử lý phụ chuyển
kết quả về bộ xử lý chính.
Quay lại bước 2.
f(2, -2, 3)
b(6, 1, 1) c(3, 2, 2) h(1, 0, 4)
2, 0
2, 2 2, 2 3, 3
3, 3
2, 1
a(5, -8, 0) 2, 0 z(0, 6, 5)
3, 3
5, 5 3, 0 2, 0 2, 0
d(4, 5, 1) e(3, 0, 2) g(2, -1, 3) i(1, -3, 4)
Hàng đợi Q : b|d|c|b Hàng đợi Q :h|i|f|g
+ -
Hình 2.33. Mạng đồ thị cân bằng b ở bộ xử lý P1, và cân bằng h ở bộ xử lý P2
55
b(6, 1, 1) c(3, 4, 2) f(2, -2, 3) h(1, 0, 4)
2, 0
2, 2 2, 2 3, 3
3, 3
a(5, -8, 0) 2, 2 2, 1 z(0, 6, 5)
5, 5 3, 3 2, 0 2, 2 3, 3
g(2, -3, 3) i(1, -1, 6)
d(4, 0, 1) e(3, 3, 2)
Hàng đợi Q+ : b|d|c|b|e Hàng đợi Q-:h|i|f|g|i
Hình 2.34. Mạng đồ thị cân bằng d ở bộ xử lý P1 và cân bằng i ở bộ xử lý P2
Pha 3:
Bước 2: Bộ xử lý chính kiểm tra Q+={c, b, e}, Q-={f, g, i} khác rỗng sang bước 3.
Bước 3: Bộ xử lý chính lấy c từ Q+ và f từ Q-. Sau đó kiểm tra có đẩy cung ưu tiên
(c, f) Ef và kéo cung ưu tiên (c, f) Ef, 2 cung này trùng nhau qua bước 5.
Bước 5: P1, P2 thực hiện tuần tự, tức là P1 cân bằng đỉnh c thuộc Q+ trước rồi gửi
kết quả đến P2 và P2 sẽ cân bằng đỉnh f tại Q- và có kết quả ở Hình 2.35. Các
bộ xử lý phụ P2 chuyển kết quả về bộ xử lý chính, sau đó quay lại bước 2.
b(6, 1, 1) c(5, 2, 2) f(2, 0, 3) h(1, 0, 4)
2, 2 2, 2 2, 2
3, 3 3, 3
a(5, -8, 0) 2, 2 2, 1 z(0, 6, 5)
3, 3
5, 5 3, 3 2, 0 2, 2
d(4, 0, 1) e(3, 3, 2) g(2, -3, 3) i(1, -1, 6)
Hàng đợi Q+ : b|d|c|b|e|c Hàng đợi Q-:h|i|f|g|i
Hình 2.35. Mạng đồ thị cân bằng c ở bộ xử lý P1, và cân bằng f ở bộ xử lý P2
Tương tự như vậy thuật toán kết thúc sau khi thực hiện xong pha 9.
Pha 4: P1, P2 thực hiện đồng thời. P1 cần bằng đỉnh b thuộc Q+, P2 sẽ cân bằng đỉnh
g tại Q-
Pha 5: P1, P2 thực hiện đồng thời. P1 cần bằng đỉnh e thuộc Q+, P2 sẽ cân bằng đỉnh
i tại Q-.
Pha 6: P1, P2 thực hiện đồng thời. P1 cần bằng đỉnh c thuộc Q+, P2 sẽ cân bằng đỉnh
g tại Q-.
Pha 7: P1, P2 thực hiện đồng thời. P1 cần bằng đỉnh e thuộc Q+, P2 sẽ cân bằng đỉnh
56
h tại Q-.
Pha 8: P1, P2 thực hiện đồng thời. P1 cần bằng đỉnh d thuộc Q+, P2 sẽ cân bằng đỉnh
h tại Q-. Q- =∅.
Pha 9: P1 cần bằng đỉnh d thuộc Q+. Q+ =∅. Kết thúc.Suy ra luồng cực đại f=4.
2.4.3.5. Kết quả thực nghiệm
a. Dữ liệu thực nghiệm
Dữ liệu thực nghiệm được tạo ngẫu nhiên có cấu trúc giống như trong thuật
toán song song đẩy luồng trước được trình bày mục 2.3.2.6.
b. Môi trường thực nghiệm.
Chúng tôi thực nghiệm trên hệ thống đa bộ xử lý với cấu trúc gồm một bộ xử
lý chính được gọi Server và các bộ xử lý phụ được gọi là Client. Các bộ xử lý có
cấu hình gần tương đương nhau là cấu hình Intel Core Dual T2450, bộ nhớ 1G.
Thuật toán được cài đặt bằng ngôn ngữ Java hệ điều hành Win 7 với hệ quản trị cơ
sơ MySQL.
Hình 2.36. Giao diện Client
57
Hình 2.37. Giao diện Server
c. Kết quả thực nghiệm
Kết quả thực nghiệm để kiểm tra tính đúng đắn của mạng đồ thị như trong
Hình 2.23 được biểu diễn bằng giao diện như trong Hình 2.36 và Hình 2.37. Chúng
tôi tạo ngẫu nhiên mạng đồ thị gồm 5500 và 7500 với độ giãn nở khác nhau và cho
thử nghiệm thực toán tuần tự và song song trên 2 bộ xử lý thì kết quả thực hiện song
song có thời gian giảm so với thuật toán tuần tự, cụ thể là mức độ tăng tốc
(Speedup) của thuật toán song song so với thuật toán tuần tự đối với mạng đồ thị
5500 đỉnh và 7500 đỉnh tương ứng là 1.62 và 1.79.
58
d. Nhận xét
Thuật toán song song làm giảm thời gian đáng kể so với thuật toán tuần tự
được thể hiện qua mức độ tăng tốc của 2 mạng đồ thị nêu trên. Việc tính toán của
thuật toán đẩy luồng trước và kéo luồng sau là độc lập nhau nên việc xử lý song
song chỉ làm chậm thời gian khi các bộ xử lý thực hiện đồng thời. Vì vậy, mức độ
tăng tốc càng lớn (thời gian càng giảm) khi dữ liệu đầu vào là lớn. Tuy nhiên, mức
độ tăng tốc cũng phụ thuộc vào độ giãn nở của đồ thị.
2.4.3.6. Kết luận
Từ thuật toán đẩy luồng trước và thuật toán kéo luồng sau, chúng tôi đã đề
xuất thuật toán mới: thuật toán hỗn hợp đẩy kéo luồng tìm luồng cực đại. Hơn nữa,
để giảm thời gian tính toán thì thuật toán song song tìm luồng cực đại dựa trên thuật
toán hỗn hợp được đề xuất. Chúng tôi chứng minh chi tiết các định lý, mệnh đề liên
quan đến thuật toán và phần thực nghiệm cho kết quả chính xác và thuật toán song
song giảm thời gian so với thuật toán tuần tự.
2.5. Kết luận chƣơng
Trong chương hai, chúng tôi đã trình bày chi tiết thuật toán tuần tự đẩy luồng
trước được kế thừa từ các nghiên cứu đã có và đề xuất thuật toán hỗn hợp đẩy kéo
luồng tìm luồng cực đại. Từ đó, chúng tôi tối ưu thuật toán song song đẩy luồng
trước và đề xuất thuật toán song song hỗn hợp đẩy kéo luồng tìm luồng cực đại. Các
thuật toán song song được đề xuất cụ thể, rõ ràng. Các định lý, mệnh đề và hệ quả
liên quan đến các thuật toán đều được chứng minh rõ ràng. Các thuật toán song
song đều phân tích thời gian tính toán. Đặc biệt, nội dung chính của chương này
được chúng tôi công bố trong 3 bài báo chuyên ngành Công nghệ Thông tin và
được liệt kê ở tài liệu [1], [3], [4] trong danh mục các công trình của tác giả.
59
CHƢƠNG 3. MỘT SỐ THUẬT TOÁN SONG SONG TÌM
ĐƢỜNG ĐI NGẮN NHẤT VÀ TÌM LUỒNG CỰC ĐẠI TRÊN
MẠNG ĐỒ THỊ MỞ RỘNG
Các thuật toán tuần tự tìm đường đi ngắn nhất trên đồ thị mở rộng đã được
nghiên cứu trong [9], [22], [27] và thuật toán tuần tự tìm luồng cực đại chi phí giới
hạn trên mạng giao thông mởFile đính kèm:
 luan_an_mot_so_thuat_toan_tuan_tu_va_song_song_tren_mang_do.pdf
luan_an_mot_so_thuat_toan_tuan_tu_va_song_song_tren_mang_do.pdf

