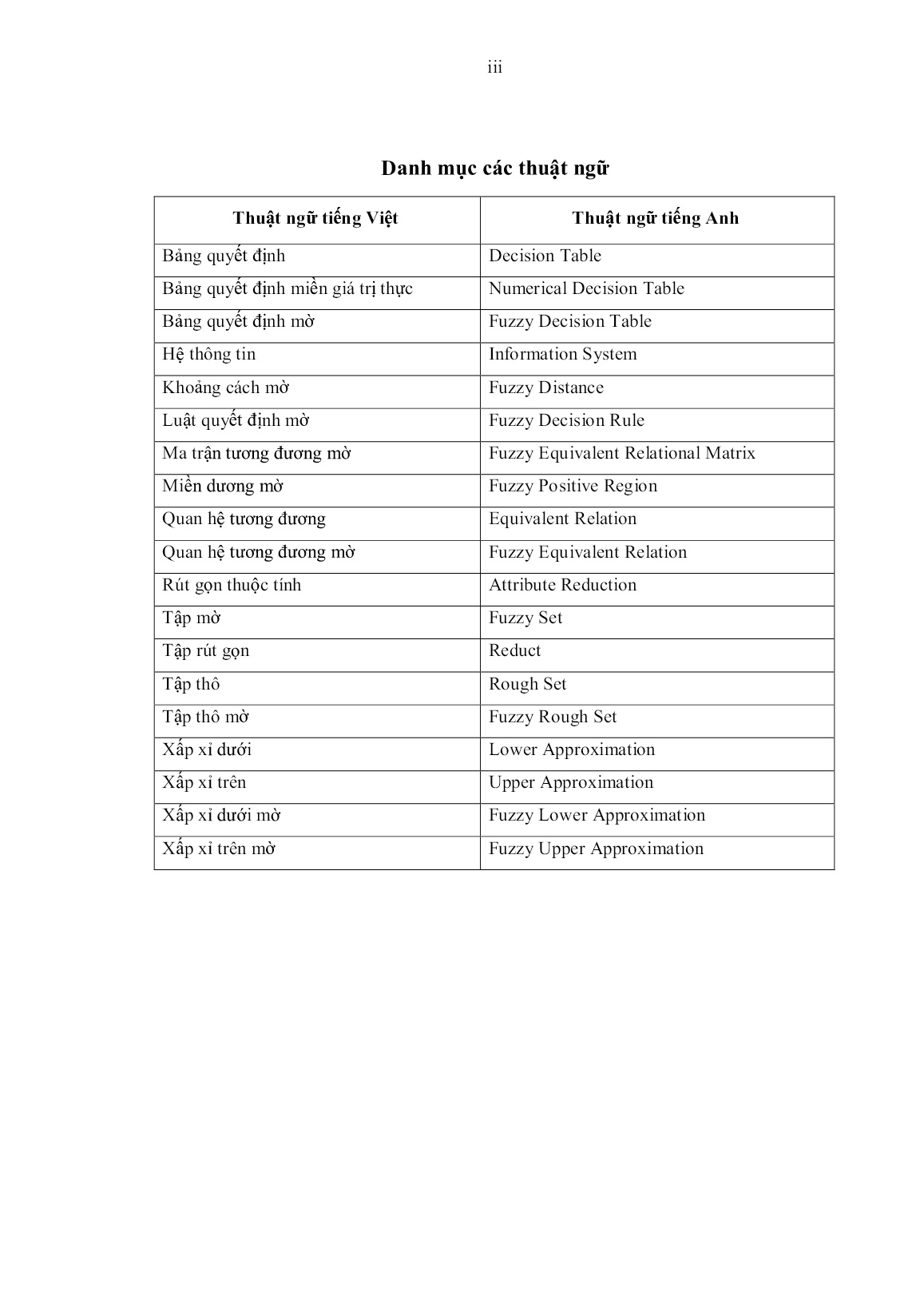
Luận án Nghiên cứu các phương pháp rút gọn thuộc tính và sinh luật quyết định theo tiếp cận tập thô mờ

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
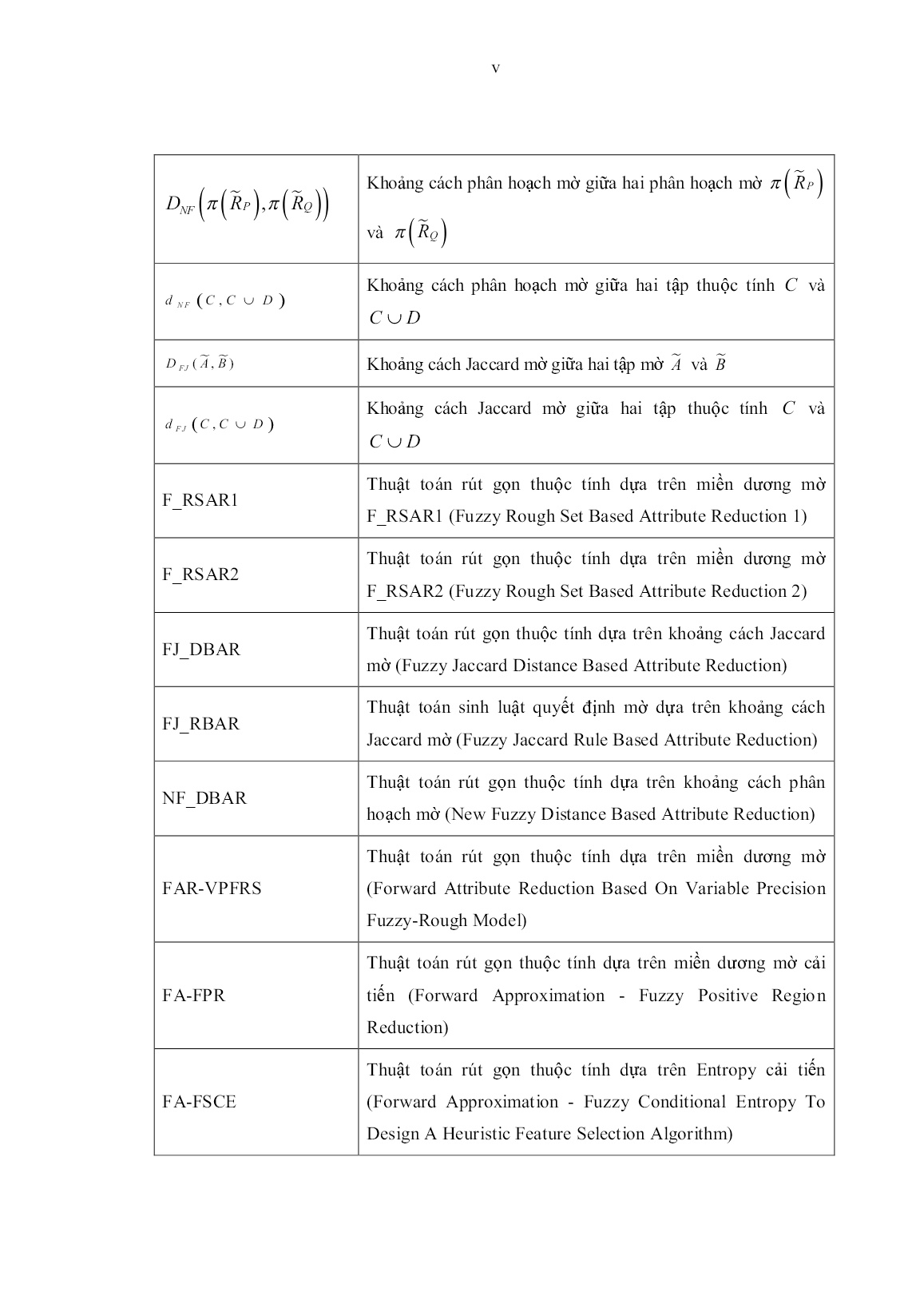
Trang 7

Trang 8
Trang 9
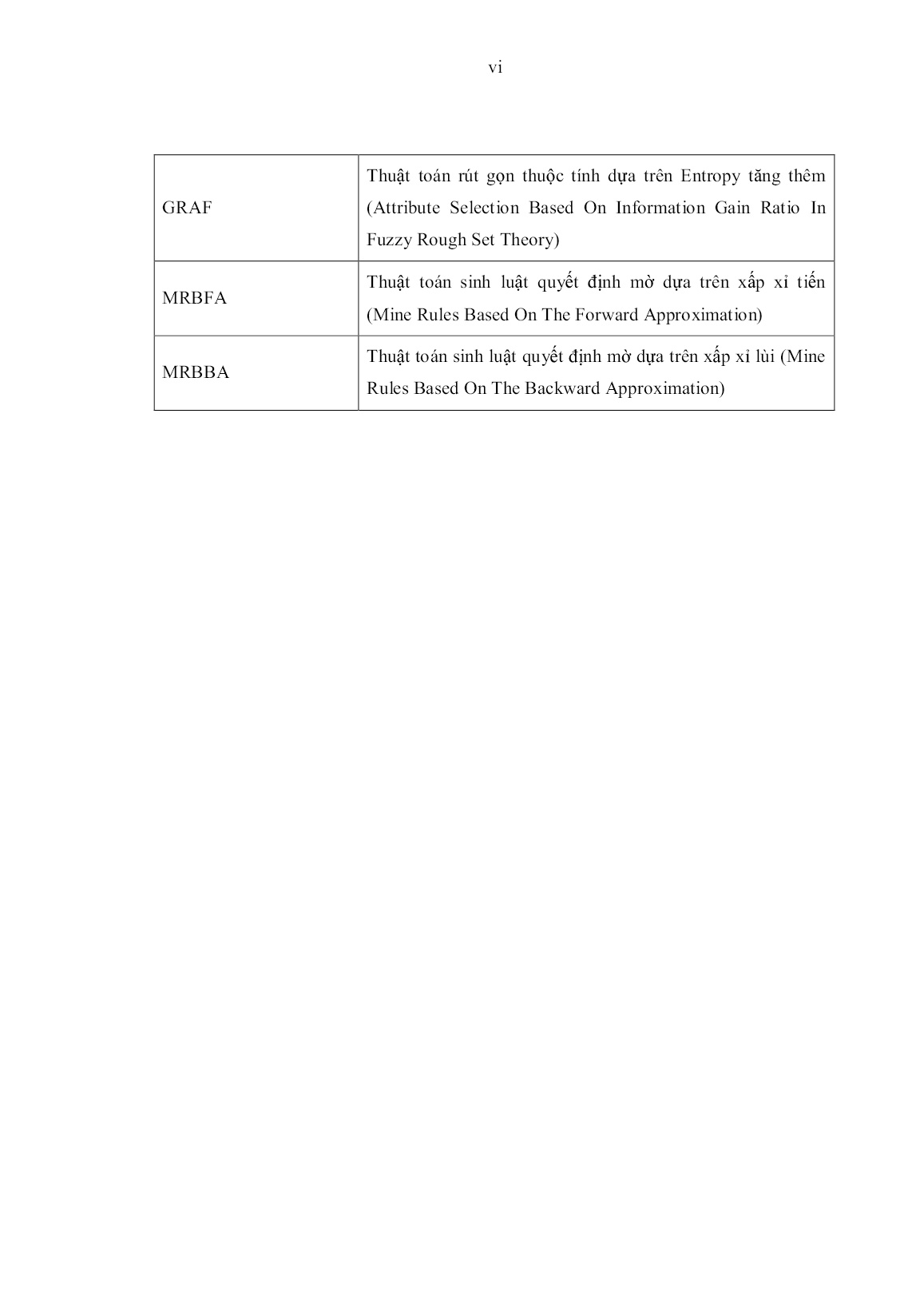
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Luận án Nghiên cứu các phương pháp rút gọn thuộc tính và sinh luật quyết định theo tiếp cận tập thô mờ", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Luận án Nghiên cứu các phương pháp rút gọn thuộc tính và sinh luật quyết định theo tiếp cận tập thô mờ

đó, bất đẳng thức (2.11) được chứng minh.
Tiếp theo, luận án xây dựng khoảng cách Jaccard mờ giữa hai phân
hoạch dựa trên ma trận tương đương mờ, áp dụng rút gọn thuộc tính của
bảng quyết định miền giá trị thực. Cho bảng quyết định DT U, C D với
U u,..., u và PC , giả sử u là một lớp tương đương chứa u trong
1 n i P i
phân hoạch UP/ . Khi đó, khoảng cách giữa tập thuộc tính C và CD
trong công trình [4] được xây dựng dựa trên khoảng cách Jaccard giữa hai
tập hợp hữu hạn như sau:
50
U u u
1 iCCD i
dJ C, C D 1 (2.19)
U i 1 u u
iCCD i
Sử dụng các phép toán trong [4] biến đổi độ đo khoảng cách trong công
thức (2.19) tương đương công thức (2.20) như sau:
UUu u u u u
1 iCCDCD i i 1 i i
dJ C, C D 1 1 (2.20)
UUi 1u() u u i 1 u
iCCDC i i i
Độ đo khoảng cách trong công thức (2.20) đặc trưng cho độ “gần
nhau” giữa tập thuộc tính điều kiện C và tập thuộc tính quyết định D và
được tác giả trong công trình [4] sử dụng để xây dựng phương pháp rút gọn
thuộc tính trong bảng quyết định. Sử dụng độ đo khoảng cách trong công
thức (2.20) kết hợp với công thức (2.9), luận án xây dựng độ đo khoảng cách
Jaccard mờ giữa hai phân hoạch mờ dựa trên ma trận tương đương mờ theo
hướng tiếp cận tập thô mờ.
Định nghĩa 2.4. Cho bảng quyết định mờ DT U, C D , giả sử hai quan
hệ tương đương mờ RC và RD xác định trên hai tập thuộc tính C và D tương
C D
ứng. Gọi rij là các phần tử của ma trận tương đương mờ MR C và rij là
các phần tử của ma trận tương đương mờ MR D với 1 i , j n . Dựa trên
công thức (2.20) và (2.9), luận án xây dựng độ đo khoảng cách Jaccard mờ
giữa hai tập thuộc tính C và CD dựa trên ma trận quan hệ tương đương
mờ như sau:
n
CD
U min rij , r ij
1 j 1
dFJ C, C D 1 n (2.21)
U i 1 C
rij
j 1
Mệnh đề 2.1. Cho bảng quyết định mờ DT U, C D và RC , RD là hai quan
hệ tương đương mờ xác định trên tập thuộc tính C, D. Khi đó ta có:
51
1) 0 dFJ C , C D 1 (2.22)
2) dFJ C, C D 0 khi RRCD (2.23)
Chứng minh:
1) Theo công thức tính khoảng cách mờ (2.21), dễ dàng nhận thấy
0 dFJ C , C D 1.
2) Theo tính chất của quan hệ tương đương mờ [40], [72] ta có:
CD
RRCD RCD x,, y R x y rij r ij i, j [1..n] . Thay vào công thức
(2.21) ta có dFJ C, C D 0 .
Mệnh đề 2.2. Cho bảng quyết định mờ DT U, C D và BC , khi đó ta
có dFJ B,, B D d FJ C C D .
Chứng minh: Theo [40], [72] ta có BC UCUB// (phân hoạch
UC/ mịn hơn phân hoạch UB/ ) khi và chỉ khi [][]uCB u .
Theo tính chất của quan hệ tương đương mờ [40], [72] và công thức
n n
(2.21) ta có [][]u u [][]u u CB
CB iRCRB ()() i rij r ij
i, j 1 i , j 1
n n DD DD
CB r r r r
r r . Do rCB, r [0,1] nên ij ij ij ij .
ij ij ij ij CB (1 CB ) (1 )
i, j 1 i , j 1 rij r ij rij r ij
Thay vào công thức tính khoảng cách mờ (2.21) có
dFJFJ(,)(,) B B D d C C D .
Khoảng cách Jaccard giữa hai phân hoạch mờ theo công thức (2.21)
được gọi là khoảng cách Jaccard mờ dựa trên ma trận tương đương mờ.
52
2.3.2. Phương pháp rút gọn thuộc tính sử dụng khoảng cách
Jaccard mờ
Trong phần này, luận án trình bày phương pháp rút gọn thuộc tính của
bảng quyết định miền giá trị thực sử dụng độ đo khoảng cách Jaccard mờ
dựa trên ma trận quan hệ tương đương mờ ở công thức (2.21). Cho bảng
quyết định miền giá trị thực DT U, C D với U x1, x 2 ,..., xn . Trên tập
thuộc tính điều kiện luận án sử dụng một quan hệ tương đương mờ xác định
trên miền giá trị thuộc tính như ở công thức (1.11).
Trên tập thuộc tính quyết định luận án sử dụng quan hệ tương đương
IND D với ma trận tương đương M IND D d , d 1 nếu
ij n n ij
x x và d 0 nếu x x . Nói cách khác, lớp tương đương x có
j i D ij j i D i D
thể xem là lớp đương đương mờ, ký hiệu là xi , với hàm thuộc x x j 1
D i D
nếu xj x i và x x j 0 nếu xj x i . Khi đó, ký hiệu phân hoạch mờ
D i D D
n
D x x ,..., x .
iDDDi 1 1 n
Tương tự phương pháp rút gọn thuộc tính sử dụng khoảng cách
Jaccard trong lý thuyết tập thô truyền thống, phương pháp đề xuất bao gồm
các bước: Định nghĩa tập rút gọn dựa trên khoảng cách Jaccard mờ, định
nghĩa độ quan trọng của thuộc tính và xây dựng thuật toán heuristic tìm một
tập rút gọn không dư thừa dựa trên tiêu chuẩn độ quan trọng của thuộc tính.
Định nghĩa 2.5. Cho bảng quyết định có miền giá trị thực DT U, C D và
tập thuộc tính PC . Nếu
1) dFJFJ P,, P D d C C D (2.24)
2) pPdPpPp ,(,)(,)FJ DdCCD FJ (2.25)
thì P là một tập rút gọn của C dựa trên khoảng cách Jaccard mờ.
53
Định nghĩa 2.6. Cho bảng quyết định DT U, C D , PC và b C P .
Độ quan trọng của thuộc tính b đối với P được định nghĩa bởi
SIGbPFJFJ d PPDd,, P bP b D (2.26)
Độ quan trọng của thuộc tính đặc trưng cho sự phụ thuộc của thuộc
tính điều kiện vào thuộc tính quyết định và được sử dụng làm tiêu chuẩn lựa
chọn thuộc tính cho thuật toán heuristic tìm tập rút gọn sau đây.
Thuật toán FJ_DBAR (Fuzzy Jaccard Distance based Attribute
Reduction): Thuật toán heuristic tìm một tập rút gọn sử dụng khoảng cách
Jaccard mờ.
Đầu vào: Bảng quyết định miền giá trị thực DT U, C D , quan hệ
tương đương mờ R .
Đầu ra: Một tập rút gọn P .
// Khởi tạo tập rút gọn bằng rỗng
1. P ; MR(P ) 0 ; dFJ , D 1;
2. Tính MR()C , M (IND(D)) ;
3. Tính dFJ C, C D ;
// Thêm dần vào P các thuộc tính có độ quan trọng lớn nhất
4. While dFJ P,, P D d FJ C C D Do
5. Begin
6. For each a C P Do
7. Begin
8. Tính dFJ P a, P a D ;
9. Tính SIGaPFJFJ d PPDd,, P aP a D ;
// Tính độ quan trọng của từng thuộc tính điều kiện còn
lại với tập thuộc tính quyết định
10. End;
54
11. Chọn am C P sao cho SIGP a m Max SIG P a ;
a C P
// Chọn thuộc tính có độ quan trọng lớn nhất theo khoảng cách
Jaccard mờ kết nạp vào tập rút gọn
12. P P am ;
13. Tính dFJ P, P D ;
14. End;
//Loại bỏ các thuộc tính dư thừa trong P nếu có
15. For each a P
16. Begin
17. Tính dFJ P a, P a D ;
18. If dFJ P a,, P a D d FJ C C D then P P a;
// Loại bỏ những thuộc tính không cần thiết đến điều kiện xây
dựng tập rút gọn
19. End;
20. Return P ;
Ví dụ 2.3. Cho bảng quyết định miền giá trị thực DT U, C D (Bảng 2.1)
với U u1,,,,, u 2 u 3 u 4 u 5 u 6 , C c1,,,,, c 2 c 3 c 4 c 5 c 6 .
Bảng 2.1. Bảng quyết định miền giá trị thực
U c1 c2 c3 c4 c5 c6 D
u1 0.8 0.2 0.6 0.4 1 0 0
u2 0.8 0.2 0 0.6 0.2 0.8 1
u3 0.6 0.4 0.8 0.2 0.6 0.4 0
u4 0 0.4 0.6 0.4 0 1 1
u5 0 0.6 0.6 0.4 0 1 1
u6 0 0.6 0 1 0 1 0
55
Áp dụng các bước của thuật toán FJ_DBAR, sử dụng quan hệ tương
đương mờ theo công thức (1.11).
P , MR(P ) 0 , dFJ , D 1, tính các ma trận tương đương
mờ MR(c1 ),( MR c 2 ),( MR c 3 ),( MR c 4 ),( MR c 5 ),( MR c 6 ),( MR C ),( MINDD ) .
1 1 0 0 0 0 1 1 0 0 0 0
1 1 0 0 0 0
1 1 0 0 0 0
0 0 1 0 0 0 0 0 1 1 0 0
c
MR()1 , M (Rc2 )
0 0 0 1 1 1 0 0 1 1 0 0
0 0 0 1 1 1 0 0 0 0 1 1
0 0 0 1 1 1 00 0 0 1 1
1 0 0 1 1 0 1 0 0 1 1 0
0 1 0 0 0 1
0 1 0 0 0 0
0 0 1 0 0 0 0 0 1 0 0 0
c
MR()3 , M (Rc4 )
1 0 0 1 1 0 1 0 0 1 1 0
1 0 0 1 1 0 1 0 0 1 1 0
0 1 0 0 0 1 00 0 0 0 1
1 0 0 0 0 0 1 0 0 0 0 0
0 1 0 0.2 0.2 0.2 0 1 0 0.2 0.2 0.2
0 0 1 0 0 0 0 0 1 0 0 0
M ()Rc5 , M ()Rc6
0 0.2 0 1 1 1 0 0.2 0 1 1 1
0 0.2 0 1 1 1 0 0.2 0 1 1 1
0 0.2 0 1 1 1 0 0.2 0 1 1 1
1 0 0 0 0 0 1 0 1 0 0 1
0 1 0 0 0 0 0 1 0 1 1 0
0 0 1 0 0 0 1 0 1 0 0 1
MR(),C M() IND D .
0 0 0 1 0 0 0 1 0 1 1 0
0 0 0 0 1 0 0 1 0 1 1 0
0 0 0 0 0 1 1 0 1 0 0 1
Tính:
dFJ C, C D 0, dFJ { c1 },{ c 1 } { D } 0.38889;
56
dFJ { c2 },{ c 2 } {} D 0.5; dFJ { c3 },{ c 3 } { D } 0.389;
dFJ { c4 },{ c 4 } { D } 0.222; dFJ { c5 },{ c 5 } { D } 0.23958;
dFJ { c6 },{ c 6 } { D } 0.23958.
SIGP { c1} 0.6111 1; SIGP { c2} 0. 5 ; SIGP {} c3 0.611 ;
SIGP {} c4 0.778 ; SIGP {} c5 0.76042 ; SIGP {} c6 0.76042 .
Thuộc tính c4 được chọn và P c4 .
Tính tương tự, ta có: dFJ {,} c4 c 1,{ c 4 , c 1 } { D } 0 , kiểm tra
dFJ { c4 , c 1 },{ c 4 , c 1 } D d FJ C , C D 0 , thuật toán dừng và kết luận
P c4, c 1 . Sau khi kiểm tra tính dư thừa, kết luận P c4, c 1 là tập rút gọn
của DT.
Thuật toán FJ_DBAR tìm được một tập rút gọn và kiểm tra tính dư
thừa của tập rút gọn. Độ phức tạp tính toán ma trận tương đương mờ của một
2
thuộc tính là OU() với U số lượng đối tượng, C là số lượng thuộc tính điều
2
kiện; độ phức tạp tính toán của MR()C là OCU() . Thuật toán có hai vòng
lặp lồng nhau theo số lượng của thuộc tính điều kiện. Do vậy, độ phức tạp
tính toán của FJ_DBAR là OCU()3 2 .
2.3.3. Thử nghiệm và đánh giá kết quả
Luận án lựa chọn thuật toán heuristic tìm một tập rút gọn dựa trên
lượng thông tin tăng thêm GAIN_RATIO_AS_FRS [24] (gọi là GRAF) khi
thêm một thuộc tính vào tập rút gọn để so sánh với thuật toán FJ_DBAR về
thời gian thực hiện, tập rút gọn và độ chính xác phân lớp dữ liệu. Thuật toán
GRAF tính toán độ quan trọng của thuộc tính dựa trên entropy mờ. Để tiến
hành thực nghiệm, luận án thực hiện các công việc sau:
1) Cài đặt thuật toán GRAF [24] và thuật toán FJ_DBAR bởi ngôn ngữ
C#. Cả hai thuật toán đều sử dụng quan hệ tương đương mờ định nghĩa ở
57
công thức (1.11) ở các thuộc tính điều kiện, trên tập thuộc tính quyết định sử
dụng quan hệ tương đương mờ như ở công thức (1.12).
2) Trên máy tính PC với cấu hình: Bộ xử lý Pentium Core i3, 2.4 GHz
CPU, 2 GB RAM, sử dụng hệ điều hành Windows 10, chạy thử nghiệm các
thuật toán trên sáu bộ dữ liệu lấy từ kho dữ liệu UCI [99] như ở Bảng 2.2.
Với mỗi bộ dữ liệu, ký hiệu U là số lượng các đối tượng, R là số lượng
thuộc tính của tập rút gọn, C là số lượng các thuộc tính điều kiện, t là thời
gian thực hiện của thuật toán (tính bằng giây), các thuộc tính điều kiện ký
hiệu là 1, 2, ..., C .
Bảng 2.2. Bộ dữ liệu thử nghiệm
Số thuộc tính Số đối
TT Bộ dữ liệu Số lớp
điều kiện tượng
1 Fisher_Order 35 47 4
2 Iris 4 150 3
3 Glass 10 214 7
4 Sonar 60 208 2
5 Sensor_Readings_24 24 5456 4
6 EEG_Eye_State 14 14980 2
Thời gian thực hiện và tập rút gọn thu được của hai thuật toán được
miêu tả trong Bảng 2.6 và Bảng 2.7.
Bảng 2.6. Kết quả thực nghiệm của FJ_DBAR và GRAF
FJ_DBAR GRAF
TT Tập dữ liệu |U| |C|
|R| t |R| t
1 Fisher_Order 47 35 18 0.095 21 0.107
2 Iris 150 4 1 0.002 2 0.003
3 Glass 214 10 6 0.46 8 0.48
4 Sonar 208 60 26 2.053 23 1.980
58
5 Sensor_Readings_24 5456 24 14 2.095 12 1.986
6 EEG_Eye_State 14980 14 7 2.580 7 2.790
Kết quả thực nghiệm ở Bảng 2.6 cho thấy số lượng thuộc tính của tập
rút gọn thu được của FJ_DBAR và GRAF phụ thuộc vào từng bộ dữ liệu cụ
thể. Thuật toán FJ_DBAR tìm được tập rút gọn có số lượng thuộc tính nhỏ
hơn GRAF tại 3/6 bộ dữ liệu thử nghiệm (Fisher_Order, Iris, Glass), bằng
nhau ở tại 1/6 bộ dữ liệu thử nghiệm (EEG_Eye_State), lớn hơn GRAF tại
2/6 bộ dữ liệu (Sonar, Sensor_Readings_24). Thời gian thực hiện của
FJ_DBAR nhanh hơn GRAF tại 4/6 bộ dữ liệu (Fisher_Order, Iris, Glass,
EEG_Eye_State). Trên một số bộ dữ liệu thử nghiệm, thuật toán nào tìm
được tập rút gọn có số lượng thuộc tính ít hơn thì có thời gian thực hiện
nhanh hơn. Tại bộ dữ liệu (EEG_Eye_State) tìm được tập rút gọn giống nhau
theo hai thuật toán thì FJ_DBAR có thời gian thực hiện nhanh hơn, điều này
phù hợp với lý thuyết bởi có cùng độ phức tạp tính là OCU()3 2 nhưng công
thức tính độ quan trọng của thuộc tính của GRAF [24] tiếp cận theo hướng
entropy mờ có sử dụng biểu thức Logarit sẽ mất thời gian tính toán hơn so
với FJ_DBAR. Biểu đồ so sánh thời gian thực hiện của FJ_DBAR và GRAF
được thể hiện như Hình 2.3
3
2.5
2
1.5
1 FJ_DBAR
0.5 GRAF
0
Hình 2.3. Thời gian thực hiện của FJ_DBAR và GRAF
59
Các tập rút gọn cụ thể của FJ_DBAR và GRAF trên sáu bộ số liệu thực
nghiệm thể hiện ở Bảng 2.7.
Bảng 2.7. Tập rút gọn thu được bởi FJ_DBAR và GRAF
TT Bộ dữ liệu FJ_DBAR GRAF
{22,11,13,14,15,16,17,18,19
{11,13,14,15,16,17,18,19,29,3
1 Fisher_Order ,29,30,31,32,33,34,9,20,5,2
0,31,32,33,34,28,24,12,2}
5,10,3}
2 Iris {3} {3,4}
3 Glass {2,1,3,4,5,10} {2,1,3,4,6,10,8,7}
{21,36,27,12,31,54,24,22,33,2 {21,36,30,12,27,54,41,22,32
4 Sonar 9,57,48,39,34,6,46,20,16,7,11, ,57,39,16,46,34,6,11,10,31,
26,50,8,10,56,58} 8,26,56,48,58}
{4,3,7,2,15,5,10,23,8,6,14,11, {3,7,12,15,5,21,24,8,14,17,1
5 Sensor_Readings_24
1,9} ,16}
6 EEG_Eye_State {8,11,2,3,12,10,5} {8,11,2,3,12,10,5}
Tiếp theo, luận án thực hiện việc so sánh độ chính xác phân lớp dữ
liệu của tập rút gọn thu được bởi FJ_DBAR và GRAF. Độ chính xác phân
lớp dữ liệu của các tập rút gọn được đánh giá bằng thuật toán C4.5 trong
công cụ J48 của WEKA [100]. Để thực hiện việc đánh giá độ chính xác phân
lớp dữ liệu, luận án chia tập dữ liệu thử nghiệm thành mười phần bằng nhau;
chín phần mười tập dữ liệu được dùng làm dữ liệu huấn luyện, một phần
mười dùng làm dữ liệu kiểm tra. Kết quả thực nghiệm được thể hiện ở Bảng
2.8.
Bảng 2.8. Độ chính xác phân lớp C4.5 của FJ_DBAR và GRAF
FJ_DBAR GRAF
Độ chính Độ chính
TT Tập dữ liệu |U| |C|
|R| xác phân |R| xác phân
lớp (%) lớp (%)
1 Fisher_Order 47 35 18 78.72 21 76.59
60
2 Iris 150 4 1 94.00 2 94.00
3 Glass 214 10 6 80.15 8 81.70
4 Sonar 208 60 26 71.63 23 70.67
5 Sensor_Readings_24 5456 24 14 94.84 12 91.25
6 EEG_Eye_State 14980 14 7 81.25 7 81.25
Kết quả thực nghiệm trên sáu bộ dữ liệu ở Bảng 2.8 chỉ ra rằng độ
chính xác phân lớp dữ liệu theo thuật toán C4.5 của FJ_DBAR cao hơn
GRAF tại 3/6 bộ dữ liệu (Fisher_Order, Sonar, Sensor_Readings_24), bằng
nhau tại 2/6 bộ dữ liệu (Iris, EEG_Eye_State), thấp hơn tại 1/6 bộ dữ liệu
(Glass). Do vậy, luận án kết luận FJ_DBAR có độ chính xác phân lớp cao
hơn GRAF trên một số bộ dữ liệu thử nghiệm, với những bộ dữ liệu có tập
rút gọn giống nhau thì độ chính xác phân lớp theo thuật toán C4.5 của hai
thuật toán là như nhau. Độ chính xác phân lớp này phụ thuộc vào tập rút gọn
thu được theo các phương pháp với những bộ dữ liệu cụ thể, không phụ
thuộc vào số lượng thuộc tính của tập rút gọn. Có những bộ dữ liệu có số
lượng thuộc tính của tập rút gọn giống nhau nhưng các thuộc tính cụ thể khác
nhau thì độ chính xác phân lớp theo thuật toán C4.5 có thể cũng khác nhau.
Ví dụ bộ Iris với tập rút gọn thu được theo thuật toán FJ_DBAR là thuộc tính
{3} thì độ chính xác phân lớp là 94%, với tập rút gọn thu được theo thuật
toán F_RSAR2 là thuộc tính {4} thì độ chính xác 94.67%. Ngoài ra, độ chính
xác phân lớp của các tập rút gọn theo thuật toán C4.5 còn phụ thuộc vào tỷ lệ
phân chia tập dữ liệu giữa phần huấn luyện và phần kiểm tra. Thông thường,
các phương pháp hay lựa chọn chia tập dữ liệu thành mười phần hoặc ba
phần bằng nhau; một phần sử dụng làm dữ liệu huấn luyện, các phần còn lại
sử dụng làm dữ liệu kiểm tra. Biểu đồ so sánh độ chính xác phân lớp của
FJ_DBAR và GRAF theo C4.5 được thể hiện như Hình 2.4.
61
100.00 94 94.84
90.00
78.72 80.15 81.25
80.00 71.63
70.00
60.00
50.00
40.00 FJ_DBAR
30.00
GRAF
20.00
10.00
0.00
Hình 2.4. Độ chính xác phân lớp C4.5 của FJ_DBAR và GRAF
Bằng thực nghiệm, luận án kết luận thuật toán toán FJ_DBAR có khả
năng cho kết quả tốt hơn GRAF về thời gian thực hiện và độ chính xác phân
lớp dữ liệu trên một số bộ dữ liệu thử nghiệm.
2.4. Kết luận chương 2
Một trong những mục tiêu của rút gọn thuộc tính trong bảng quyết
định là nâng cao độ chính xác phân lớp của dữ liệu. Trên lớp bài toán rút gọn
thuộc tính trong bảng quyết định miền giá trị thực, các nghiên cứu liên quan
cho thấy các phương pháp rút gọn thuộc tính theo tiếp cận tập thô mờ có độ
chính xác phân lớp cao hơn phương pháp rút gọn thuộc tính theo tiếp cận tập
thô truyền thống [24], [39], [44], [47], [72], [80]. Chương 2 của luận án cải
tiến phương pháp rút gọn thuộc tính của bảng quyết định miền giá trị thực sử
dụng miền dương mờ trong công trình của Hu, Q., [38] để tìm một tập rút
gọn không dư thừa thuộc tính, bảo toàn miền dương mờ dựa trên quan hệ
tương đương mờ. Bên cạnh đó, phương pháp đề xuất cũng cải tiến công thức
tính độ quan trọng của thuộc tính sử dụng làm tiêu chuẩn lựa chọn thuộc tính
cho tập rút gọn để giảm bớt thời gian tính toán độ quan trọng của thuộc tính.
62
Đóng góp chính của Chương 2 là đề xuất phương pháp rút gọn thuộc tính
trực tiếp trên bảng quyết định miền giá trị thực sử dụng khoảng cách Jaccard
mờ. Khoảng cách Jaccard mờ được xây dựng dựa trên khoảng cách Jaccard
giữa hai tập hợp và chứng minh đầy đủ các tính chất của khoảng cách. Kết
quả thử nghiệm trên một số bộ dữ liệu mẫu từ kho dữ liệu UCI [99] cho thấy,
độ chính xác phân lớp của phương pháp sử dụng khoảng cách Jaccard mờ tốt
hơn độ chính xác phân lớp của phương pháp sử dụng entropy mờ trên một số
bộ dữ liệu thực nghiệm, thời gian thực hiện của phương pháp khoảng cách
nhanh hơn entropy trên đa số bộ dữ liệu thử nghiệm.
63
CHƯƠNG 3. RÚT GỌN THUỘC TÍNH TRONG BẢNG QUYẾT
ĐỊNH MIỀN GIÁ TRỊ THỰC SỬ DỤNG KHOẢNG CÁCH PHÂN
HOẠCH MỜ
Tiếp nối sự thành công của kỹ thuật sử dụng khoảng cách Jaccard mờ
trong phần trước, Chương 3 của luận án đề xuất một độ đo khoảng cách
giữa hai phân hoạch mờ, gọi là khoảng cách phân hoạch mờ. Dựa trên
khoảng cách phân hoạch mờ đề xuất, chương này xây dựng phương pháp rút
gọn thuộc tính của bảng quyết định miền giá trị thực. Thử nghiệm trên một
số bộ dữ liệu cho thấy, phương pháp đề xuất hiệu quả hơn phương pháp sử
dụng entropy thông tin mờ và phương pháp sử dụng miền dương mờ theo
tiêu chí đánh giá độ chính xác phân lớp dữ liệu và thời gian thực hiện của
thuật toán.
3.1. Đặt vấn đề
Chương 2 của luận án cho thấy sự hiệu quả của phương pháp rút gọn
thuộc tính trực tiếp trên bảng quyết định miền giá trị thực sử dụng khoảng
cách Jaccard mờ. Thực nghiệm trên một số bộ dữ liệu lấy từ kho dữ liệu UCI
[99] thấy rằng kỹ thuật sử dụng khoảng cách Jaccard mờ tỏ ra hiệu quả so
với phương pháp sử dụng entropy mờ dựa trên các tiêu chí đánh giá về thời
gian thực hiện và độ chính xác phân lớp dữ liệu. Với mục tiêu nghiên cứu
các phương pháp hiệu quả để rút gọn thuộc tính của bảng quyết định miền
giá trị thực, bổ sung làm phong phú thêm bộ sưu tập các phương pháp, nhằm
đánh giá một cách khái quát hơn về nhóm phương pháp sử dụng khoảng cách
mờ theo tiếp cận tập thô mờ. Chương 3 của luận án đề xuất độ đo khoảng
cách giữa hai phân hoạch mờ và ứng dụng rút gọn thuộc tính của bảng quyết
định miền giá trị thực. Thực nghiệm trên một số bộ số liệu lấy từ kho dữ liệu
UCI [99] chỉ ra rằng, phương pháp sử dụng khoảng cách phân hoạch mờ tỏ ra
hiệu quả hơn phương pháp sử dụng pháp sử dụng entropy thông tin mờ [24],
[38]-[40], [88], [89] và miền dương mờ [9], [38]-[40], [72] trên một số bộ dữ
64
liệu thử nghiệm theo tiêu chí đánh giá thời gian thực hiện thuật toán và độ
chính xác phân lớp dữ liệu. Qua đó, khẳng định được sự thành công của
phương pháp sử dụng khoảng cách mờ trong rút gọn thuộc tính của bảng
quyết định miền giá trị thực, là sự tiếp nối của phương pháp sử dụng khoảng
cách trong tập thô truyền thống.
Các kết quả chính trong chương này được công bố trong công trình
[CCN4].
3.2. Khoảng cách phân hoạch mờ và các tính chất
Trong hệ thông tin, mỗi tập thuộc tính sinh ra một tri thức về tập các
đối tượng, trong đó mỗi phần tử của tri thức là một lớp tương đương, hay
một khối. Khoảng cách cho phép đánh giá độ gần nhau (hay độ tương
đương) giữa các tri thức, nghĩa là khoảng cách giữa hai tri thức càng nhỏ
thì hai tri thức đó càng gần nhau, hay càng tương đương nhau và ngược lạFile đính kèm:
 luan_an_nghien_cuu_cac_phuong_phap_rut_gon_thuoc_tinh_va_sin.pdf
luan_an_nghien_cuu_cac_phuong_phap_rut_gon_thuoc_tinh_va_sin.pdf TOMTAT_LUANAN_CCNGHIA.pdf
TOMTAT_LUANAN_CCNGHIA.pdf Trang thong tin LATS tieng Anh_CCNGHIA.pdf
Trang thong tin LATS tieng Anh_CCNGHIA.pdf Trang thong tin LATS tieng Viet_CCNGHIA.pdf
Trang thong tin LATS tieng Viet_CCNGHIA.pdf

