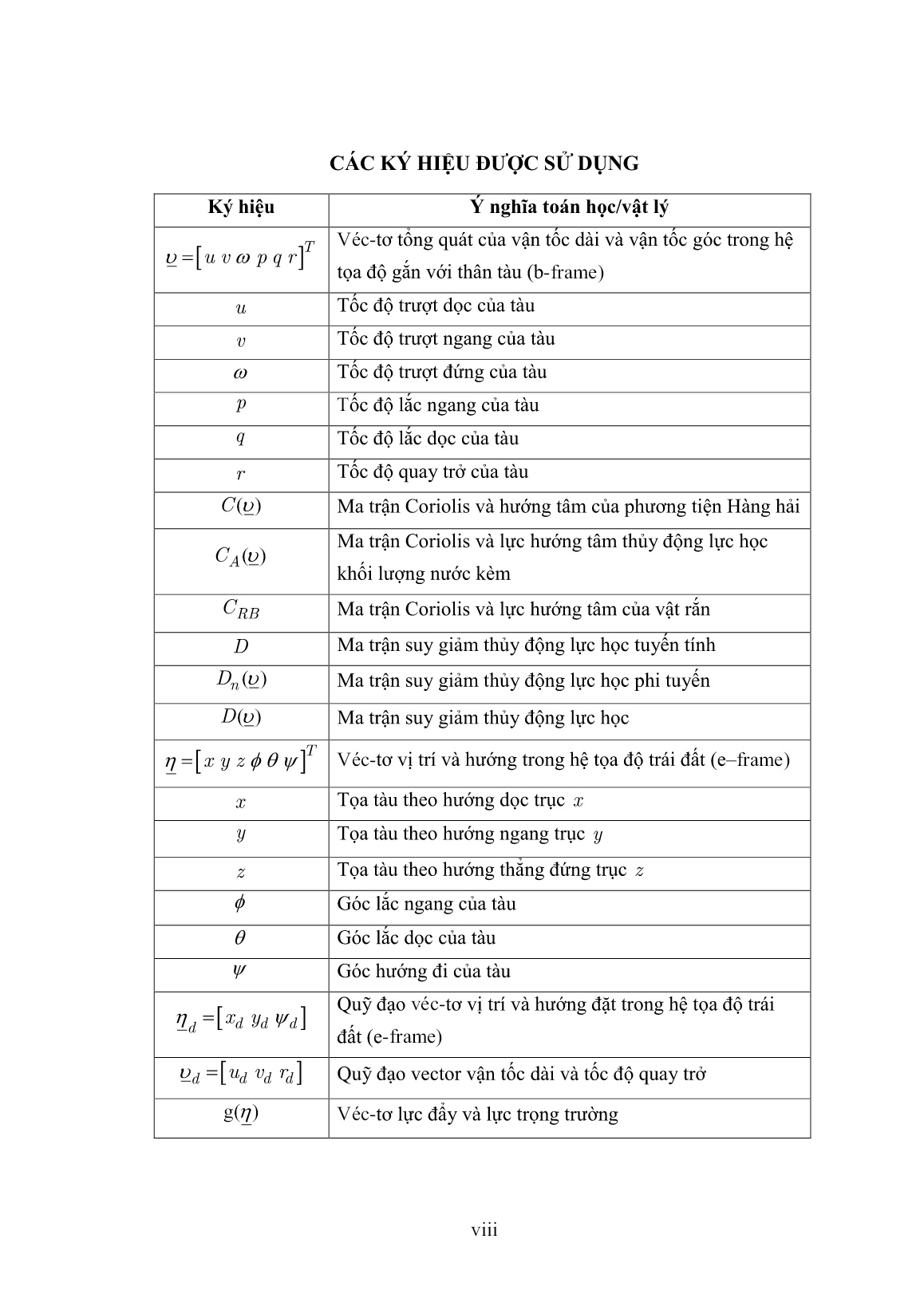
Luận án Nghiên cứu giải pháp điều khiển bám quỹ đạo tàu thủy có ràng buộc tín hiệu và bất định hàm ở đầu vào

n phản hồi 
đầu ra: 
 45 
 TT 1
 uk u k 1 I,0,...,0 k Q k k R k k Q k br k k (2.36) 
với được xác định theo (2.31) và 
 kk 00 kk
 0 2
 k k k k k kk
 k , bkkz
 p * (2.37) 
 NN 12 N
 k k k k k k k k kk
 rk
 k A(), zk k B (), z k k C (). z k
2.2 Các phƣơng pháp tối ƣu hóa có ràng buộc 
 Trong bộ điều khiển dự báo có thành phần tối ưu hóa Hình 2.1a với nhiệm vụ 
tìm nghiệm của bài toán tối ưu (2.8) thỏa mãn ràng buộc P . Nó được thực hiện 
trong từng vòng lặp. Một cách tổng quát thì bài toán này có dạng chung cho tất cả 
các vòng lặp là: 
 n
 p* argmin J ( p ) với P p R i () p 0, i 1,2, , m (2.38) 
 pP 
trong đó i ()p – các hàm mô tả điều kiện ràng buộc. 
2.2.1 Những phƣơng pháp tối ƣu hóa có ràng buộc thƣờng sử dụng 
 Để giải quyết các bài toán tối ưu hóa có ràng buộc thông thường sử dụng hai 
phương pháp chính là phương pháp tối ưu truyền thống và phương pháp tối ưu tiến 
hóa. 
2.2.1.1 Phƣơng pháp tối ƣu hóa truyền thống 
 Những phương pháp truyền thống đều là phương pháp line search, nội dung 
chi tiết của phương pháp này đã được trình bày trong các tài liệu [5], [11]. Hai 
phương pháp line search cơ bản trong số chúng là SQP (sequential quadratic 
optimization) và phương pháp điểm trong (interior point). Đặc điểm của các phương 
pháp line search nói chung và hai phương pháp SQP, phương pháp điểm trong nói 
riêng là lần lượt tìm dãy các điểm p P, k 0,1, sao cho chúng hội tụ tới 
 k
nghiệm . Hiện nay, thuật toán SQP và „điểm trong‟ đã được cài đặt thành lệnh 
 46 
fmincon() với options chuẩn trong MatLab là „sqp‟ và fmincon() với options 
chuẩn trong MatLab là „interior-point‟. 
2.2.1.2 Phƣơng pháp tối ƣu tiến hóa 
 Các phương pháp tối ưu tiến hóa (evolutional optimization) cho bài toán tối ưu 
có ràng buộc (2.38) cũng được xây dựng trên cơ sở lặp từng bước, giống như line 
search, song quy luật tìm kiếm được sao chép từ phản ứng tự nhiên của sinh/động 
vật, thay vì xác định hướng tìm và khoảng cách bước tìm của toán học. Có rất nhiều 
phiên bản tối ưu tiến hóa khác nhau, nhưng có thể nói, chúng đều có gốc gác từ hai 
phương pháp chính là giải thuật di truyền (Genetic Algorithm - GA) và tối ưu bày 
đàn (Particle Swarm Optimization - PSO). Nội dung chi tiết của phương pháp này 
đã được trình bày trong các tài liệu [12], [37], [42]. Hiện nay, thuật toán „GA‟ và 
„PSO‟ đã được cài đặt chuẩn thành lệnh ga() và particleswarm() trong MatLab. 
2.2.2 Giải pháp điều khiển tối ƣu hóa có ràng buộc với bộ điều khiển MPC 
 Các phương pháp giải quyết bài toán tối ưu hóa có ràng buộc đề cập ở trên 
mặc dù sử dụng rất thuận tiện khi các phương pháp đó đã được cụ thể hóa bằng lệnh 
trong Matlab. Tuy nhiên, đối với bộ điều khiển theo nguyên lý receding horizon như 
MPC thì mỗi vòng lặp của bộ điều khiển phải giải bài toán tối ưu một lần, điều này 
có thể dẫn tới thời gian tính toán lệnh tối ưu hóa có ràng buộc vượt quá khoảng thời 
gian cho phép thực hiện một vòng lặp tức là khoảng thời gian ttkk 1 . Bởi vậy, để 
đơn giản sau đây luận án sẽ sử dụng kỹ thuật ước lượng xấpQk xỉ đã được giới thiệu 
trong [2], [5] để giải quyết bài toán tối ưu có ràng buộc. Kỹ thuật này được xây 
dựng dựa trên nhận xét rằng tín hiệu điều khiển trong (2.25) thay đổi theo từng 
 uk
vòng lặp với k 0,1,2... và phụ thuộc vào việc chọn ma trận xác định dương RQkk, 
như sau: 
 Nếu ma trận đối xứng xác định dương được chọn có chuẩn Qk càng lớn, 
 sai số bám sẽ càng nhỏ và gián tiếp kéo theo nghiệm tối ưu ut() có ut() càng 
 lớn. 
 47 
 Ngược lại, khi ma trận đối xứng xác định dương được chọn có chuẩn Rk 
 càng lớn, nghiệm tối ưu tìm được sẽ có càng nhỏ, gián tiếp kéo theo 
 sai lệch bám càng lớn và hệ hội tụ càng chậm. 
 Do đó trong trường hợp tín hiệu điều khiển bị ràng buộc, chẳng hạn như: 
 a u() t b (2.39) 
thì có thể hiệu chỉnh giá trị thích hợp theo từng vòng lặp để điều kiện (2.39) 
được thỏa mãn. Giải pháp này sẽ được luận án áp dụng để giải quyết điều kiện ràng 
buộc tín hiệu điều khiển như luận án đã đặt ra. 
2.3 Thiết kế bộ điều khiển MPCab  điều khiển chuyển động tàu bám quỹ đạo 
 đặt, có ràng buộc tín hiệu điều khiển khi mô hình tàu xác định 
 Như đã đề cập trong chương 1 của luận án, mô hình xác định của tàu thủy ba 
bậc tự do thiếu cơ cấu chấp hành là mô hình có cấu trúc xác định, các tham số trong 
mô hình là xác định và mô hình coi như không có nhiễu tác động. Mục tiêu và 
nhiệm vụ của luận án là từ mô hình xác định, thiết kế bộ điều khiển chuyển động 
tàu thủy bám theo quỹ đạo đặt và có ràng buộc tín hiệu điều khiển. 
 Mô hình động lực học tàu thủy ba bậc tự do, thiếu cơ cấu chấp hành trên mặt 
phẳng ngang dạng mô hình xác định (không chứa thành phần bất định) theo [21] có 
cấu trúc như sau: 
 33
  J (  )  ,  RR ,  
 Rk (2.40) 
 M C(  ) D (  )  g (  ) F  ,  2 , F 3 2
 r  R R
  F
trong đó là ma trận có số cột ít hơn số hàng (đặc điểm của hệ thiếu cơ cấuRQ kkchấp, 
hành). Nhiệm vụ điều khiển là xây dựng được bộ điều khiển để đầu ra của hệ 
bám theo được quỹ đạo mẫu  ()()t w t cho trước, đồng thời thỏa mãn các điều 
 d
kiện ràng buộc . Đối với độ lớn góc bẻ lái trên tàu thủyut() đượcut qui() định, 
 gh   gh , với là góc bẻ lái, gh là giới hạn góc bẻ lái. Điều kiện ràng 
buộc này tương đương với ràng buộc về mô-men giới hạn quay trở như sau: 
 r.. gh  r  r gh (2.41) 
 48 
trong đó r. gh – giá trị giới hạn đặt mô-men của bánh lái (giá trị này tỷ lệ với độ lớn 
của góc bẻ lái và coi như tương đương với ràng buộc về độ lớn góc bẻ lái). 
 Để giải quyết nhiệm vụ đặt ra, luận án sẽ sử dụng nguyên lý điều khiển dự báo 
MPC trên cơ sở tuyến tính hóa từng đoạn mô hình phi tuyến dọc theo trục thời gian 
và giải pháp tối ưu hóa có ràng buộc để thiết kế bộ điều khiển. Trong giới hạn phạm 
vi nghiên cứu của luận án, tín hiệu điều khiển được thiết kế là lực (lực đẩy chân vịt) 
và mô-men (mô-men của bánh lái), chúng được ký hiệu là trong mô hình (2.40) 
và không quan tâm tới mô hình toán của cơ cấu thực hiện, như các công trình đã 
nghiên cứu về điều khiển tàu nổi có mô hình toán dạng thiếu cơ cấu chấp hành, 
không xét đến mô hình của cơ cấu chấp hành. 
2.3.1 Thiết kế bộ điều khiển dự báo phản hồi trạng thái điều khiển tàu chuyển 
 động bám quỹ đạo đặt khi mô hình tàu xác định 
 Ta thấy ngay rằng ở mô hình tàu thủy ba bậc tự do trong mặt phẳng ngang 
(2.40), trong trường hợp có thể xấp xỉ được: 
 gG()()   (2.42) 
với G() R33 là một ma trận phụ thuộc , thì nó sẽ là một hệ song tuyến. Vì vậy 
để đồng bộ với phần lý thuyết đã được trình bày ở trên, sau đây luận án sẽ viết lại 
mô hình toán tàu thủy ba bậc tự do trong mặt phẳng ngang (2.40) về dạng song 
tuyến chính tắc đã cho ở công thức (2.19) và (2.21) như sau: 
 Từ (2.40) và (2.42) có được: 
  033 J () 032 
  (2.43) 
  1 1
  GMCD()()()     MF
trong đó 033 là ma trận không kiểu 33 (3 hàng 3 cột). Do đó, khi đặt các biến 
mới x12 , x  , u  và x col( x12 , x ) , cũng như ký hiệu: 
 
 033 Jx()1 032 
 A( x ) , B , C I , 0 (2.44) 
 1 1 3 3 3 
 G()()() x1 M C x 2 D x 2  MF
với A( x ), B ( x ) là các ma trận có kiểu lần lượt là 66 và 62 , sẽ được: 
 49 
 x A() x x Bu
 (2.45) 
 y  I3 , 0 3 3 x Cx
trong đó I3 là ký hiệu của ma trận đơn vị kiểu . Như vậy, (2.45) là một hệ song 
tuyến và khi so sánh với hệ song tuyến nói chung, mô tả ở công thức tổng quát 
(2.19T), athì nó sẽ còn gần với hệ tuyến tính hơn ở chỗ là cả hai ma trận BC, của mô 
hình (2.45) đều là hằng số. Do đó, phương pháp điều khiển dự báo cho hệ song 
tuyến đã trình bày ở mục 2.1.3 là hoàn toàn áp dụng được để tín hiệu đầu ra y  
của mô hình tàu thủy ba bậc tự do trong mặt phẳng ngang dạng song tuyến (2.45) 
bám tiệm cận theo được quỹ đạo mẫu cho trước. 
 Để thiết kế bộ điều khiển dự báo phản hồi trạng thái cho mô hình (2.45) thì các 
biến trạng thái , trong đó xx12 , k giả thiết phải đo đạc hoặc 
xác định được trực tiếp. 
2.3.1.1 Mô hình dự báo trên cơ sở tuyến tính hóa từng đoạn mô hình dọc trục 
 thời gian 
 Do việc thiết kế bộ điều khiển dự báo cần tới mô hình không liên tục (mô hình 
rời rạc theo thời gian) nên ta sẽ rời rạc mô hình tàu thủy ba bậc tự do trong mặt 
phẳng ngang dạng liên tục (2.45) với một chu kỳ trích mẫu chọn trước. 
 Sử dụng công thức xấp xỉ: x( t ) x ( k 1) Ta x ( kT a ) T a và cho phép tính 
đạo hàm, thì mô hình liên tục (2.45) sẽ chuyển được về dạng rời rạc (2.46): 
 xk 1  I6 Taa A() x k x k T Bu k
 (2.46) 
 y Cxk
 wt() k xk
trong đó: x xkT( ), u ukT ( ), y ykT ( ) , I là ma trận đơn vị kiểu . 
 kka ak a 6
 33 
 Tiếp theo, ta xét tại thời điểm hiện tại. Nếu như tại đó véc-tơ trạng thái 
 x col( x12 , x )
là đã biết, có thể là do đo được trực tiếp từ hệ thống, hoặc do quan sát được từ 
những dữ liệu vào/ra đo được uy, , thì trong một khoảng thời gian đủ nhỏ, mô 
 k 1 k
hình song tuyến (2.46) ở trên sẽ xấp xỉ được bởi mô hình tuyến tính tham số hằng 
 k như (2.47): 66 
 50 
 zk 1 Ak z k B u k
 : (2.47) 
 k y Cz
 k k
trong đó: 
 82
 zk col x k , u k 11 RR , u k u k u k (2.48) 
 p
và 
 I6 Taa A() xka T B 8 8 TB 8 2 3 8
 ABCCk RRR, , , 032 (2.49) 
 02 6I 2 I2
 Từ mô hình xấp xỉ tuyến tính từng đoạn với k 0,1, cho ở (2.47), ta 
cũng có được công thức dự báo xấp xỉ cho tín hiệu đầu ra y, i  1,2, , N của 
 ki 
hệ (2.46) thuộc cửa sổ dự báo hiện tại [,)kN , như sau: 
 i i 12 i
 yk i CAz k k CABu k CABu k 11 CBu k i , 
trong đó N 2 là độ rộng cửa sổ dự báo được chọn trước. Viết chung các đầu ra 
tương lai đó lại với nhau theo cấu trúc véc-tơ cho toàn bộ cửa số dự báo, sẽ có: 
 y
 k CB 00 u CAk
 1 3 2 3 2 k 
 2
 y CAk B CB 032 u CA
 y k 2 k 1 k z
 k k (2.50) 
 y CANN 12 B CA B CB u N
 kN kk kN 1 CAk
 Hpk bk
với: 
 CB 00 u CAk
 3 2 3 2 k 
 2
 CAk B CB 032 u CA
 H k , p k 1 , b k z (2.51) 
 k kk 
 CANN 12 B CA B CB u N
 kk kN 1 CAk
trong đó là véc-tơ các tín hiệu đầu vào tương lai cần phải được xác định. 
2.3.1.2 Xây dựng khối hàm mục tiêu của bộ điều khiển MPC 
 Sau khi đã có được các tín hiệu đầu ra tương lai thuộc 
cửa sổ dự báo hiện tại dưới dạng các hàm số của tín hiệu đầu vào tương lai 
 51 
 ukj , j 0,1,  , N 1 cho ở công thức (2.50) thì để xác định được các đầu vào 
tương lai này sao cho đầu ra bám theo được dãy tín hiệu đặt {}wk . Ta cần một khối 
hàm mục tiêu thể hiện được mục đích bám tín hiệu đặt đó và một trong các hàm 
mục tiêu thể hiện được điều này là tổng bình phương các sai lệch bám thuộc của sổ 
dự báo hiện tại. p
 Tuy nhiên, nhằm nâng cao được tốc độ bám, ở đây luận án sẽ sử dụng kỹ thuật 
hiệu chỉnh tín hiệu đặt đã được nói tới ở mục 2.1.4.1 của chương 2, mà cụ thể là tín 
 rk
hiệu đặt sau hiệu chỉnh cho ở công thức (2.31) với: 
 wkk 1 Ke
 /
 r có wek w y() kT wa , (2.52) 
 k kkk
 wk N Ke k
trong đó là sai lệch bám dư thừa ở thời điểm trước đó và là 
tham số tùy chọn. 
 Hàm mục tiêu thể hiện được sai lệch bám nhỏ nhất giữa véc-tơ các tín hiệu 
đầu ra tương lai y cho ở công thức (2.50) và véc-tơ các tín hiệu đặt sau hiệu chỉnh 
 k
cho ở công thức (2.52) bây giờ sẽ là: 
 T T
 Jk( p ) y rkk Q k y r p R k p min . (2.53) 
 kk p
 3NNNN 3 2 2
trong đó QRkk RR, là hai ma trận đối xứng xác định dương tùy 
chọn. 
 Cuối cùng, nếu loại bỏ bớt những thành phần hằng số không phụ thuộc biến 
cần tìm trong hàm mục tiêu (2.53) ở trên, ta sẽ có hàm mục tiêu tương đương, 
nhưng với cấu trúc đơn giản hơn, như sau: 
 / T T T
 JppHQHRpk( ) k k k k 2 brkk QHp k k min . (2.54) 
 p
2.3.1.3 Xây dựng khối tối 01ƣu Khóa của bộ điều khiển 
 Nhiệm vụ của khối tối ưu hóa, như đã trình bày là xác định nghiệm của bài 
toán tối ưu: 
 52 
 /
 p* argmin Jk ( p ) (2.55) 
 pP 
có tập ràng buộc được suy ra từ điều kiện ràng buộc (2.41) về qui định giới hạn 
độ lớn góc bẻ lái tàu thủy. Giải pháp để tìm nghiệm của bài toán tối ưu có ràng buộc 
sử dụng kỹ thuật ước lượng xấp xỉ điều kiện ràng buộc thông qua thay đổi tham số 
 Ta
hàm mục tiêu, đã được trình bày tạip * mục 2.2.2 của chương 2. 
 Một cách cụ thể, nếu bài toán điều khiển không có ràng buộc, nghiệm của 
bài toán tối ưu (2.55) có hàm mục tiêu cho ở (2.54) sẽ là: 
 TT 1
 p* Hk Q k H k R k H k Q k brkk . (2.56) 
Khi đã có ta cũng có được tín hiệu điều khiển cho hệ điều khiển chuyển 
 k P
động tàu thủy (2.40) ở thời điểm hiện tại , suy ra từ công thức (2.48), như sau: 
 ukk u 1 I2, 0 2 2(N 1) p * (2.57) 
và nó sẽ được đưa vào để điều khiển trong phạm vi một khoảng thời gian trích mẫu 
 . 
 Nếu bài toán có điều kiện ràng buộc cho thì từ (2.57) ta thấy điều kiện ràng 
buộc đó đượcQRkk, chuyển sang điều kiện ràng buộc cho . Do điều kiện ràng buộc tín 
hiệu điều khiển với đối tượng tàu thủy trong luận án đều là các ràng buộc dạng 
 Q
khoảng cụ thể là gh u k   gh (suy ra từ ràng buộc độk lớn góc bẻ lái), nên ta 
có thể thay đổi để thỏa mãn Rcáck điều kiện ràng buộc này. Chi tiết hơn, 
cônguk thức (2.56) cho thấy nếu càng lớn sẽ càng nhỏ, ngược lại càng lớn 
 sẽ càng lớn. 
2.3.1.4 Thuật toán bộ điều khiển dự báo phản hồi trạng thái 
 Hình 2.5 biểu diễn thuật toán các bước tính cần thực hiện trong một vòng lặp ở 
thời điểm hiện tại để xác định được tín hiệu điều khiển và minh họa cấu trúc 
trượt dọc trên trục thời gian của bộ điều khiển. 
 53 
 Bắt đầu
 Tùy chọn:
 Cửa sổ dự báo N 2, thời gian trích mẫu Ta
 Hệ số hiệu chỉnh và giá trị ràng buộc  1, ugh
 Hệ số hiệu chỉnh tín hiệu đặt 01 K
 Tính BC, theo (2.44) và BC, theo (2.49)
 Gán: Ma trận xác định dương QQRR TT 0, 0,
 Giá trị khởi tạo k 0, u 1 0, e 0 0, A0  , x 0 
 Đo: Trạng thái xk col(,) từ đối tượng điều khiển (2.40)
 Tính:
 Ak theo (2.49). Và Hk ,,brkktheo (2.51), (2.52)
 Tìm: 
 p * theo (2.56), sau đó tính u theo (2.57)
 Gán: Nghiệm tối ưu k
 kk:1 
 xx0 
 uu Ràng buộc 
 0 sai
 AA0 tín hiệu điều 
 khiển = 1 
 ?
 Gán:
 RR . đúng
 sai
 uuk gh ?
 đúng
uk
 Đƣa: vào điều khiển đối tượng liên tục (2.40), hay (2.45)
 sai Lệnh dừng 
 điều khiển =1
 ?
 đúng
 Kết thúc
 a. Thuật toán xác định tín hiệu điều khiển bộ điều khiển MPC-S 
 54 
 Ta
 kT
 a kTa  (kT 1) a t
 Tính uk 1
 uk
 Ta Thuật toán xác định tín 
 hiệu điều khiển uk
 b. Minh họa thuật toán bộ điều khiển MPC-S trượt dọc trên trục thời gian 
 Hình 2.5 Thuật toán điều khiển dự báo phản hồi trạng thái (MPC-S), điều khiển 
 chuyển động tàu thủy bám quỹ đạo đặt. 
 Khoảng thời gian chênh lệch giữa khi đo được trạng thái và có được 
là khoảng thời gian cần thiết để thực hiện tất cả các phép tính, bao gồm xác định 
 Akk,,,, Hbrkk p * và cuối cùng là . Về nguyên tắc, với tốc độ tính toán hiện nay 
của các thiết bị số thì là rất nhỏ và có thể bỏ qua được. 
 Khi đã có , nó sẽ được đưa vào điều khiển hệ (2.40), và cũng là hệ liên tục 
(2.45), trong đúng một khoảng thời gian trích mẫu , từ thời điểm kTa  tới thời 
 uk 1 
điểm (k 1)Ta  . Ở thời điểm (kT 1) a vòng tính toán lặp trên được thực hiện lại, 
bắt đầu bằng việc đo trạng thái xk 1, tính toán Akk 11,,,, Hbrkk 11 p * để rồi lại 
có cho chu kỳ trích mẫu tiếp theo. 
 uk Như vậy, hệ điều khiển vòng kín, bao gồm đối tượng điều khiển là hệ liên tục 
 x
(2.40) và bộ điều khiểnk số (bộ điều khiển dự báo) sẽ là một hệ sampled data. 
 Thuật toán điều khiển dự báo phản hồi trạng thái được luận án ký hiệu là 
MPC-S, trong đó ký tự S được thêm vào để ngụ ý rằng đây là thuật toán điều khiển 
phản hồi trạng thái (system states). 
2.3.1.5 Mô phỏng bộ điều khiển MPC-S 
 a. Đối tƣợng và quỹ đạo mô phỏng 
 Đối tượng nghiên cứu thiết kế điều khiển là tàu thủy với mô hình ba bậc tự do 
trên mặt phẳng ngang có mô hình toán dạng thiếu cơ cấu chấp hành, thông số kỹ 
 55 
thuật của tàu sử dụng mô phỏng được lấy từ tài liệu [21] của tác giả Do K. D and J. 
Pan (2009). Số liệu chi tiết thông số tàu, tham số của mô hình toán được cho trong 
bảng PL.1 phụ lục 2. Số liệu thông số tàu này đã được nhiều tác giả sử dụng để mô 
phỏng, kiểm chứng bộ điều khiển khi nghiên cứu về mô hình tàu thiếu cơ cấu chấp 
hành như các công trình: [14], [16] - [21], [48] và [64]). 
 Để kiểm tra chất lượng bám quỹ đạo của bộ điều khiển đề xuất, luận án đưa ra 
hai quỹ đạo đặt thường hay áp dụng với tàu biển trong quá trình chạy kiểm tra đặc 
tính điều động và quay trở tàu như sau: 
 Quỹ đạo 1: tàu chạy theo quỹ đạo đường thẳng, sau đó tàu chạy lượn vòng tròn 
với bán kính lượn vòng 200(m), luận án gọi là quỹ đạo hình tròn, Hình 2.6a. 
 Quỹ đạo 2: tàu chạy theo đường thẳng, sau đó chạy quỹ đạo zíc-zắc hình sin 
với biên độ 175m, sau đó chạy tiếp với quỹ đạo thẳng, luận án gọi là quỹ đạo hình 
sin, Hình 2.6b. 
 a) Quỹ đạo đặt hình tròn với bán kính 200(m) 
 b) Quỹ đạo đặt hình sin với biên độ hình sin 175(m) 
 Hình 2.6 Quỹ đạo đặt kiểm chứng chất lượng bộ điều khiển. 
 Ký hiệu các đại lượng trong mô phỏng như sau: 
  [,,]xy – lần lượt là quỹ đạo vị trí và hướng đi đặt của tàu. 
 d d d d
 56 
 ex x d x,, e y y d y e hd  d – lần lượt là sai lệch bám quỹ đạo theo 
trục , và sai lệch bám hướng đi. 
 Thời gian mô phỏng được tính bằng giây [s], tọa độ quỹ đạo trên mặt phẳng 
ngang của tàu trong hệ trục tọa độ trái đất theo đơn vị dài là [m], hướng đi của 
tàu theo đơn vị là độ [deg], trong đó hướng 0 độ trùng với hướng Bắc thật của Trái 
Đất. Đơn vị lực tác động là [N], mô-men [N.m], vận tốc dài [m/s], và vận tốc góc 
[rad/s]. 
 b. Kết quả mô phỏng 
 Chương trình bộ điều khiển viết theo thuật toán điều khiển MPC-S, với các 
tham số cài đặt như sau: 
 Cửa sổ dự báo: (cài đặt N 5) 
 Thời gian trượt (receding horizon) Tsa 0.1( ) 
 Tham số hiệu chỉnh tín hiệu đặt (cài đặt K 0.2) 
 N 2
 Tín hiệu điều khiển ban đầu ở thời điểm t 1 (u 1 0 ) 
 Ma trận xác định dương QR, (đặt Q diag([50;50;100]); R diag ([1;1]) ) 
 Cài đặt ràng buộc tín hiệu điều khiển (giả thiết giá trị ràng buộc được đặt là 
 5
 r. gh 8.10 (Nm . )) và tín hiệu điều khiển mô-men quay trở phải thỏa mãn: 
 Giá trị banx đầu của quỹ đạo đặt và quỹ đạo vị trí tàu: 
 y
 Quỹ đạo hình tròn: xyd(0) 0, d (0) 50, d (0) 0, 
 x(0) 0, y (0) 30, (0) 0, u (0) 4, v (0) 2.3, r (0) 0.1 
 xoy
 Quỹ đạo hình sin: xyd(0) 5, d (0) 30, d (0) 0 
 x(0) 0, y (0) 20, (0) 0, u (0) 4, v (0) 2.3, r (0) 0.1 
 Sơ đồ mô phỏng bộ điều khiển MPC-S được đưa ra trong phần phụ lục 3 của 
luận án. 
 01 K
 r.. gh  r  r gh
 57 
Kết quả mô phỏng bộ điều khiển MPC-S với quỹ đạo hình tròn 
 a) Kết quả mô phỏng quỹ đạo chuyển động – quỹ đạo hình tròn (MPC-S) 
 b) Sai lệch bám quỹ đạo – quỹ đạo hình tròn (MPC-S) 
 u
 c) Sai lệch bám hướng đi – quỹ đạo hình tròn (MPC-S) 
 d) Tín hiệu điều khiển lực trượt dọc – quỹ đạo hình tròn (MPC-S) 
 58 
 e) Tín hiệu điều khiển mô-men quay trở khi không ràng buộc – quỹ đạo hình 
 tròn (MPC-S) 
 f) Tín hiệu điều khiển mô-men quay trở , khi có ràng buộc với giả thiết giá trị 
 55
 ràng buộc là 8.10 (N . m ) r 8.10 ( N . m ) – quỹ đạo hình tròn (MPC-S) 
 Hình 2.7 Kết quả mô phỏng, kiểm chứng chất lượng bộ điều khiển MPC-S với quỹ 
 đạo hình tròn 
Kết quả mô phỏngr bộ điều khiển MPC-S với quỹ đạo hình sin 
 a) Kết quả mô phỏng quỹ đạo chuyển động – quỹ đạo hình sin (MPC-S) 
 59 
 b) Sai lệch bám quỹ đạo – quỹ đạo hình sin (MPC-S) 
 c) Sai lệch bám hướng đi – quỹ đạo hình sin (MPC-S) 
 u
 r 
 d) Tín hiệu điều khiển lực trượt dọc – quỹ đạo hình sin (MPC-S) 
e) Tín hiệu điều khiển mô-men , không ràng buộc – quỹ đạo hình sin (MPC-S) 
 60 
 f) Tín hiệu điều khiển mô-men quay trở , khi có ràng buộc với giả thiết giá trị 
 ràng buộc là – quỹ đạo hình sin (MPC-S) 
 Hình 2.8 Kết quả mô phỏng, kiểm chứng chất lượng bộ điều khiển MPC–S với quỹ 
 đạo hình sin 
 Nhận xét: 
 Kết quả mô phỏng bộ điều khiển MPC-S cho thấy khi thử nghiệm với hai quỹ 
đạo đặt là quỹ đạo hình tròn, quỹ đạo hình sin cho tín hiệu quỹ đạo đầu bám theo 
quỹ đạo đặt với chất lượng tốt khi tín hiệu điều khiển u2 r có ràng buộc (ràng 
buộc về giá trị mô-men tương đương với điều kiện ràng buộc về góc bẻ lái). 
 Sai lệch bám quỹ đạo55 eexy, , sai lệch bám hướng có giá trị nhỏ so với quỹ 
 8.10 (N . m ) r 8.10 (