Luận án Nghiên cứu nâng cao hiệu năng bám mã cho DLL sử dụng cấu trúc đa tương quan như cải tiến cấu trúc DDC và tối ưu cấu trúc MGD

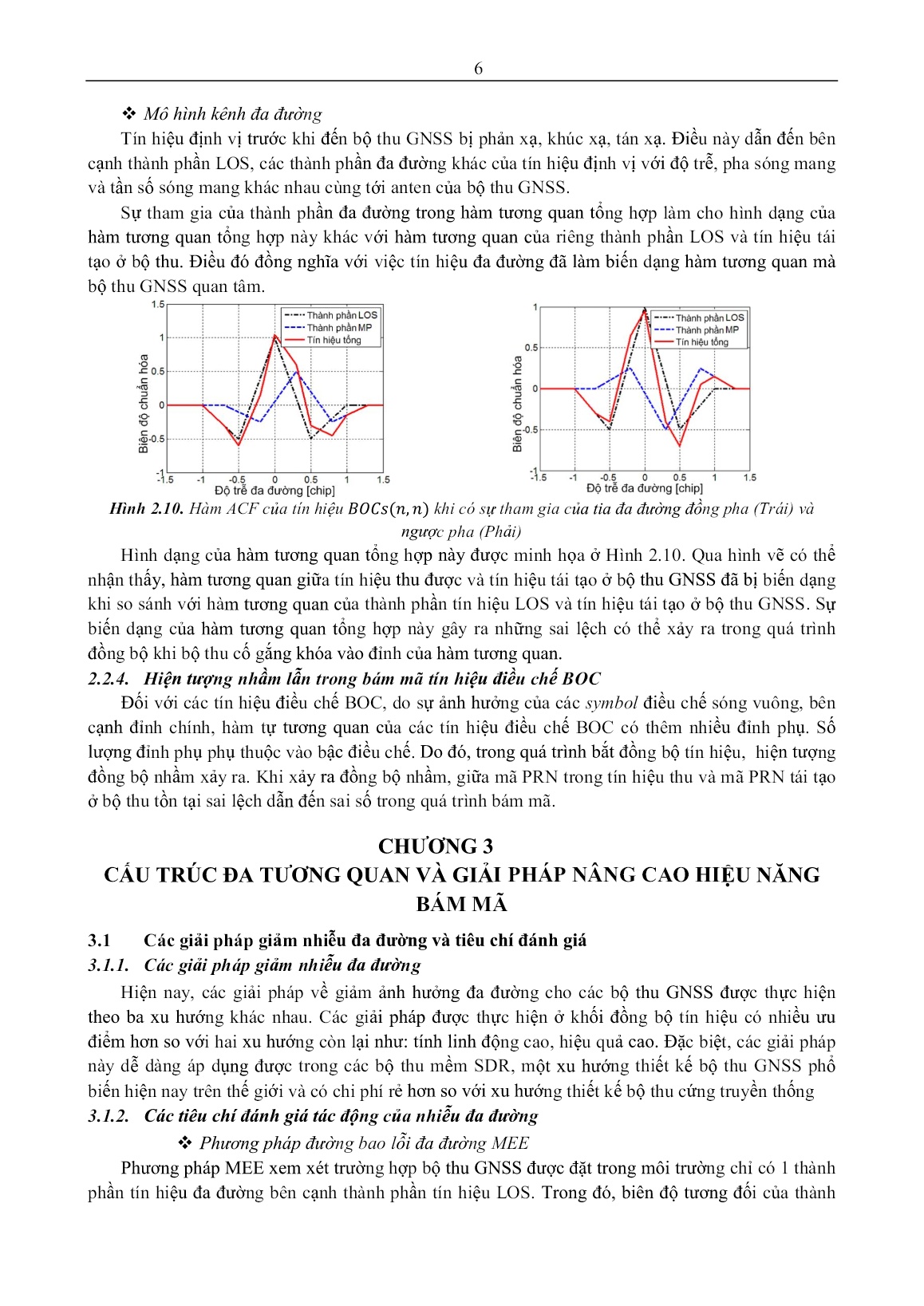
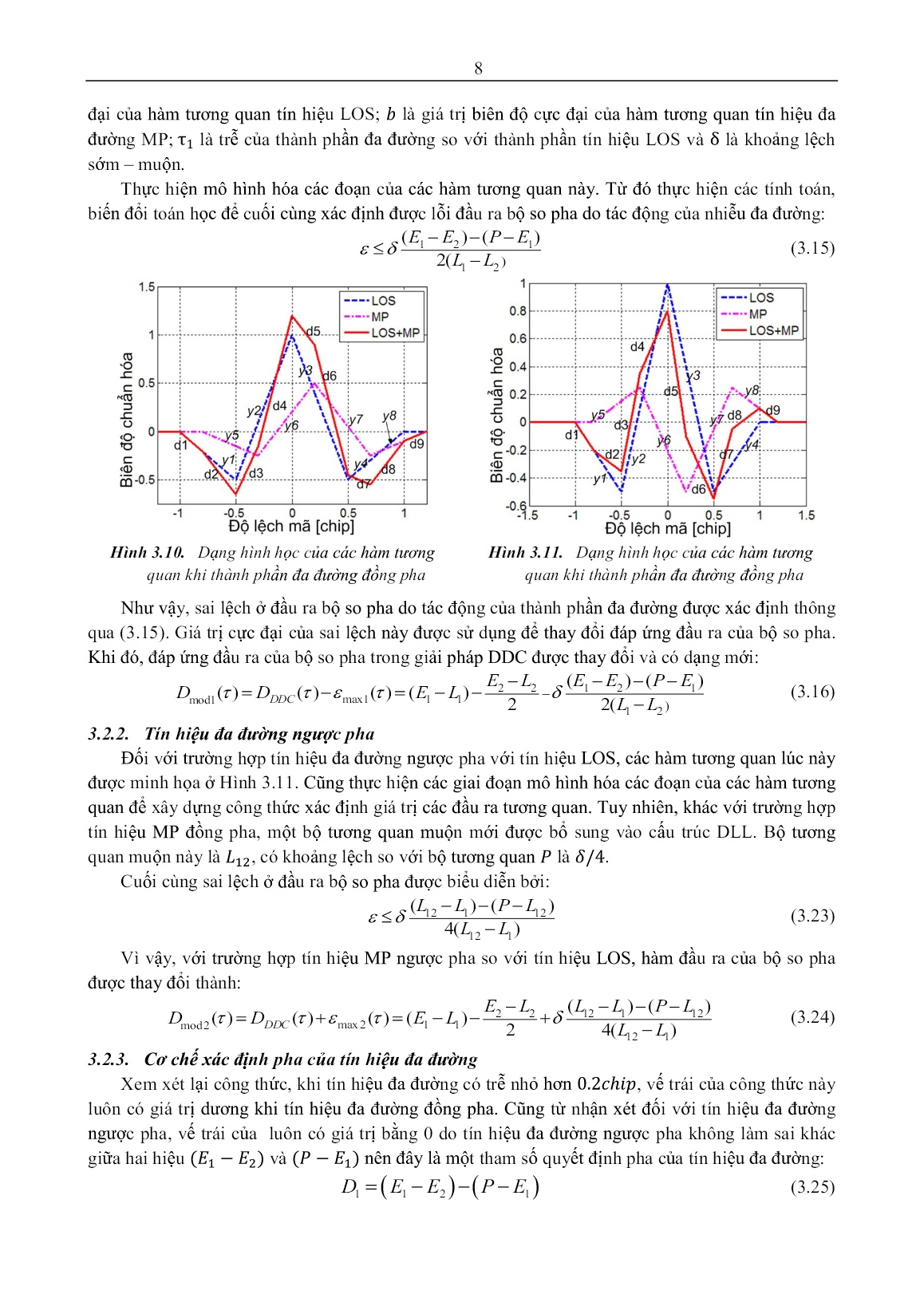
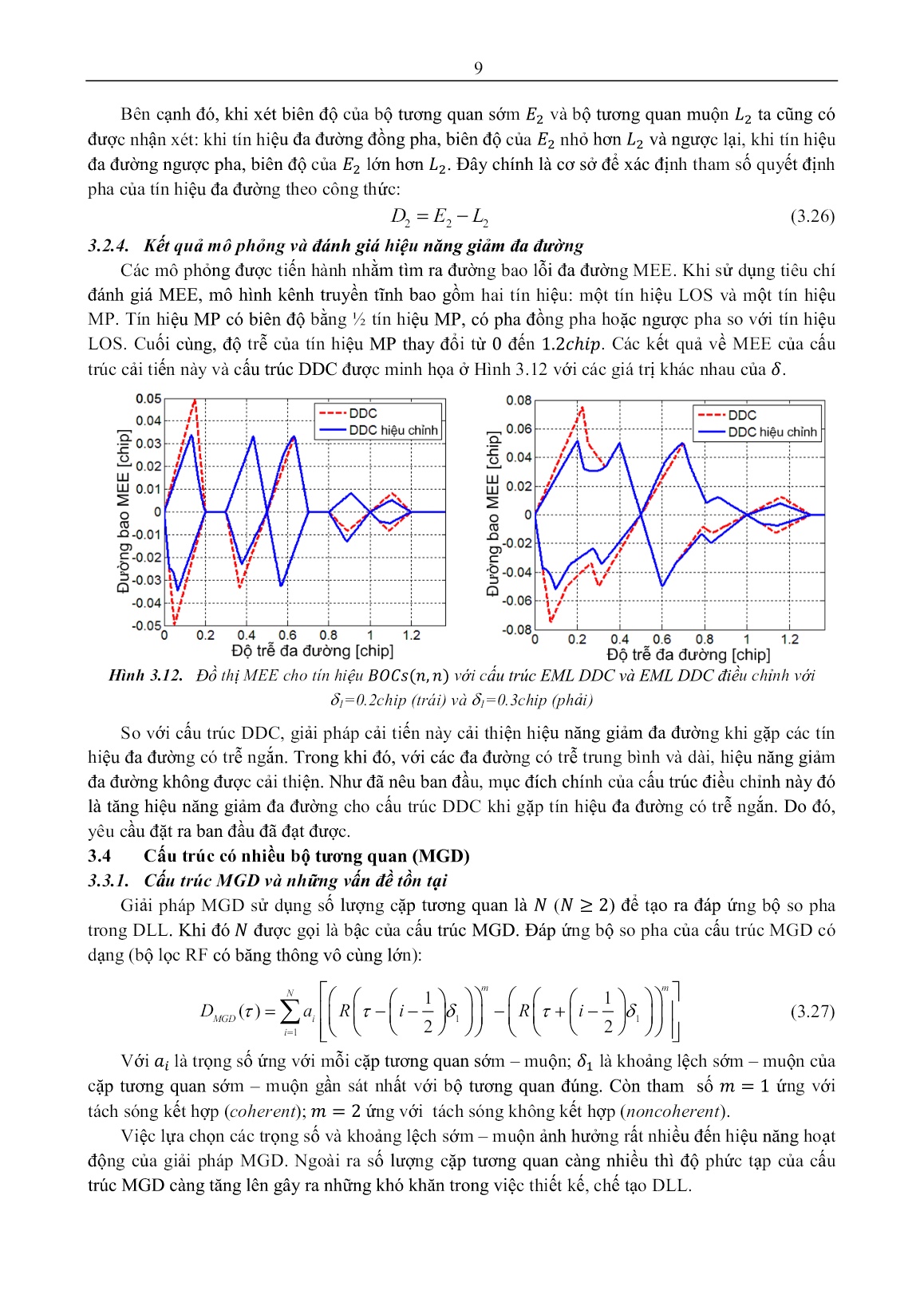
í rẻ hơn so với xu hướng thiết kế bộ thu cứng truyền thống 
3.1.2. Các tiêu chí đánh giá tác động của nhiễu đa đường 
  Phương pháp đường bao lỗi đa đường MEE 
 Phương pháp MEE xem xét trường hợp bộ thu GNSS được đặt trong môi trường chỉ có 1 thành 
phần tín hiệu đa đường bên cạnh thành phần tín hiệu LOS. Trong đó, biên độ tương đối của thành 
 7 
phần đa đường so với thành phần LOS duy trì không đổi trong suốt quá trình đánh giá tác động của 
hiện tượng đa đường. Việc tính toán đường bao lỗi trung bình tương đương với việc tìm ra điểm cắt 
0 của đáp ứng bộ so pha vì đây là điểm khóa ổn định của mạch vòng DLL. 
  Phương pháp đường bao lỗi trung bình RAE 
 Để đánh giá thực tế hơn, phương pháp giá trị trung bình của MEE (RAE) được sử dụng để thay 
thế cho MEE. Trong phương pháp RAE, chỉ những giá trị tuyệt đối của đường bao mới được xem 
xét và tổng tích lũy của chúng được sử dụng để tính lỗi trung bình. 
3.2 Cấu trúc bộ tƣơng quan kép (DDC) 
 Trong giải pháp DDC, thay vì chỉ sử dụng 03 bộ tương quan như trong NC , DLL sử dụng 05 
bộ tương quan (hai bộ tương quan Sớm ; hai bộ tương quan Muộn và một bộ tương 
quan Đúng . Các bộ tương quan này cách đều nhau về mặt độ trễ. Trong trường hợp tách sóng 
kết hợp (coherent), đáp ứng bộ so pha trong DLL của khối bám tín hiệu là sự kết hợp tuyến tính 
giữa các đầu ra tương quan theo công thức: 
 1
 DELEL()()()()()     (3.5) 
 DDC 1 12 2 2
 Hình 3.5. Cấu trúc DLL dạng DDC hoạt động với tín hiệu . 
 Với cách điều chỉnh cấu trúc của khối bám mã như vậy, giải pháp DDC có hiệu năng giảm 
nhiễu đa đường tốt hơn khá nhiều so với giải pháp NC, đặc biệt với những trễ đa đường trong 
khoảng từ trung bình đến dài (tín hiệu đa đường có trễ tương đối so với tín hiệu LOS từ đến 
 ). Tuy nhiên, với những trễ đa đường gần (độ lệch giữa thành phần đa đường và thành phần 
LOS nhỏ hơn , giải pháp DDC vẫn không có sự vượt trội so với giải pháp NC. 
 Vì vậy, để có thể cải thiện được hiệu năng giảm ảnh hưởng đa đường của giải pháp DDC, sai số 
của giải pháp DDC do ảnh hưởng của đa đường được đánh giá. Trên cơ sở xác định được sai số đó, 
ta tiến hành bù lại phần sai lệch đó để khắc phục sai lệch do đa đường gây ra. Khi có sự tham gia 
của thành phần đa đường, đỉnh tương quan này bị lệch ra khỏi điểm lệch 0. Tùy thuộc vào pha 
của thành phần đa đường, đỉnh tương quan này có thể bị lệch sang phải hoặc sang trái điểm lệch 
0. Điều này tương đương với điểm khóa của bộ so pha DLL bị dịch sang bên phải hoặc sang bên 
trái của điểm lệch 0. 
3.3 Điều chỉnh đáp ứng bộ so pha của cấu trúc DDC 
3.2.1. Tín hiệu đa đường đồng pha 
 Trường hợp tín hiệu đa đường đồng pha với tín hiệu, các hàm tương quan của tín hiệu tạo ra ở 
bộ thu với các tín hiệu LOS (LOS ACF), tín hiệu đa đường (MP) (MP ACF) và tín hiệu tổng được 
minh họa ở Hình 3.10. 
 Gọi  là lỗi đầu ra của bộ so pha do ảnh hưởng của đa đường (lỗi này tương ứng với độ lệch 
của đầu ra bộ tương quan đúng khỏi điểm lệch 0 (điểm tương quan đúng); là giá trị biên độ cực 
 8 
đại của hàm tương quan tín hiệu LOS; là giá trị biên độ cực đại của hàm tương quan tín hiệu đa 
đường MP; là trễ của thành phần đa đường so với thành phần tín hiệu LOS và là khoảng lệch 
sớm – muộn. 
 Thực hiện mô hình hóa các đoạn của các hàm tương quan này. Từ đó thực hiện các tính toán, 
biến đổi toán học để cuối cùng xác định được lỗi đầu ra bộ so pha do tác động của nhiễu đa đường: 
 ()()EEPE 
  1 2 1 (3.15) 
 2(LL12 )
 Hình 3.10. Dạng hình học của các hàm tương Hình 3.11. Dạng hình học của các hàm tương 
 quan khi thành phần đa đường đồng pha quan khi thành phần đa đường đồng pha 
 Như vậy, sai lệch ở đầu ra bộ so pha do tác động của thành phần đa đường được xác định thông 
qua (3.15). Giá trị cực đại của sai lệch này được sử dụng để thay đổi đáp ứng đầu ra của bộ so pha. 
Khi đó, đáp ứng đầu ra của bộ so pha trong giải pháp DDC được thay đổi và có dạng mới: 
 ELEEPE2 2()() 1 2 1
 DDELmod1()()()() DDC  max1  1 1  (3.16) 
 2 2(LL12 )
3.2.2. Tín hiệu đa đường ngược pha 
 Đối với trường hợp tín hiệu đa đường ngược pha với tín hiệu LOS, các hàm tương quan lúc này 
được minh họa ở Hình 3.11. Cũng thực hiện các giai đoạn mô hình hóa các đoạn của các hàm tương 
quan để xây dựng công thức xác định giá trị các đầu ra tương quan. Tuy nhiên, khác với trường hợp 
tín hiệu MP đồng pha, một bộ tương quan muộn mới được bổ sung vào cấu trúc DLL. Bộ tương 
quan muộn này là , có khoảng lệch so với bộ tương quan là . 
 Cuối cùng sai lệch ở đầu ra bộ so pha được biểu diễn bởi: 
 ()()LLPL 
  12 1 12 (3.23) 
 4(LL12 1 )
 Vì vậy, với trường hợp tín hiệu MP ngược pha so với tín hiệu LOS, hàm đầu ra của bộ so pha 
được thay đổi thành: 
 ELLLPL2 2()() 12 1 12
 DDELmod2()()()() DDC  max2  1 1  (3.24) 
 2 4(LL12 1 )
3.2.3. Cơ chế xác định pha của tín hiệu đa đường 
 Xem xét lại công thức, khi tín hiệu đa đường có trễ nhỏ hơn , vế trái của công thức này 
luôn có giá trị dương khi tín hiệu đa đường đồng pha. Cũng từ nhận xét đối với tín hiệu đa đường 
ngược pha, vế trái của luôn có giá trị bằng 0 do tín hiệu đa đường ngược pha không làm sai khác 
giữa hai hiệu và nên đây là một tham số quyết định pha của tín hiệu đa đường: 
 DEEPE1 1 2 1 (3.25) 
 9 
 Bên cạnh đó, khi xét biên độ của bộ tương quan sớm và bộ tương quan muộn ta cũng có 
được nhận xét: khi tín hiệu đa đường đồng pha, biên độ của nhỏ hơn và ngược lại, khi tín hiệu 
đa đường ngược pha, biên độ của lớn hơn . Đây chính là cơ sở để xác định tham số quyết định 
pha của tín hiệu đa đường theo công thức: 
 DEL2 2 2 (3.26) 
3.2.4. Kết quả mô phỏng và đánh giá hiệu năng giảm đa đường 
 Các mô phỏng được tiến hành nhằm tìm ra đường bao lỗi đa đường MEE. Khi sử dụng tiêu chí 
đánh giá MEE, mô hình kênh truyền tĩnh bao gồm hai tín hiệu: một tín hiệu LOS và một tín hiệu 
MP. Tín hiệu MP có biên độ bằng ½ tín hiệu MP, có pha đồng pha hoặc ngược pha so với tín hiệu 
LOS. Cuối cùng, độ trễ của tín hiệu MP thay đổi từ đến . Các kết quả về MEE của cấu 
trúc cải tiến này và cấu trúc DDC được minh họa ở Hình 3.12 với các giá trị khác nhau của . 
 Hình 3.12. Đồ thị MEE cho tín hiệu với cấu trúc EML DDC và EML DDC điều chỉnh với 
 1=0.2chip (trái) và 1=0.3chip (phải) 
 So với cấu trúc DDC, giải pháp cải tiến này cải thiện hiệu năng giảm đa đường khi gặp các tín 
hiệu đa đường có trễ ngắn. Trong khi đó, với các đa đường có trễ trung bình và dài, hiệu năng giảm 
đa đường không được cải thiện. Như đã nêu ban đầu, mục đích chính của cấu trúc điều chỉnh này đó 
là tăng hiệu năng giảm đa đường cho cấu trúc DDC khi gặp tín hiệu đa đường có trễ ngắn. Do đó, 
yêu cầu đặt ra ban đầu đã đạt được. 
3.4 Cấu trúc có nhiều bộ tƣơng quan (MGD) 
3.3.1. Cấu trúc MGD và những vấn đề tồn tại 
 Giải pháp MGD sử dụng số lượng cặp tương quan là ( ) để tạo ra đáp ứng bộ so pha 
trong DLL. Khi đó được gọi là bậc của cấu trúc MGD. Đáp ứng bộ so pha của cấu trúc MGD có 
dạng (bộ lọc RF có băng thông vô cùng lớn): 
 mm
 N 11 
 DMGD()  a i R  i 11 R  i  (3.27) 
 i 1 22 
 Với là trọng số ứng với mỗi cặp tương quan sớm – muộn; là khoảng lệch sớm – muộn của 
cặp tương quan sớm – muộn gần sát nhất với bộ tương quan đúng. Còn tham số ứng với 
tách sóng kết hợp (coherent); ứng với tách sóng không kết hợp (noncoherent). 
 Việc lựa chọn các trọng số và khoảng lệch sớm – muộn ảnh hưởng rất nhiều đến hiệu năng hoạt 
động của giải pháp MGD. Ngoài ra số lượng cặp tương quan càng nhiều thì độ phức tạp của cấu 
trúc MGD càng tăng lên gây ra những khó khăn trong việc thiết kế, chế tạo DLL. 
 10 
3.3.2. Cấu trúc MGD với 7 bộ tương quan 
3.3.2.1. Đề xuất cấu trúc 
 Trên cơ sở những phân tích ở trên, cấu trúc MGD được đề xuất gồm 3 tầng ứng với 3 cặp tương 
quan sớm muộn như Hình 3.13. Đồng thời, một cấu trúc DLL dựa trên cấu trúc đó được đề xuất áp 
dụng. Trong cấu trúc này, khoảng lệch của các cặp tương quan sớm – muộn , tương ứng 
các bộ tương quan Sớm, Muộn cách đều nhau. Hàm đầu ra của bộ so pha ở dạng “noncoherent” 
được biểu diễn: 
 3 22
 (3.31) 
 Dp MGD ( )  ai R   i / 2 R   i / 2 
 i 1 
 NCO Lọc vòng
 2 -
 () 
 +
 () 2 a1
 Tạo sóng 
 mang NCO () 2
 Các bản sao Muộn
 
 ()
 B
 ộ
 L3 L2 L1 
 - s
 st() p MGD
 o
 Bộ tạo sóng D
 Bộ tạo mã 
 mang con p
 E3 E2 E1 + h
 a2 a
 Các bản sao Sớm
 -
 2 +
 () 
 () 2 a3
 () 2
 NCO: Bộ tạo dao động điều khiển số 
 Hình 3.13. Sơ đồ khối cấu trúc MGD đề xuất 
 Việc lựa chọn các hệ số ảnh hưởng rất nhiều đến hiệu năng hoạt động của khối bám 
mã khi xét đến nhiễu đa đường. Bên cạnh đó, việc lựa chọn các hệ số này ảnh hưởng đến đặc tính 
đầu ra của bộ so pha. Tiêu chí để đánh giá đặc tính đầu ra bộ so pha đó chính là hàm đầu ra bộ so 
pha chỉ có một điểm cắt 0 là điểm cắt 0 đúng ứng với độ lệch bằng 0 giữa mã PRN trong tín hiệu 
định vị thu được và mã PRN tạo ra ở bộ thu. 
3.3.2.2. Tối ưu các hệ số trong cấu trúc MGD 
  Nâng cao độ chính xác – tránh bám nhầm với tín hiệu 
 Giai đoạn thứ nhất của quá trình tối ưu nhằm tìm ra các cặp hệ số để hàm đầu ra của 
bộ so pha không còn các điểm khóa nhầm. Do vậy, đáp ứng đầu ra của bộ so pha phải thỏa mãn 
điều kiện sau: 
 Dp MGD ( ) 0, 0 1( chip )
 (3.33) 
 Dp MGD ( ) 0, -1 0( chip )
 Biểu thức (3.33) đồng nghĩa với vùng làm việc ổn định của bộ so pha trải rộng thành . 
 Các hàm đầu ra bộ so pha dạng NC – EMLP hầu hết đều tồn tại hai điểm khóa phụ bên cạnh 
một điểm khóa chính khi thực hiện với tín hiệu định vị . Với cấu trúc MGD được đề 
xuất ở đây có số cặp tương quan sớm – muộn và khoảng lệch sớm – muộn tuân theo quy 
luật thì điều kiện để có thể tối ưu được các hệ số là . 
 Thực hiện điều chỉnh các hệ số của cấu trúc MGD với khoảng giá trị (việc lựa chọn 
khoảng giá trị này tương ứng với việc chuẩn hóa theo giá trị của hệ số với và 
cũng không mất đi tính tổng quát của bài toán) và bước dịch của các hệ số là , các bộ hệ số 
 nhận được khá nhiều ứng với mỗi giá trị của khoảng lệch sớm – muộn . 
 11 
 Hình 3.17. Đáp ứng bộ so pha của cấu trúc EMLP NC, EMLP DDC, và MGD có 
 (trái) và 
 Hình 3.17 minh họa đáp ứng bộ so pha của cấu trúc MGD được tối ưu ở giai đoạn này với các 
cặp hệ số được xác định ứng với các giá trị khác nhau của khoảng lệch sớm – muộn và bỏ qua ảnh 
hưởng của bộ lọc RF. Quan sát các hình vẽ, ta nhận thấy thông qua việc lựa chọn các hệ số theo tiêu 
chí tối ưu được đưa ra ban đầu, các đáp ứng của bộ so pha của cấu trúc MGD không xuất hiện các 
điểm khoa nhầm. Bộ so pha chỉ có một điểm cắt 0 trong khoảng , điều này cho phép 
mạch vòng bám mã tránh được hiện tượng bám nhầm. 
  Tối ưu hiệu năng giảm ảnh hưởng đa đường 
 Hình 3.20. Miền bao phủ của lỗi bám mã với cấu trúc MGD 
 Sang đến giai đoạn thứ hai, ứng với mỗi khoảng lệch sớm – muộn cần phải tìm ra ít nhất một 
bộ hệ số mà giúp cho cấu trúc MGD có khả năng giảm ảnh hưởng đa đường tốt nhất. Trong 
trường hợp này, khả năng giảm đa đường của mạch vòng DLL sử dụng cấu trúc MGD là tối ưu nếu 
lỗi trung bình nhỏ, sai số cực đại nhỏ và giá trị cực đại của trễ đa đường mà sau đó giá trị của MEE 
tiến về 0 cũng có giá trị nhỏ. Để thuận tiện khi đánh giá, các tiêu chí này được kết hợp lại thành tiêu 
chí miền bao phủ (enclosed area). 
 Hình 3.20 minh họa miền bao phủ của cấu trúc MGD với các tham số của mạch vòng DLL 
được cho ở hình vẽ. Các điều kiện ban đầu như: không có nhiễu AWGN, chiều dài mã PRN đủ lớn, 
không có sai pha sóng mang và bỏ qua ảnh hưởng của bộ lọc RF. Đồng thời, tín hiệu đa đường có 
biên độ tương đối là , trễ của thành phần đa đường biến đổi từ 0 đến (với bước dịch của 
độ trễ là ). Căn cứ vào những tiêu chí vừa nêu và các điều kiện đầu của bài toán, khảo sát 
với các cặp hệ số khác nhau của đã xác định ở phần trước để tìm ra một số cặp hệ số tối ưu 
cho hiệu năng giảm đa đường. 
 12 
 Thực hiện tính toán với các giá trị khác nhau của để tìm ra được các cặp hệ số tối 
ưu về hiệu quả giảm đa đường cho cấu trúc MGD. Các kết quả này được mô tả ở Bảng 3.6. 
 Bảng 3.6. Giá trị tối ưu các hệ số của cấu trúc MGD 
 Khoảng lệch sớm – Miền bao phủ Miền bao phủ Miền bao phủ của 
 a a 
 muộn [chip] 2 3 của MGD của NC DDC 
 4.8797 5.3981 3.8088 
 1 0.2 -0.5 0.6 
 6.0894 7.0228 6.1869 
 1 0.25 -0.5 0.4 
 8.4809 7.7959 8.0334 
 1 0.3 -0.4 1 
  0.35 -0.2 0.7 8.8069 9.0969 9.3691 
 1 
 10.2872 9.8987 9.9934 
 1 0.4 -0.1 0.8 
  0.45 0 0.3 10.3466 9.7313 10.0231 
 1 
 So sánh các kết quả về miền bao phủ của các cấu trúc MGD, DDC và NC với các khoảng lệch 
sớm – muộn khác nhau, ta nhận thấy, cấu trúc MGD có hiệu quả giảm đa đường tốt hơn NC nhưng 
có thể vẫn kém hơn so với DDC. Tuy nhiên, sự sai khác này là không quá lớn. Hiệu năng của cấu 
trúc MGD có được phải trả giá bằng cấu trúc mạch vòng DLL phức tạp hơn và khối lượng tính toán 
của bộ so pha cũng nhiều hơn. Bù lại sự suy giảm đó, cấu trúc MGD đề xuất còn có được lợi thế về 
việc tránh bám nhầm vào các đỉnh phụ của hàm ACF. Hiệu năng về giảm đa đường của cấu trúc 
MGD với cặp hệ số tối ưu được so sánh với các cấu trúc DDC, NC được minh họa ở Hình 3.21 với 
các giá trị khác nhau của khoảng lệch sớm – muộn. 
 Hình 3.21. MEE của cấu trúc EMLP NC, EMLP DDC, và MGD có 
 (trái) và (phải). 
 CHƢƠNG 4 
 CẢI THIỆN HIỆU NĂNG BÁM MÃ VỚI TÍN HIỆU ĐIỀU CHẾ BOC CHO 
 MẠCH VÒNG KHÓA TRỄ 
4.1. Các giải pháp bám mã chính xác cho tín hiệu BOC 
 Hiện tượng bám nhầm cũng gây ra những sai số trong quá trình bám mã do ở trạng thái khóa 
của DLL vẫn tồn tại sai lệch giữa mã PRN trong tín hiệu định vị thu được và mã PRN được tạo ra ở 
bộ thu GNSS. Vì vậy, đã có nhiều giải pháp nhằm loại bỏ các đỉnh phụ trong hàm ACF để tránh 
nguy cơ đồng bộ nhầm như: kỹ thuật “Bump- Jump”, giải pháp “BPSK-like”, giải pháp khử đỉnh 
phụ với tên gọi triệt pha sóng mang con (SCPC) và tạo ra một hàm tương quan mới có dạng giống 
với hàm ACF của tín hiệu BPSK. Ngoài ra còn có các giải pháp dựa trên hàm tương quan BOC – 
PRN cũng đã được đề xuất. Tuy nhiên, với mỗi giải pháp đều tồn tại một số nhược điểm như: không 
 13 
duy trì được những ưu điểm về búp chính hẹp phương thức điều chế BOC; có hiệu năng giảm đa 
đường không tốt hoặc chỉ áp dụng được với một dạng điều chế BOC; các đỉnh phụ vẫn còn tồn tại 
với biên độ khá lớn. 
 Vì vậy, việc nghiên cứu đề xuất giải pháp loại bỏ các đỉnh phụ của hàm ACF để tránh xảy ra 
hiện tượng bám nhầm, đồng thời vẫn duy trì được các ưu điểm của dạng điều chế BOC vẫn là một 
hướng nghiên cứu được quan tâm rộng rãi. 
4.2. Giải pháp cho tín hiệu ở dạng điều chế 
4.2.1. Đề xuất giải pháp 
 Hàm ACF của tín hiệu có thể được minh họa bởi: 
 1  1/4  1/4  3/4  3/4 
 RB () tri tri tri tri tri 
 1/44 1/4 1/4 1/4 1/4 
 (4.2) 
 1  1/ 2 1/ 2 
 tri tri 
 2 1/ 4 1/ 4 
 Với là một hàm tam giác có độ rộng , đỉnh tại vị trí và có biên độ bằng . 
 Cũng với cách thức mô hình hóa tương tự, hàm tương quan BOC – PRN (tương quan chéo giữa 
tín hiệu BOC và mã PRN tạo ra ở bộ thu) có thể được minh họa: 
 1  1/4  1/4  3/4  3/4 
 RBOC/ PRN () tri tri tri tri (4.5) 
 4 1/4 1/4 1/4 1/4 
 Thực hiện kết hợp hai hàm tương quan này qua hai giai đoạn. Giai đoạn thứ nhất, thực hiện kết 
hợp: 
  1  1/ 2  1/ 2 
 Rint () RB()() R BOC/ PRN tri tri tri (4.6) 
 1/ 4 2 1/ 4 1/ 4 
 Hình 4.3. Hàm tương quan BOC – PRN và hàm Hình 4.5. Hàm đề xuất và các hàm ACF, 
 ACF của tín hiệu và hiệu của hai AsPECT và SCPC với tín hiệu 
 hàm tương quan này. . 
 Hàm tương quan ở trong (4.6), so với hàm ACF của tín hiệu đã 
không còn hai đỉnh phụ ngoài cùng như minh họa ở Hình 4.3. Do đó, bên cạnh một đỉnh chỉnh, hàm 
tương quan chỉ tồn tại hai đỉnh phụ. Thực hiện tiếp sự kết hợp sau để loại bỏ hoàn toàn các 
đỉnh phụ này: 
 
 RRRRRpro() int ()  int ()  R B ()  BOC / PRN ()  R B ()  BOC / PRN ()2  tri (4.7) 
 1/ 4
 Như vậy, thông qua các phép kết hợp giữa hàm ACF với hàm tương quan BOC – 
PRN, ta đã nhận được một hàm tương quan tổng hợp mới không còn tồn tại các đỉnh phụ. Hàm 
tương quan tổng hợp được sử dụng trong mạch vòng DLL, với các bản sao có độ trễ khác 
 14 
nhau làm đầu vào của bộ so pha. Bên cạnh đó, dạng của hàm tương quan đề xuất cũng được so sánh 
với các hàm tương quan khác như minh họa ở Hình 4.5. Với giải pháp đề xuất, hàm tương quan vẫn 
duy trì đỉnh chính hẹp, đồng thời loại bỏ được các đỉnh phụ. 
4.2.2. Ảnh hưởng của băng thông bộ lọc RF 
 Ở phần trên, hàm tương quan tổng hợp đã không còn các đỉnh phụ. Do vậy, khi triển 
khai bám mã với hàm này, khả năng bị bám nhầm có thể không xảy ra. 
 Tuy nhiên, dưới tác động của bộ lọc RF, các đỉnh tương quan của các hàm ACF tín hiệu 
 bị suy hao, đồng thời, vị trí của các giữa đỉnh phụ của hàm ACF bị lệch so với vị trí cũ. 
Băng thông bộ lọc càng nhỏ thì các đỉnh bị suy hao càng nhiều và sự dịch chuyển của các đỉnh phụ 
hàm ACF tín hiệu càng lớn. Trong khi đó, các đỉnh của hàm tương quan BOC – PRN 
chỉ bị suy hao mà không bị dịch. Khi đó, kết hợp các hàm tương quan này theo (4.7), hàm tương 
quan tổng hợp nhận được tồn tại các đỉnh phụ có biên độ khá nhỏ ở quanh giá trị 
 . 
 Để giảm thiểu ảnh hưởng của bộ lọc RF, ta có thể thực hiện điều chỉnh biên độ của hàm tương 
quan BOC – PRN trong quan hệ với hàm ACF tín hiệu trong (4.7) bằng hệ số 
( ). Khi đó, (4.7) trở thành: 
 Rpro()().()().() RR B  k R BOC// PRN  B  k R BOC PRN  (4.9) 
 Hình 4.8. Hàm tương quan tổng hợp với với các giá trị khác nhau 
 Hình 4.8 minh họa hàm tổng hợp Rpro () dưới ảnh hưởng của bộ lọc đầu cuối RF ứng với các 
giá trị khác nhau của hệ số . Theo quan sát ở hình vẽ, để khử được các đỉnh phụ trong hàm tương 
quan tổng hợp, giá trị của hệ số phụ thuộc vào băng thông của bộ lọc RF. Băng thông càng nhỏ, 
giá trị của càng lớn. 
4.2.3. Đáp ứng bộ so pha 
 Trong trường hợp bám sóng mang chính xác và không có các tác động của sai số bên ngoài nào 
khác, đáp ứng bộ so pha dạng EMLP với hàm đề xuất có thể được viết lại thành: 
 22
 pro P  
 D () RR   (4.11) 
 EMLP pro pro 
 2 2 2 
 Hình 4.9 mô tả hình dạng của đáp ứng bộ so pha dạng EMLP của cấu trúc NC và cấu trúc đề 
xuất ứng với các giá trị khác nhau của băng thông bộ lọc RF. Trong trường hợp này, ở cấu trúc đề 
xuất, giá trị hệ số . Rõ ràng, quan sát hình vẽ, khi băng thông lớn, đáp ứng bộ so pha ở cấu 
trúc đề xuất không có điểm khóa nhầm. Điều đó cũng có nghĩa, mạch vòng không bị khóa ở các 
đỉnh phụ của hàm ACF tín hiệu . Còn với cấu trúc EMLP NC, đáp ứng của bộ so pha 
 15 
xuất hiện bốn điểm khóa nhầm ứng với bốn đỉnh phụ của hàm ACF tín hiệu . Tuy 
nhiên, khi điều chỉnh băng thông giảm xuống, hai điểm khóa nhầm xuất hiện ứng với các đỉnh phụ 
của hàm tương quan tổng hợp. Để đạt được trạng thái loại bỏ hoàn toàn hiện tượng khóa nhầm, ta 
thay đổi giá trị của hệ số như minh họa ở Hình 4.10. Qua mô tả ở hình vẽ, khi giá trị của càng 
lớn thì đáp ứng của bộ so pha càng tiến tới loại bỏ điểm khóa phụ rõ ràng hơn. 
 Hình 4.9. Đầu ra bộ so pha có với Hình 4.10. Điểm khóa phụ bộ so pha của cấu trúc đề 
 của cấu trúc EMLP NC và cấu trúc đề xuất với các giá trị khác nhau và 
 xuất có 
 Hình 4.11. Cấu trúc mạch vòng DLL theo giải pháp đề xuất 
 Trên cơ sở những phân tích ở trên, cấu trúc mạch vòng DLL thực hiện bám mã với giải pháp đề 
xuất được xây dựng như minh họa ở Hình 4.11. Để thuận tiện, ở hình vẽ chỉ minh họa các kênh ứng 
với việc tạo ra các bản sao Sớm, Muộn của các kênh tín hiệu đồng pha. Việc tạo ra hàm tương quan 
tổng hợp được thực hiện trong khối “Kết hợp”. Bên cạnh đó, để giảm ảnh hưởng của hiện tượng sai 
động của tín hiệu đối với hoạt động mạch vòng DLL, đáp ứng của bộ so pha ở PLL cũng được đưa 
đến để điều chỉnh hoạt động của bộ dao động điều khiển số (NCO) ở trong mạch vòng DLL (giải 
pháp “carrier aiding”). 
4.2.4. Ảnh hưởng của tín hiệu đa đường 
 Ảnh hưởng của tín hiệu đa đường đến hiệu năng của mạch vòng DLL phụ thuộc vào biên độ 
tương đối và pha tương đối của tín hiệu đa đường so với tín hiệu LOS. Trong trường hợp chỉ xem 
xét ảnh hưởng của một thành phần tín hiệu đa đườ