Luận án Nghiên cứu phát triển lý thuyết hệ điều khiển nhiều tầng trong điều khiển quá trình nhiệt trên cơ sở chỉ số dao động mềm

Trang 1

Trang 2

Trang 3
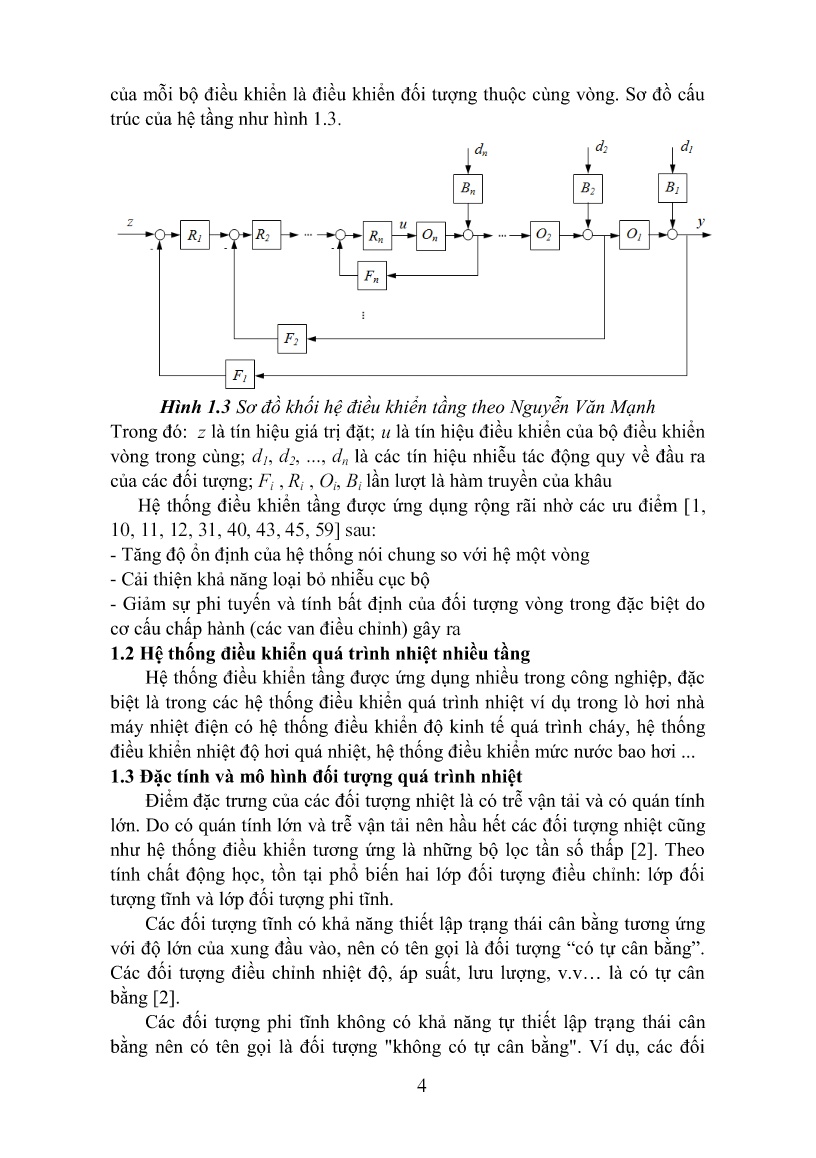
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Luận án Nghiên cứu phát triển lý thuyết hệ điều khiển nhiều tầng trong điều khiển quá trình nhiệt trên cơ sở chỉ số dao động mềm", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Luận án Nghiên cứu phát triển lý thuyết hệ điều khiển nhiều tầng trong điều khiển quá trình nhiệt trên cơ sở chỉ số dao động mềm

phương pháp mô hình nội IMC,
phương pháp bền vững chất lượng cao. Nhưng hiệu quả áp dụng các
phương pháp này còn nhiều hạn chế vì:
- Phương pháp Zigler – Nichol đơn giản nhưng cho độ quá điều chỉnh
của hệ thống kín lớn và dao động nhiều.
- Phương pháp IMC cho chất lượng đáp ứng vòng kín theo kênh đặt tốt
nhưng khả năng kháng nhiễu kém.
- Phương pháp bền vững chất lượng cao cho chất lượng hệ thống tốt cả
với giá trị đặt và nhiễu nhưng bộ điều khiển có cấu trúc phức tạp, khó
thực thi. Phương pháp này cần phải phát triển hoàn thiện hơn khi áp
dụng cho hệ nhiều tầng.
5
CHƢƠNG 2. PHƢƠNG PHÁP NGHIÊN CỨU ĐỘNG HỌC HỆ
TẦNG
2.1 Nền tảng lý thuyết
2.1.1 Chỉ số dao động và dự trữ ổn định của hệ thống
Xét hệ tuyến tính có phương trình đặc tính sau:
nn 1
a01 s a s ... an 0 (2.15)
(2.15) có p nghiệm thực sk = –k và q cặp nghiệm phức si,i+1 = –i ji
mi = βi/ωi gọi là chỉ số dao động của cặp nghiệm phức thứ i.
Cặp nghiệm phức theo chỉ sô dao động là:
(2.16)
si m i i j i
Cặp nghiệm trội là:
sc m c c j c (2.17)
βi
Với mmci min{ } min
ii i
Cặp nghiệm trội làm ảnh hưởng tới quá trình quá độ của hệ thống kéo
dài và tắt chậm và do đó nó quyết định tính ổn định và dự trữ ổn định của hệ
thống. Vậy, chỉ số dao động và hệ số tắt dần của hệ thống được xác định
theo cặp nghiệm trội.
2.1.2 Chỉ số dao động mềm, đường biên mềm và đặc tính mềm
Chỉ số dao động mềm [67] có công thức như sau:
1 e
mm() (2.18)
0
Với α ≥ 0 là hệ số mềm hóa, m0 = const là hệ số hay chỉ số dao động ứng
với tần số ω =0
Khi thay đổi từ đến + , thì s = m||+j biến thiên dọc theo đường
cong MON đối xứng qua trục thực gọi là đường biên mềm (hình 2.3) [67].
Do tính đối xứng nên luận án chỉ xét với 0.
Hình 2.3. Các đường giới hạn nghiệm khác nhau
6
Vì tính đối xứng nên trong luận án sử dụng s = m+j thay cho
s = m||+j để ngầm hiểu là xét với ≥ 0, còn lại khi ≤ 0 sẽ đối xứng
qua trục thực.
Đường biên mềm được áp dụng để xác định dự trữ ổn định của hệ thống
theo vị trí các điểm cực. Nếu tất cả các điểm cực của hệ thống nằm bên trái
hoặc nằm trên đường biên mềm cho trước, thì hệ đó có dự trữ ổn định mềm
[67] cho trước.
Nếu thay s = m+j vào hàm truyền của hệ hở thì được: H(-mω+jω)
gọi là đặc tính mềm của hệ hở [67].
Trường hợp riêng: α =0, khi đó m = m0 = const.
Nếu thay s = m0 +j vào hàm truyền của hệ hở thì được:
H(-m0ω+jω) gọi là đặc tính cứng của hệ hở [67].
2.1.4 Tiêu chuẩn dự trữ ổn định mềm
Giả sử hệ hở có chỉ số dao động mềm cho trước (m0 > 0 và α > 0) tức
các nghiệm đặc tính của nó nằm bên trái đường biên mềm đã cho, tiêu
chuẩn dự trữ ổn định mềm [67] như sau:
Điều kiện cần và đủ để các nghiệm đặc tính của hệ kín và hệ hở cùng
nằm bên trái đường biên mềm cho trước là đặc tính mềm của hệ hở không
bao điểm ( 1,j0).
2.1.5 Ổn định và dự trữ ổn định theo tiêu chuẩn Parabol
2.1.5.1 Tiêu chuẩn ổn định Parabol [68]
Giả sử hệ hở có q nghiệm đặc tính nằm bên phải và n-q nghiệm nằm bên
trái đường biên mềm đã cho.
Tiêu chuẩn parabol 1 : Điều kiện cần và đủ để hệ kín ổn định là đặc tính
tần số của hệ hở cắt nửa dương parabol (P = Q2 1) (Q>0) với số điểm
“cắt ra” nhiều hơn số điểm “cắt vào” là q/2, trong đó q là số điểm cực
phải của hệ hở.
Tiêu chuẩn parabol 2: Nếu hệ hở ổn định, thì điều kiện cần và đủ để hệ
kín ổn định là số điểm “cắt ra” và số điểm “cắt vào” giữa đặc tính tần số
của hệ hở và nửa parabol dương, bằng nhau.
2.1.5.2 Tiêu chuẩn dự trữ ổn định Parabol theo chỉ số dao động mềm [68]
Giả sử hệ hở có q nghiệm đặc tính nằm bên phải và n-q nghiệm nằm bên
trái đường biên mềm đã cho.
Tiêu chuẩn Parabol mở rộng 1: Điều kiện cần và đủ để hệ kín có độ dự
trữ ổn định mềm cho trước là đặc tính mềm của hệ hở tương ứng cắt nửa
dương parabol với số điểm “cắt ra” lớn hơn số điểm “cắt vào” là q/2
Tiêu chuẩn Parabol mở rộng 2: Điều kiện cần và đủ để hệ kín bảo toàn
độ dự trữ ổn định mềm của hệ hở là số điểm “cắt ra” và số điểm “cắt vào”
giữa đặc tính mềm hệ hở và nhánh parabol dương bằng nhau.
2.1.5.3 Điều kiện đủ của tiêu chuẩn Parabol [68]
7
Điều kiện đủ để cho hệ thống kín bảo toàn độ dự trữ ổn định của hệ hở
ban đầu sau khi nối kín các liên hệ ngược từ hệ hở đó, là: Qmax 0 với
max
Q là tung độ điểm “cắt vào’’ cao nhất của đặc tính mềm với nửa dương
parabol P = Q2 1.
2.2 Áp dụng chỉ số dao động mềm để nghiên cứu hệ tầng
2.2.1 Cấu trúc một vòng tương đương của hệ tầng và hàm truyền hở của
hệ thống [CT 1, 4]
Theo sơ đồ cấu trúc của hệ nhiều tầng hình 1.3 ta có thể biến đổi như
sau: Chọn Rk làm một khâu (bộ) điều khiển và biến đổi tương đương để đi
đến sơ đồ hệ một vòng tương đương như hình 2.12.
Trong đó: WK là hàm truyền của hệ tầng trực thuộc tính từ đầu ra của Rk
đến đầu vào của Ok, OTk là hàm truyền tương đương của phần mạch, tính từ
đầu ra của Ok đến đầu vào của Rk
WK OTk
y z -
Rk Rk+1 Rn On Ok+1 Ok Ok-1 Ok-2 O1 F1 R1 Rk-1
- - - - - -
Fn
F2
Fk+1 Fk-1
Fk
Hình 2.12 Sơ đồ hệ một vòng tương đương của hệ tầng, ứng với khâu điều
chỉnh Rk
Hàm truyền của hệ hở ứng với bộ điều chỉnh thứ k là:
k n
FROq i i
q 1 iq
(2.44)
HRWOOk k k k Tk n n
1 FROq i i
qk 1 iq
2.2.2 Đặc tính mềm của hệ tầng và khả năng đánh giá dự trữ ổn định
2.2.2.1 Đặc tính mềm của hệ tầng [CT 1, 4]
Thay s = m+j vào Hk trong công thức (2.44) ta được Hk( m+j)
gọi là đặc tính mềm của hệ hở ứng với khâu điều chỉnh Rk (hay gọi là đặc
tính mềm tầng thứ k).
Đối tượng điều chỉnh của tầng thứ i biểu diễn dưới dạng sau [2]:
b b s b s2 ... b sm e i s
O s 0 1 2 m O s e i s (2.45)
i 1 a s a s2 ... a ssn q iPT
12 n
8
Trong đó: b0 là hệ số truyền; a1,...,am, b1,...,bn là các hệ số; q là bậc tích
phân; m là bậc tử thức; n là bậc mẫu thức; m ≤ n; i là độ trễ của đối tượng
thuộc vòng i; OiPT(s) là phần phân thức thuần túy.
Hàm truyền (2.45) là dạng tổng quát của đối tượng tuyến tính trong
công nghiệp nói chung.
Biến đổi (2.44) và thay s = m +j , ta có công thức đặc tính mềm
của hệ hở tầng thứ k, như sau
k
qqmj
eHq, PT ( m j ) e
H() m j q 1 (2.47)
k n
qqmj
1 e Hq, PT ( m j ) e
qk 1
n
Trong đó: là phần phân thức
Hq, PT()()()() s F q s R i s O iPT s
iq
n
là tổng độ trễ vận tải của các khâu thuộc các vòng từ
qi
iq
thứ q đến n
2.2.2.2 Sự hội tụ của đặc tính mềm và khả năng đánh giá dự trữ ổn định hệ
tầng
Giới hạn môđun của đặc tính mềm là:
limHk ( m j ) 0 (2.51)
Với giả thiết đặc tính mềm không chứa điểm cực của hệ hở thì điều
kiện (2.51) chứng tỏ rằng đặc tính mềm của hệ hở nhiều tầng hội tụ về gốc
toạ độ. Vậy có thể áp dụng tiêu chuẩn dự trữ ổn định mềm và tiêu chuẩn
Parabol để đánh giá động học cho hệ thống điều khiển tầng trong trường
hợp đặc tính mềm là đặc tính mềm của hệ tầng hở.
2.2.3 Phương pháp xác định cặp nghiệm trội của hệ tầng
Để tìm nghiệm đặc tính của hệ thống ta chỉ việc đưa đặc tính mềm đi
qua điểm ( 1;j0) bằng cách thay đổi chỉ số dao động mềm thông qua việc
thay đổi giá trị m0 trong công thức (2.18). Giá trị cặp nghiệm trội được xác
định khi đặc tính mềm đi qua điểm ( 1;j0) ứng với giá trị tần số cắt c nhỏ
nhất và m0 nhất định [CT 1].
2.4 Kết luận
- Rút ra công thức đặc tính mềm của hệ tầng hở cho các hệ thống điều khiển
nhiều tầng có trễ vận tải trong công nghiệp trong đó có quá trình nhiệt.
- Chứng minh được đặc tính mềm của hệ tầng hở hội tụ về gốc tọa độ, cho
phép áp dụng các tiêu chuẩn dự trữ ổn định mềm và tiêu chuẩn Parabol để
đánh giá dự trữ ổn định của hệ điều khiển nhiều tầng. Như vậy có thể dùng
9
đặc tính mềm để đánh giá tính ổn định cũng như chất lượng đáp ứng của hệ
thống điều khiển tầng.
- Trên cơ sở áp dụng đặc tính mềm có thể xác định các nghiệm đặc tính
trong đó có nghiệm trội của hệ tầng. Từ đó cũng có thể đánh giá dự trữ ổn
định của hệ thống bằng cách đánh giá vị trí cặp nghiệm trội của hệ thống so
với đường biên mềm cho trước trên mặt phẳng nghiệm của đa thức đặc tính.
CHƢƠNG 3. PHƢƠNG PHÁP CHỈNH ĐỊNH HỆ TẦNG DỰA TRÊN
CHỈ SỐ DAO ĐỘNG MỀM
3.1 Nền tảng lý thuyết
3.1.2 Hệ thống bền vững
Hàm truyền của hệ thống bền vững nhất [4, 69] là:
K
Ws( ) , 0 (3.1)
1 θs
K là hệ số truyền; là hằng số quán tính lớn hơn không.
Hàm truyền hệ hở tương ứng [4, 69] :
K
Hs() (3.2)
1 K θs
Theo [4, 69], chỉ có thể chọn K 1.
3.1.3 Hệ thống bền vững chất lượng cao
Hàm truyền hệ điều khiển bền vững chất lượng cao [4, 69] là:
1
Ws( ) ,θ 0 (3.6)
1 θs
Với 0 thì W(s) 1.
Hàm truyền của hệ hở bền vững chất lượng cao [4, 69] là :
1
Hs() (3.7)
θs
Hàm truyền của bộ điều chỉnh [4, 69], là:
1
R( s ) O ( s ) 1 (3.8)
θs
Theo [4], bộ điều khiển bền vững có thể được thực thi bằng cách cắt bỏ
thành phần trễ của đối tượng. Khi đó bộ điều khiển trong (3.8) có dạng:
1
R( s ) O ( s ) 1 (3.9)
θs PT
OPT(s) là hàm truyền của đối tượng sau khi bỏ thành phần trễ.
3.2 Phƣơng pháp tổng hợp bền vững hệ điều khiển tầng [CT 2, 5]
Các bộ điều khiển trong hệ nhiều tầng sẽ xác định được trên cơ sở quan
điểm tổng hợp hệ bền vững chất lượng cao. Một hệ điều khiển tầng là bền
vững chất lượng cao nếu nó đảm bảo tính chất bền vững chất lượng cao đối
với mỗi hệ một vòng tương đương.
10
Với yêu cầu mỗi hệ một vòng tương đương đều có cấu trúc bền vững
chất lượng cao trên cơ sở (3.7). Như từng hệ một vòng tương đương phải
thoả mãn điều kiện:
1
(3. 10)
Hk
θsk
Hk là hàm truyền hệ hở vòng thứ k, θk là hằng số quán tính.
Không mất tính tổng quát, giả sử Fk =1.
Để tìm Rk thì từ (2.44) cần phải giải hệ phương trình sau:
k n
ROii
j 1 ij (3.12)
n n Hk , k 1, n
1 ROii
jk 1 ij
Từ (3.10) và (3.12) ta được:
1 2s 1
RO11
12 s
...
(3.26)
1 ns n 21 n 1
ROnn 11
n 12 n 1 n s
nn 1 1
ROnn
nn 1 1s
Từ hệ phương trình (3.26) ta thấy các bộ điều khiển R tại mỗi tầng của hệ
nhiều tầng chỉ phụ thuộc vào các hệ số θk của hai vòng liền kề θk-1, θk+1 và
đối tượng thuộc vòng đó. Để có các bộ điều khiển thì cần phải xác định các
hệ số θk.
Xét trường hợp hệ thống điều khiển quá trình nhiệt:
Trong các hệ thống điều khiển các quá trình nhiệt, độ tác động nhanh của
vòng trong lớn hơn hẳn so với vòng ngoài (tức là độ quán tính và độ trễ của
vòng trong nhỏ hơn hẳn so với vòng ngoài) do đó vòng trong làm việc ở dải
tần cao hơn nhiều so với vòng ngoài. Khi vòng trong tác động thì vòng
ngoài hầu như chưa phản ứng và thể hiện như một mạch đứt. Trong trường
hợp này, công thức (3.26) được đơn giản hóa như sau:
1 1
RO11
1s
...
(3.27)
1 1
ROnn 11
n 1s
1 1
ROnn
ns
11
(3.26) và (3.27) gọi là các bộ điều khiển bền vững lý tưởng và công thức
(3.27) được sử dụng để tổng hợp hệ thống điều khiển quá trình nhiệt.
3.3 Thực thi bộ điều khiển bền vững
Khi đối tượng có thời gian trễ (τ > 0), các bộ điều khiển theo công thức
(3.27) không thực thi được bởi vì nó sẽ chứa khâu dự báo tuyệt đối (thành
phần trễ dương). Theo [4], để đơn giản nhất khi thực thi là loại bỏ thành
phần trễ này trong công thức của các bộ điều khiển. Khi đó hàm truyền các
bộ điều khiển ở công thức (3.27) như sau:
1 1
Rk()() s O kPT s (3.30)
k s
Với OkPT là phần phân thức của Ok.
Mặt khác nếu n +q >1 (n, q trong công thức (1.2) thì bộ điều khiển bền
vững sẽ có hàm truyền bậc của tử số lớn hơn bậc của mẫu số. Nếu trường
hợp này xảy ra cần phải bù bậc cho bộ điều khiển bằng cách mắc nối tiếp bộ
điều khiển với khâu lọc [CT 5] có hàm truyền:
1
(3.31)
k ()s nq 1
(1 0,1Tsmin )
Với: n, q là hằng số trong công thức (1.2)
Tmin là hằng số thời gian nhỏ nhất của đối tượng Ok(s).
Bộ điều khiển bền vững khả thi có cấu trúc là:
1 1
Rk()()() s O kPT s s (3.32)
k s
*) Một số trường hợp điển hình:
- Nếu hàm truyền của đối tượng vòng thứ k bất kỳ là khâu quán tính bậc
nhất thì bộ điều khiển bền vững có dạng PI.
- Nếu hàm truyền đối tượng vòng thứ k bất kỳ là khâu quán tính – tích phân
bậc nhất có trễ thì bộ điều khiển bền vững có dạng PD.
- Nếu hàm truyền đối tượng vòng thứ k bất kỳ là khâu quán tính bậc hai có
trễ thì bộ điều khiển bền vững có dạng PID.
3.4 Phƣơng pháp xác định các hệ số bộ điều khiển theo chỉ số dao động
mềm [CT 3]
Phần này thực hiện lựa chọn các hệ số θk ở công thức (3.30). Để tạo ra
mối liên hệ giữa bộ điều khiển với dự trữ ổn định của hệ thống và thời gian
trễ của đối tượng, trong mục này tác giả luận án đưa ra một phương pháp
tạo ra mối quan hệ giữa các hệ số của bộ điều khiển với chỉ số dao động
mềm và thời gian trễ của đối tượng. Công thức như sau:
emck arccot m ck
k (3.63)
k 2
arccot mck m ck 1
12
mck là chỉ số dao động cắt ở vòng thứ k; τk và thời gian trễ của đối
tượng vòng thứ k.
*) Lựa chọn chỉ số dao động cho các vòng [CT 3]
Đối với hệ nhiều tầng yêu cầu chất lượng được xác định cho tín hiệu ra
ở vòng ngoài cùng. Tức là chỉ số dao động m1 ở vòng ngoài cùng là theo
yêu cầu chất lượng hệ thống, còn chỉ số dao động của các vòng trong là
chưa biết. Độ bền vững của vòng trong phải tốt hơn hay ít nhất cũng bằng
vòng ngoài, khi đó chỉ số dao động của vòng trong lớn hơn hoặc bằng chỉ số
dao động của vòng ngoài (mi+1 ≥ mi).
3.5 Chỉnh định lại hệ số khuếch đại của các bộ điều khiển [CT4, 5]
Trong khi tính toán hệ thống, có thể xảy ra trường hợp hệ thống thiếu
dự trữ ổn định hoặc thừa dự trữ ổn định. Vậy phải điều chỉnh hệ thống sao
cho hệ thống vừa đủ dự trữ ổn định cho trước. Đối với hệ thống điều khiển
tầng, để hệ thống vừa đủ dự trữ ổn định cho trước cần phải thì cần điều
chỉnh lại hệ số khuếch đại của bộ điều khiển để đặc tính mềm của hệ hở
tương ứng đi qua điểm (-1, j0).
3.6 Các bƣớc thực hiện chỉnh định hệ thống điều khiển tầng
3.6.1 Trình tự tính toán các bộ điều chỉnh bền vững trong hệ nhiều tầng
Bước 1: Tính toán cho vòng ngoài cùng (k =1)
- Theo yêu cầu chất lượng đã cho, xác định chỉ số dao động cắt của vòng
ngoài cùng mc1 cần thiết.
- Tính hằng số quán tính θ1 theo công thức (3.63) với k =1.
Bước 2: Tính toán cho vòng thứ 2 (k =2)
- Chọn chỉ số dao động cắt cho vòng này (mc2) sao cho mc2 ≥ mc1.
- Tính hằng số quán tính θ2 theo công thức (3.63) với k =2.
Bước 3: Nếu hệ thống có n tầng (n>2) thì lặp lại việc tính toán cho từng
vòng theo bước 2 với việc chọn chỉ số dao động vòng trong lớn hơn vòng
ngoài kế tiếp.
Bước 4: Tính toán khâu bù bậc cho các bộ điều khiển theo công thức (3.31).
Thay các hệ số θk tính toán ở các bước trên và khâu bù bậc vào công thức
(3.32) ta được các bộ điều khiển bền vững.
Bước 5: Cho trước m0 và α trong công thức của đặc tính mềm (2.18) để xác
định đường biên mềm hay độ dự trữ ổn định cho trước của hệ thống.
Vẽ các đặc tính mềm hệ hở tương ứng với các vòng. Nếu đặc tính mềm
của hệ hở tương ứng với vòng nào đó bao điểm (-1, j0) thì thực hiện chỉnh
định lại hệ số khuếch đại của bộ điều khiển của vòng đó để hệ thống vừa đủ
dự trữ ổn định.
Cuối cùng vẽ đáp ứng quá độ của hệ thống theo kênh đặt và theo kênh
nhiễu để đánh giá chất lượng của hệ thống.
13
3.6.2 Trình tự tính toán các bộ điều khiển bền vững dưới dạng PID (bộ
PID bền vững) trong hệ nhiều tầng
Bước 1: Tính toán cho vòng ngoài cùng (k =1)
'
- Mô hình hóa các đối tượng trong hệ tầng O1 thành O1 có dạng hàm truyền
là các khâu quán tính bậc nhất có trễ, khâu quán tính – tích phân bậc nhất có
trễ hoặc khâu quán tính bậc hai có trễ. Nếu đối tượng O1 có dạng hàm
truyền là khâu trên thì không cần phải thực hiện mô hình hóa, lúc này
'
OO11 .
- Theo yêu cầu chất lượng đã cho, xác định chỉ số dao động cắt của vòng
ngoài cùng mc1 cần thiết.
- Tính hằng số quán tính θ1 theo công thức (3.63) với k =1.
Lưu ý hằng số thời gian trễ trong công thức (3.63) là hằng số thời gian
'
trễ của đối tượng O1 .
Bước 2: Tính toán cho vòng thứ 2 (k =2)
'
- Mô hình hóa các đối tượng trong hệ tầng O2 thành O2 có dạng hàm truyền
là các khâu quán tính bậc nhất có trễ, khâu quán tính – tích phân bậc nhất có
trễ hoặc khâu quán tính bậc hai có trễ. Nếu đối tượng O2 có dạng hàm
truyền là khâu trên thì không cần phải thực hiện mô hình hóa, lúc này
'
OO22 .
- Chọn chỉ số dao động cắt cho vòng này (mc2) sao cho mc2 ≥ mc1.
- Tính hằng số quán tính θ2 theo công thức (3.63) với k =2.
Lưu ý hằng số thời gian trễ trong công thức (3.63) là hằng số thời gian
'
trễ của đối tượng O2 .
Bước 3: Nếu hệ thống có n tầng (n>2) thì lặp lại việc tính toán cho từng
vòng theo bước 2 với việc chọn chỉ số dao động vòng trong lớn hơn vòng
ngoài kế tiếp.
Bước 4: Thay các hệ số θk tính toán được ở các bước trên vào công thức
(3.30) để đưa ra công thức các bộ điều khiển bền vững dưới dạng PID.
'
Chú ý là các đối tượng Ok trong công thức (3.30) là các đối tượng Ok .
Bước 5: Cho trước m0 và α trong công thức của đặc tính mềm (2.18) để xác
định đường biên mềm hay độ dự trữ ổn định cho trước của hệ thống.
Vẽ các đặc tính mềm hệ hở tương ứng với các vòng. Nếu đặc tính mềm
của hệ hở tương ứng với vòng nào đó bao điểm (-1, j0) thì thực hiện chỉnh
định lại hệ số khuếch đại của bộ điều khiển của vòng đó để hệ thống vừa đủ
dự trữ ổn định.
14
Cuối cùng vẽ đáp ứng quá độ của hệ thống theo kênh đặt và theo kênh
nhiễu để đánh giá chất lượng của hệ thống.
3.6.3 Trường hợp hệ hai tầng
Xét hệ thống với cấu trúc điều khiển hai tầng hình 3.4.
V1
z y
R1 R2 O2 O1
- -
Hình 3.4 Sơ đồ hệ một vòng tương đương ứng với bộ điều khiển R1
Cách 1: Xác định các bộ điều khiển theo đối tượng từng vòng, tức là sử
dụng công thức các bộ điều khiển trong (3.32). Trình tự tính toán các bộ
điều khiển bền vững giống như mục 3.6.1 hoặc tính toán các bộ PID bền
vững giống như mục 3.6.2.
Cách 2: Xác định bộ điều khiển vòng trong theo đối tượng vòng trong (sử
dụng công thức (3.35)), bộ điều khiển vòng ngoài theo đối tượng tương
đương V1 thể hiện trên hình 3.7.
Từ hình 3.7, hàm truyền của đối tượng tương đương V1 là:
ROO2 2 1
V1 (3.67)
1 RO22
Với V1PT là hàm truyền của V1 sau khi bỏ trễ. Tổng hợp bộ điều khiển
R1 theo quan điểm bền vững [4, 74] sẽ được:
1 1
R11()() s VPT s (3.68)
1s
θ1 tính theo công thức (3.63) với τ trong công thức này là thời gian trễ
của đối tượng tương đương V1.
Trình tự tính toán các bộ điều khiển bền vững trong trường hợp này
được thực hiện như sau:
Bước 1: Tính toán cho vòng trong (tầng thứ 2 ứng với k =2)
- Chọn chỉ số dao động cắt cho vòng này (mc2).
- Tính hằng số quán tính θ2 theo công thức (3.63) với k =2.
Lưu ý hằng số thời gian trễ trong công thức (3.63) là hằng số thời gian
trễ của đối tượng O2.
- Tính toán khâu bù bậc cho bộ điều khiển vòng trong theo công thức (3.31).
- Thay hệ số θ2 và khâu bù bậc vào công thức (3.32) ta được bộ điều khiển
bền vững cho vòng trong.
15
Bước 2: Tính toán cho vòng ngoài (k =1)
- Tính hàm truyền của đối tượng tương đương V1 theo công thức (3.67).
- Chọn chỉ số dao động cắt cho vòng này (mc1): mc1 ≤ mc2
- Tính hằng số quán tính θ1 theo công thức (3.63) với k =1.
Lưu ý thời gian trễ trong công thức (3.63) là thời gian trễ của đối tượng V1.
- Tính toán khâu bù bậc cho bộ điều khiển vòng ngoài theo công thức
(3.31).
- Thay hệ số θ1 và khâu bù bậc vào công thức (3.32) ta được bộ điều khiển
bền vững cho vòng ngoài.
Bước 3: Cho trước m0 và α trong công thức của đặc tính mềm (2.18) để xác
định đường biên mềm hay độ dự trữ ổn định cho trước của hệ thống.
Vẽ các đặc tính mềm hệ hở tương ứng với các vòng. Nếu đặc tính mềm
của hệ hở tương ứng với vòng nào đó bao điểm (-1, j0) thì thực hiện chỉnh
định lại hệ số khuếch đại của bộ điều khiển của vòng đó để hệ thống vừa đủ
dự trữ ổn định.
Cuối cùng vẽ đáp ứng quá độ của hệ thống theo kênh đặt và theo kênh
nhiễuFile đính kèm:
 luan_an_nghien_cuu_phat_trien_ly_thuyet_he_dieu_khien_nhieu.pdf
luan_an_nghien_cuu_phat_trien_ly_thuyet_he_dieu_khien_nhieu.pdf

