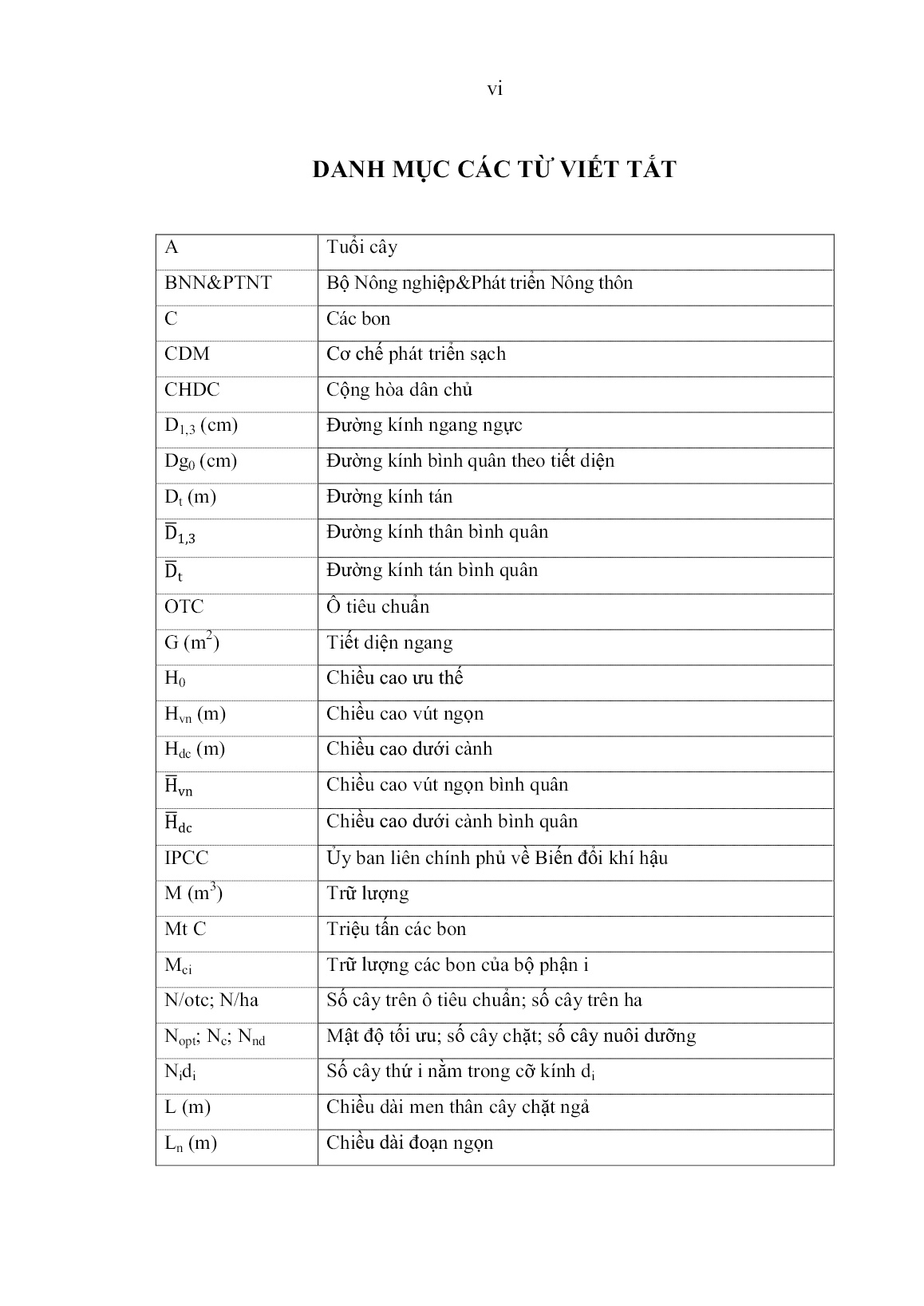
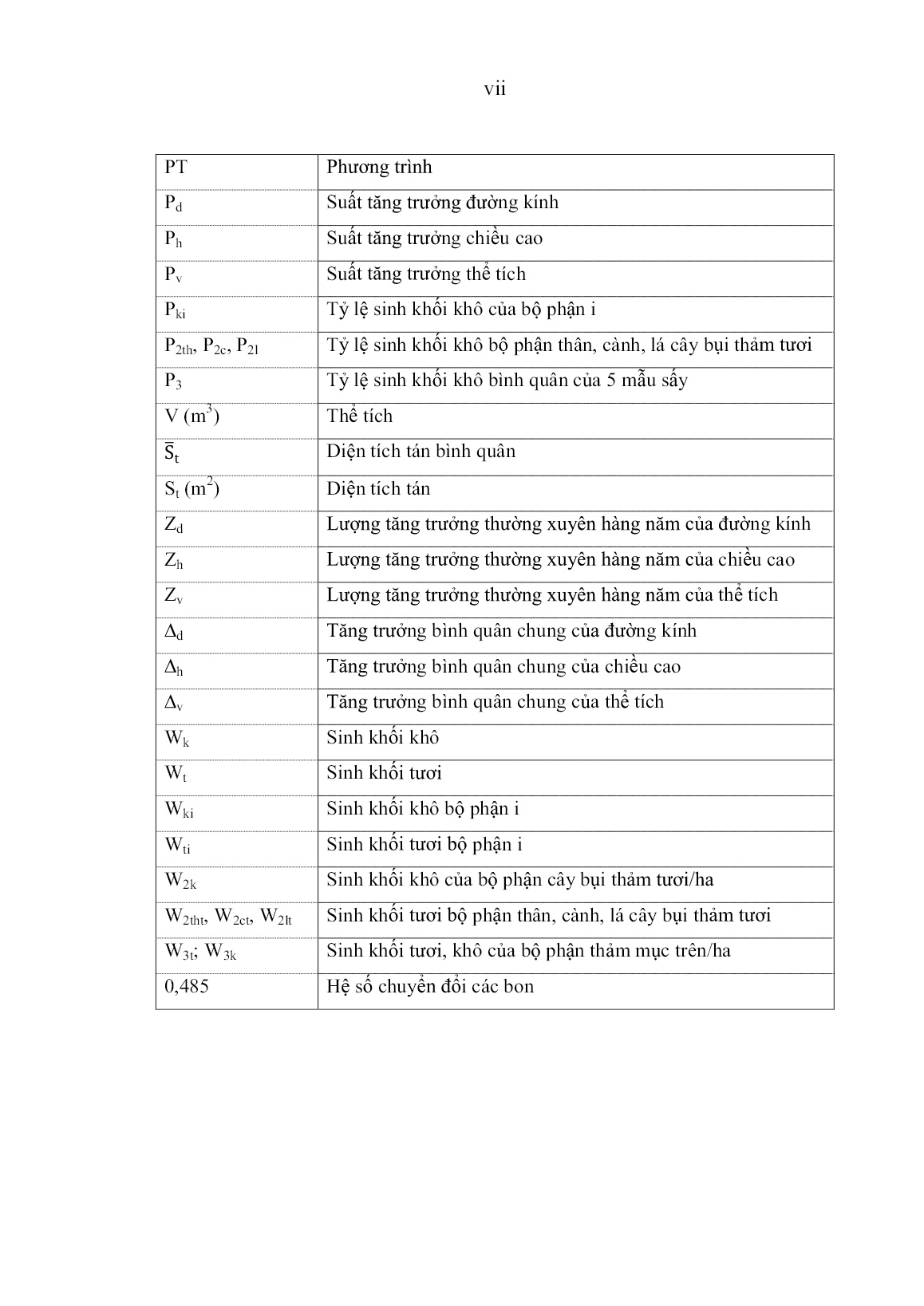
Luận án Nghiên cứu sinh trưởng và cấu trúc làm cơ sở khoa học đề xuất biện pháp kỹ thuật góp phần kinh doanh rừng trồng tếch (Tectona grandis L. F.) tại Sơn La

 thưa khi nuôi 
dưỡng rừng trồng Tếch tại khu vực nghiên cứu. 
4.4. Nghiên cứu sinh trƣởng, tăng trƣởng rừng trồng Tếch 
Khi nghiên cứu sinh trưởng cây cá lẻ và lâm phần cần quan tâm đến mọi yếu tố 
ảnh hưởng đến quá trình sinh trưởng. Có rất nhiều nhân tố tác động. Nhân tố bên trong 
bao gồm: nhân tố di truyền, biến dị, khả năng thích ứng, khả năng đồng hóa - dị hóa, 
khả năng cạnh tranh với môi trường. Các nhân tố bên ngoài có thể kể đến như là: khí 
 77 
hậu thời tiết, thủy văn, lửa rừng, địa hình, địa chất, đất đai, kỹ thuật gây trồng và kinh 
doanh, nuôi dưỡng và các hoạt động khác của con người. Mỗi nhân tố trên lại chứa 
đựng rất nhiều yếu tố thành phần tác động, ảnh hưởng đến toàn bộ đời sống cây rừng. 
Nhiều công trình khoa học đã nghiên cứu quan hệ giữa cây rừng và rừng với 
các nhân tố ngoại cảnh đều cho rằng mọi hoạt động sống của rừng có mối quan hệ 
mật thiết với môi trường xung quanh. Nhưng không thể đồng thời một lúc có thể 
nghiên cứu hết các nhân tố tác động tới sinh trưởng của cây. Nhiều nhà khoa học đã 
tìm cách khống chế, tách, gộp, cố định một số nhân tố để xem xét ảnh hưởng của 
từng nhân tố chính nào đó mà thôi. Tuy nhiên, khi cô lập một nhân tố nào đó khó 
tránh khỏi những sai số do sự chủ định cô lập hóa của nhà nghiên cứu gây ra. Do 
đó, tính độc lập ở đây cũng chỉ mang ý nghĩa tương đối và nhà nghiên cứu cố gắng 
tìm cách loại trừ các sai số đó. Đề tài chủ yếu quan tâm đến ba chỉ tiêu sinh trưởng 
là sinh trưởng đường kính (D1,3), chiều cao (Hvn) và thể tích (V) của cây rừng, xem 
xét chúng trong mối quan hệ mật thiết với cấp đất. 
4.4.1. Khảo sát các hàm sinh trưởng 
Để xác định quy luật sinh trưởng từng đại lượng D, H, V cho cây bình quân 
trên cấp đất II và III từ số liệu thực nghiệm. Tác giả đã sử dụng hàm Gompertz và 
Schumacher để mô tả và được tổng hợp ở bảng 4.18. 
Bảng 4.18. Số liệu cây bình quân trên cấp đất II và III 
Cấp đất II Cấp đất III 
A D H V A D H V 
1 0,00 0,72 0,00005 1 0,00 0,66 0,00005 
2 3,84 1,93 0,0013 2 2,41 1,57 0,00114 
3 5,02 2,82 0,0054 3 4,19 2,5 0,00443 
4 6,76 4,12 0,01256 4 5,25 3,65 0,00995 
5 8,18 5,37 0,02233 5 6,33 4,88 0,01727 
6 9,44 6,95 0,03411 6 7,29 6,27 0,02594 
7 10,56 8,13 0,04738 7 8,21 7,66 0,03558 
8 11,40 9,32 0,06174 8 9,29 8,71 0,04589 
9 12,37 10,44 0,07686 9 10,21 9,75 0,05666 
10 13,19 11,51 0,09248 10 11,10 10,64 0,06772 
11 13,47 12,29 0,10843 11 11,67 11,32 0,07894 
12 14,88 12,73 0,12456 12 12,78 11,55 0,09023 
13 15,74 12,92 0,14075 13 13,72 11,7 0,10153 
 78 
Từ số liệu thực nghiệm, đã so sánh kết quả phân tích số liệu của các hàm lý 
thuyết, từ đó chọn hàm phù hợp nhất để mô tả quy luật sinh trưởng đường kính 
(D1,3), chiều cao (Hvn) và thể tích (V) bằng tiêu chuẩn R
2
. Kết quả được trình bày 
trong bảng 4.19. 
Bảng 4.19. So sánh sự phù hợp của hàm lý thuyết mô tả quy luật 
sinh trƣởng D, H, V bằng tiêu chuẩn R2 
Cấp 
đất II 
Hàm Gompertz 
Y = b0*exp(-b1*exp(-b2*A)) 
Hàm Schumacher 
Y = b0*exp(-b1/A^b2) 
Hàm y/x m b c R
2
 m b C R
2
D 16,05 2,89 0,28 0,977 48,12 3,57 0,54 0,983 
H 14,93 3,64 0,25 0,998 53,03 4,53 0,50 0,994 
V 0,294 6,56 0,20 0,999 2,46 10,84 0,50 0,999 
Phương trình mô tả sinh trưởng 
D = 16,05*exp(-2,89*exp(-0,28*A)) 
H = 14,93*exp(-3,64*exp(-0,25*A)) 
V = 0,294*exp(-6,56*exp(-0,202*A)) 
Phương trình mô tả sinh trưởng 
D = 48,12*exp(-3,57/A^0,54) 
H = 53,03*exp(-4,53/A^0,50) 
V = 2,46*exp(-10,84/A^0,50) 
Cấp 
đất 
III 
Hàm Gompertz Hàm Schumacher 
Hàm y/x m b c R
2
 m b C R
2
D 15,18 2,95 0,23 0,981 79,86 4,52 0,36 0,993 
H 13,25 3,94 0,28 0,998 31,73 5,12 0,64 0,992 
V 0,248 6,55 0,201 0,999 1,94 10,43 0,59 0,999 
Phương trình mô tả sinh trưởng 
D = 15,18*exp(-2,95*exp(-0,23*A)) 
H = 13,25*exp(-3,94*exp(-0,28*A)) 
V = 0,248*exp(-6,55*exp(-0,201*A)) 
Phương trình mô tả sinh trưởng 
D = 79,86*exp(-4,52/A^0,36) 
H = 31,73*exp(-5,12/A^0,64) 
V = 1,94*exp(-10,433/A^0,59) 
Khi khảo sát hai hàm cơ bản này cho thấy, mọi chỉ số sinh trưởng tăng trưởng 
đều thể hiện từ hàm cơ bản tức hàm sinh trưởng Y có thể tính được hàm tăng trưởng 
hay tốc độ sinh trưởng Y’ ở bất kỳ thời điểm Ta nào, từ đó tính được lượng tăng 
 79 
trưởng tối đa Y’max, xác định được điểm uốn sinh trưởng và các giá trị Y, X của điểm 
uốn khi Y’’= 0, suy diễn được tăng trưởng bình quân ∆y, và các hàm suất tăng trưởng 
Py = Y’/Y. 
Kết quả bảng 4.19 cho thấy, cả hai hàm lý thuyết đều mô tả tốt quá trình sinh 
trưởng D, H, V cho cây bình quân trên hai cấp đất với hệ số xác định rất cao, R2 từ 
0,981 - 0,999. Tuy nhiên, hàm Gompertz có nhược điểm là đồ thị mô tả quá trình 
sinh trưởng các nhân tố điều tra không xuất phát từ gốc tọa độ, khi X = 0 thì Y = 
m.e
-a 
> 0, còn hàm Schumacher có ưu điểm là các đồ thị mô tả quá trình sinh trưởng 
xuất phát từ gốc tọa độ 0 (0,0), có một điểm uốn, có một tiệm cận nằm ngang đáp 
ứng được yêu cầu biểu thị một đường cong sinh trưởng. 
Hàm Schumacher cũng đã được các tác giả Trinh Đức Huy (1988) [27], Lê 
Hồng Phúc (1996) [47], Bùi Việt Hải (1996) [12] dùng mô tả sinh trưởng chiều cao 
làm cơ sở lập biểu cấp đất cho loài cây Thông ba lá, Bồ đề. Vũ Tiến Hinh và cộng 
sự (2000) [18] khi lập biểu sinh trưởng và sản lượng cho loài cây Sa mộc, Thông 
đuôi ngựa, Mỡ ở các tỉnh phía Bắc và Đông Bắc Việt Nam đã chọn hàm Gompetz 
để mô tả quy luật sinh trưởng D, H, V cho cây bình quân theo đơn vị cấp đất. Võ 
Đại Hải và cộng sự (2008) [10] đã áp dụng các hàm Gompetz, Schumacher và Jhon 
- Schumacher để mô tả quy luật sinh trưởng D, H, V theo đơn vị tuổi và cấp đất cho 
các loài Thông mã vĩ, Thông nhựa, Thông ba lá, Keo lai, Keo lá tràm, Mỡ và Bạch 
đàn Urophylla trồng thuần loài ở Việt Nam. 
Khi nghiên cứu hai hàm sinh trưởng trên đối tượng rừng Thông ba lá, 
Nguyễn Ngọc Lung và Đào Công Khanh (1999) [37] cũng có nhận xét tương tự. 
Sau đó, tác giả dùng hàm Schumacher mô tả D, H, V cây bình quân theo đơn vị 
cấp đất làm cơ sở lập biểu sản lượng cho rừng Thông ba lá, vì hàm sinh trưởng 
này xuất phát từ gốc tọa độ. 
Từ kết quả thử nghiệm ở trên, đề tài đã chọn hàm Schumacher để mô tả quy luật 
sinh trưởng, tăng trưởng các nhân tố D, H, V cho cây bình quân theo đơn vị cấp đất 
rừng trồng Tếch thuần loài tại Sơn La. 
 80 
4.4.2. Nghiên cứu sinh trưởng, tăng trưởng đường kính 
4.4.2.1. Sinh trưởng đường kính 
Để làm rõ quá trình sinh trưởng đường kính thân cây, trước hết cần phải xây 
dựng mô hình biểu diễn mối quan hệ giữa D1,3 với tuổi cây (A, năm). Sau đó giải 
tích mô hình dự đoán tăng trưởng thường xuyên hàng năm (Zd, cm/năm), lượng 
tăng trưởng bình quân chung (∆d, cm/năm) và suất tăng trưởng hàng năm (Pd,%). 
Để mô tả quá trình sinh trưởng, tác giả đã sử dụng hàm Schumacher. Kết quả được 
trình bày trong bảng 4.20. 
Bảng 4.20. Mô hình sinh trƣởng 𝐃 rừng trồng Tếch bằng hàm Schumacher 
Cấp 
đất 
Tham số của phƣơng trình 
Phƣơng trình sinh trƣởng 
Số hiệu 
PT m b c R
2
II 48,126 3,571 0,540 0,983 D =48,126*exp(3,571/A**0,440) 4.1 
III 79,864 4,521 0,369 0,993 D =79,864*exp(4,621/A**0,369) 4.2 
Từ phương trình (4.1-4.2) xác định đường cong sinh trưởng D của rừng trồng 
Tếch trên hai cấp đất cho khu vực Sơn La. Những giá trị sinh trưởng 𝐷 từ tuổi 14 
trở lên là giá trị nội suy và chỉ có ý nghĩa tham khảo để phân tích và dự đoán chiều 
hướng sinh trưởng đường kính. Quá trình này được mô phỏng trong hình 4.8. 
Hình 4.8. Đường cong sinh trưởng 𝑫 trên cấp đất II và III rừng trồng Tếch 
0
5
10
15
20
25
30
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Tuổi (A)
D1,3 (cm)
Dbq (II)
Dbq(III)
 81 
4.4.2.2. Tăng trưởng đường kính 
Căn cứ vào phương trình (4.1-4.2), tính lượng tăng trưởng thường xuyên và 
tăng trưởng định kỳ đường kính Zd, ∆d. Khi giải phương trình (4.1-4.2), có thể xác 
định được những đại lượng như sau: 
- Ở cấp đất II: Zd= 48,126*3,571*0,440*A^(-0,440-1)*exp(-3,571*A^(-0,440)) 
 ∆d = (48,126*exp(-0,440/A^3,571))/A 
- Cấp đất III: Zd= 79,864*4,621*0,369*A^(-0,369-1)*exp(-4,621*A^(-0,369)) 
 ∆d = (79,864*exp(-4,621/A^0,369))/A 
Kết quả tăng trưởng đường kính trên hai cấp đất trình bày trong bảng 4.21. 
Bảng 4.21. Sinh trƣởng và tăng trƣởng đƣờng kính rừng trồng Tếch 
Cấp đất II Cấp đất III 
A 
𝐃𝟏,𝟑 
(cm) 
Zd 
(cm/n) 
∆d 
(cm/n) 
Pd% A 
𝐃𝟏,𝟑 
(cm) 
Zd 
(cm/n) 
∆d 
(cm/n) 
Pd% 
1 0 2,00 1,35 1 1 0 1,34 0,78 1 
2 3,83 2,12* 1,73 60,88 2 2,41 1,38 1,11 64,75 
3 5,00 1,71 1,77* 34,95 3 4,19 1,47* 1,22 42,36 
4 6,76 1,47 1,72 23,03 4 5,25 1,27 1,25* 26,67 
5 8,17 1,28 1,65 16,59 5 6,33 1,17 1,24 19,66 
6 9,43 1,13 1,58 12,68 6 7,29 1,07 1,22 15,29 
7 10,55 1,00 1,50 10,09 7 8,21 0,99 1,19 12,35 
8 11,40 0,90 1,43 8,29 8 9,29 0,92 1,16 10,26 
9 12,24 0,82 1,37 6,96 9 10,21 0,86 1,13 8,72 
10 13,19 0,75 1,31 5,96 10 11,1 0,80 1,10 7,53 
11 13,46 0,69 1,26 5,18 11 11,67 0,75 1,07 6,60 
12 14,84 0,63 1,21 4,56 12 12,78 0,71 1,04 5,84 
13 15,73 0,59 1,16 4,05 13 13,72 0,67 1,02 5,23 
14 16,62 0,55 1,12 3,63 14 14,66 0,64 0,99 4,72 
15 17,51 0,51 1,08 3,28 15 15,6 0,60 0,97 4,29 
16 18,4 0,48 1,04 2,99 16 16,53 0,58 0,94 3,92 
17 19,29 0,45 1,01 2,73 17 17,47 0,55 0,92 3,60 
18 20,18 0,43 0,98 2,51 18 18,41 0,53 0,90 3,33 
19 21,06 0,40 0,95 2,32 19 19,35 0,50 0,88 3,09 
20 21,95 0,38 0,92 2,15 20 20,29 0,48 0,86 2,88 
21 22,84 0,37 0,90 2,00 21 21,23 0,46 0,84 2,69 
22 22,73 0,35 0,87 1,87 22 22,16 0,45 0,82 2,52 
23 24,61 0,34 0,85 1,75 23 23,10 0,43 0,81 2,37 
24 25,50 0,32 0,83 1,65 24 24,04 0,42 0,79 2,23 
25 26,39 0,31 0,81 1,55 25 24,98 0,40 0,78 2,11 
 82 
Kết quả bảng 4.21 cho thấy, đường kính thân cây Tếch sinh trưởng khá nhanh 
trong 7 năm đầu sau khi trồng, tăng trưởng mạnh nhất ở tuổi 2 - 3, sau đó tăng 
trưởng chậm dần, cụ thể như sau: 
Ở cấp đất II, lượng tăng trưởng thường xuyên hàng năm Zd đạt giá trị cực đại 
2,12 (cm/năm) ở tuổi 2, sau đó giảm dần và ở tuổi 7 lượng tăng trưởng thường xuyên 
Zd đạt 1,00 cm/năm. Từ tuổi 8 đến tuổi 25, lượng tăng trưởng thường xuyên Zd giảm 
từ 0,9058 cm/năm đến 0,3189 cm/năm, lượng tăng trưởng thường xuyên Zd từ tuổi 8 
- 25 bình quân là 0,518 cm/năm. Lượng tăng trưởng bình quân chung ∆d đạt giá trị 
cực đại ở tuổi 3 là 1,77 cm/năm, sau đó giảm dần từ tuổi 4 đến tuổi 25. 
Ở cấp đất III, lượng tăng trưởng thường xuyên Zd đạt giá trị cực đại 1,4725 
(cm/năm) ở tuổi 3, sau đó giảm dần và ở tuổi 6 lượng tăng trưởng thường xuyên Zd 
đạt 1,0784 cm/năm. Từ tuổi 7 đến tuổi 25, lượng tăng trưởng thường xuyên Zd giảm 
từ 0,9963 - 0,4059 cm/năm, lượng tăng trưởng thường xuyên Zd từ tuổi 7 - 25 bình 
quân đạt 0,623 cm/năm. Lượng tăng trưởng bình quân chung ∆d đạt giá trị cực đại là 
1,2503 cm/năm ở tuổi 4, sau đó giảm dần từ tuổi 5 đến tuổi 25. 
Như vậy, lượng tăng trưởng thường xuyên Zd và lượng tăng trưởng bình quân 
chung ∆d ở cấp đất II luôn lớn hơn cấp đất III. Thời điểm đạt được ZDMax và ∆DMax 
ở hai cấp đất có sự khác nhau về thời gian và được trình bày ở hình 4.9 - 4.10. 
Hình 4.9 - Biến đổi Zd và ∆d trên cấp đất II 
Hình 4.10 - Biến đổi Zd và ∆d trên cấp đất III 
0
0.5
1
1.5
2
2.5
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 Tuổi (A)
D1,3 (cm)
Zd
∆d
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 Tuổi (A)
D1,3 (cm)
Zd
∆d
 83 
Căn cứ vào quy trình khảo sát cho thấy, suất trăng trưởng PD% biến đổi theo 
quy luật tuổi càng tăng suất tăng trưởng càng giảm. Phương trình suất tăng trường 
được suy diễn từ phương trình sinh trưởng là PY =100.
𝑌′
𝑌
= 100. 𝑐. 𝑏. 𝐴−𝑐−1. Kết quả 
tìm được hàm tương ứng cho từng cấp đất như sau: 
PD(II) = 100*48,126*3,571*A^(-48,126 -1) 
PD(III) = 100*79,864*4,621*A^(-79,864-1) 
Ly Meng Seang (2009) [67] khi nghiên cứu cây Tếch ở tỉnh Kampong Cham - 
Campuchia cho thấy, trên cấp đất II lượng tăng trưởng thường xuyên hàng năm Zd 
và lượng tăng trưởng bình quân năm ∆d đạt giá trị là 1,65 cm/năm và 2,13 cm/năm 
ở tuổi 2. Tương tự, suất tăng trưởng Pd% đạt khá cao ở tuổi 2 (38,7%), sau đó giảm 
còn 8,4% ở tuổi 8 và 3,4% ở tuổi 18. Từ đó tác giả đi đến kết luận, sinh trưởng và 
tăng trưởng đường kính của rừng trồng Tếch tại Campuchia đạt giá trị cực đại trước 
tuổi 8, sau đó giảm dần. Kết quả này cũng phù hợp với những nghiên cứu của các 
tác giả Nguyễn Văn Thêm (2002) [40] và Mạc Văn Chăm (2005) [3] khi nghiên cứu 
về rừng trồng Tếch ở miền Đông Nam Bộ (Việt Nam). So sánh với kết quả nghiên 
cứu của các tác giả trên cho thấy, kết quả nghiên cứu về sinh trưởng, tăng trưởng 
đường kính của rừng trồng Tếch tại Sơn La cũng không nằm ngoài quy luật trên. 
4.4.3. Nghiên cứu sinh trưởng, tăng trưởng chiều cao 
4.4.3.1. Sinh trưởng chiều cao 
Tương tự như sinh trưởng đường kính, để làm rõ quá trình sinh trưởng chiều 
cao trước hết cần xây dựng mô hình biểu diễn mối quan hệ giữa H với tuổi cây (A, 
năm). Sau đó giải tích mô hình dự đoán tăng trưởng thường xuyên hàng năm (Zh, 
m/năm), lượng tăng trưởng bình quân chung (∆h, cm/năm) và suất tăng trưởng hàng 
năm (Ph,%). Kết quả nghiên cứu cho thấy, giữa chiều cao (H, m) với tuổi cây (A, 
năm) tồn tại mối quan hệ chặt chẽ bằng hàm Schumacher. Phương trình cụ thể cho 
rừng trồng Tếch được trình bày trong bảng 4.22. 
 84 
Bảng 4.22. Mô hình sinh trƣởng 𝐇 rừng trồng Tếch bằng hàm Schumacher 
Cấp 
đất 
Tham số của phƣơng trình 
Phƣơng trình tƣơng quan 
Số 
hiệu PT m b c R2 
II 53,038 5,034 0,508 0,994 H = 53,038*exp(5,034/A**0,508) 4.3 
III 31,731 5,228 0,664 0,992 H = 31,731*exp(-5,228/A**0,664) 4.4 
Từ phương trình (4.3-4.4) xác định được đường cong H cho rừng trồng Tếch 
trên hai cấp đất và những giá trị sinh trưởng 𝐻 từ tuổi 14 trở lên chỉ có ý nghĩa 
tham khảo. Đồ thị mô phỏng quy luật sinh trưởng chiều cao được trình bày trong 
hình 4.11. 
Hình 4.11. Đường cong sinh trưởng 𝑯 trên cấp đất II và III rừng trồng Tếch 
4.4.3.2. Tăng trưởng chiều cao 
Căn cứ vào phương trình (4.3-4.4) tính lượng tăng trưởng thường xuyên và 
tăng trưởng bình quân chiều cao Zh, ∆h. Khi giải phương trình (4.3-4.4), xác định 
được những đại lượng như sau: 
- Ở cấp đất II: Zh= 53,038*5,034*0,508*A^(-0,508-1)*exp(-5,034*A^(-0,508)) 
∆h = (53,038*exp(-5,034/A^0,508))/A 
- Cấp đất III: Zh = 31,731*5,228*0,664*A^(-0,664-1)*exp(-5,228*A^(-0,664)) 
∆h = (31,731*exp(-5,228/A^0,664))/A 
0
5
10
15
20
25
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Tuổi (A)
Hvn (m)
Hbq(II)
Hbq(III)
 85 
Kết quả tăng trưởng chiều cao trên hai cấp đất trình bày trong biểu 4.23. 
Bảng 4.23. Sinh trƣởng và tăng trƣởng chiều cao rừng trồng Tếch 
Cấp đất II Cấp đất III 
A 𝐇 (m) 
Zh 
(m/năm) 
∆h 
(m/năm) 
Ph% A 𝐇 (m) 
Zh 
(m/năm) 
∆h 
(m/năm) 
Ph% 
1 0,72 0,88 0,35 1 1 0,66 0,59 0,17 1 
2 1,93 1,38 0,77 77,56 2 1,57 1,28 0,59 85,47 
3 2,82 1,45* 0,99 48,27 3 2,5 1,42* 0,85 54,11 
4 4,12 1,39 1,10 32,41 4 3,65 1,37 0,99 35,49 
5 5,37 1,30 1,15 23,42 5 4,88 1,26 1,05 24,93 
6 6,95 1,20 1,17* 17,85 6 6,27 1,14 1,06 18,51 
7 8,13 1,11 1,16 14,15 7 7,66 1,03 1,08* 14,34 
8 9,32 1,02 1,15 11,56 8 8,71 0,93 1,07 11,47 
9 10,44 0,95 1,13 9,67 9 9,75 0,84 1,05 9,41 
10 11,51 0,88 1,11 8,23 10 10,64 0,77 1,02 7,88 
11 12,29 0,82 1,09 7,12 11 11,12 0,70 1,00 6,71 
12 12,73 0,77 1,06 6,24 12 11,59 0,65 0,97 5,80 
13 12,92 0,72 1,04 5,52 13 11,7 0,60 0,94 5,06 
14 13,1 0,68 1,01 4,93 14 11,81 0,55 0,92 4,47 
15 13,29 0,64 0,99 4,44 15 11,92 0,51 0,89 3,98 
16 13,48 0,61 0,97 4,02 16 12,03 0,48 0,87 3,57 
17 13,66 0,57 0,95 3,66 17 12,14 0,45 0,84 3,22 
18 13,85 0,54 0,92 3,36 18 12,25 0,42 0,82 2,92 
19 14,04 0,52 0,90 3,09 19 12,36 0,39 0,80 2,67 
20 14,22 0,49 0,88 2,86 20 12,47 0,37 0,78 2,45 
21 14,40 0,47 0,86 2,65 21 12,57 0,35 0,75 2,25 
22 14,59 0,45 0,84 2,47 22 12,68 0,33 0,73 2,08 
23 14,78 0,43 0,82 2,31 23 12,79 0,31 0,71 1,93 
24 14,96 0,41 0,81 2,16 24 12,90 0,29 0,70 1,79 
25 15,15 0,39 0,79 2,03 25 13,01 0,28 0,68 1,67 
 86 
Kết quả bảng 4.23 cho thấy, sinh trưởng chiều cao cũng tăng nhanh trong 7 
năm đầu, sinh trưởng chiều cao tăng trưởng mạnh từ tuổi 3 - 7 sau đó tăng trưởng 
chậm dần. 
Ở cấp đất II, lượng tăng trưởng thường xuyên Zh đạt giá trị cực đại 1,45 
m/năm ở tuổi 3, sau đó giảm dần và ở tuổi 8 lượng tăng trưởng thường xuyên Zh đạt 
1,02 m/năm. Từ tuổi 9 đến tuổi 25, lượng tăng trưởng thường xuyên Zh giảm từ 0,95 
- 0,39 m/năm. Lượng tăng trưởng thường xuyên Zh bình quân từ tuổi 9 - 25 là 0,608 
m/năm. Lượng tăng trưởng bình quân chung ∆h đạt giá trị cực đại ở tuổi 6 là 1,17 
m/năm, sau đó giảm dần và ở tuổi 14 lượng tăng trưởng bình quân chung ∆h đạt 
1,01 m/năm, từ tuổi 15 đến tuổi 25 lượng tăng trưởng bình quân chung ∆h giảm từ 
0,99 - 0,79 m/năm. 
Trên cấp đất III, tương tự lượng tăng trưởng thường xuyên Zh đạt giá trị cực 
đại 1,42 m/năm ở tuổi 3, sau đó giảm dần và ở tuổi 7 lượng tăng trưởng thường 
xuyên Zh đạt 1,03 m/năm. Từ tuổi 8 đến tuổi 25, lượng tăng trưởng thường xuyên 
Zh giảm từ 0,93 - 0,28 m/năm. Lượng tăng trưởng thường xuyên Zh từ tuổi 8 - 25 
bình quân đạt 0,512 m/năm. Lượng tăng trưởng bình quân chung ∆h đạt giá trị cực 
đại ở tuổi 7 là 1,08 m/năm, sau đó giảm dần và ở tuổi 11 tăng trưởng bình quân 
chung ∆h đạt 1,00 m/năm, từ tuổi 12 đến tuổi 25 lượng tăng trưởng bình quân chung 
∆h giảm từ 0,97 - 0,68 m/năm. Như vậy, lượng tăng trưởng thường xuyên Zh và 
lượng tăng trưởng bình quân chung ∆h ở cấp đất II luôn lớn hơn cấp đất III. Thời 
điểm đạt được ZHMax và ∆HMax ở hai cấp đất có sự khác nhau về thời gian và được 
trình bày ở hình 4.12 - 4.13. 
Hình 4.12. Biến đổi Zh và ∆h trên cấp đất II 
Hình 4.13. Biến đổi Zh và ∆h trên cấp đất III 
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 Tuổi (A)
Hvn (m)
Zh
∆h
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 Tuổi (A)
Hvn (m)
Zh
∆h
 87 
Suất trăng trưởng Ph% biến đổi theo quy luật tuổi càng tăng suất tăng trưởng 
càng giảm. Tương tự như với đường kính, suất tăng trưởng chiều cao cũng phù hợp 
với phương trình PY =100.
𝑌′
𝑌
= 100. 𝑐. 𝑏. 𝐴−𝑐−1. Kết quả tìm được hàm tương ứng 
cho từng cấp đất như sau: 
Ph(II) = 100*53,038*5,034*A^(-53,038-1) 
Ph(III) = 100*31,731*5,228*A^(-31,731-1) 
4.4.4. Nghiên cứu sinh trưởng, tăng trưởng thể tích 
4.4.4.1. Sinh trưởng thể tích 
Tương tự như sinh trưởng đường kính và chiều cao, sinh trưởng thể tích cũng 
được mô hình hóa bằng hàm Schumacher. Kết quả được trình bày trong bảng 4.24. 
Bảng 4.24. Mô hình sinh trƣởng 𝐕 rừng trồng Tếch bằng hàm Schumacher 
Cấp 
đất 
Tham số của phƣơng trình 
Phƣơng trình tƣơng quan 
Số hiệu 
PT m b c R
2
II 2,464 10,84 0,509 0,999 V = 2,464*exp(-10,84/A**0,509) 4.5 
III 1,945 10,43 0,596 0,999 V = 1,945*exp(-10,43/A**0,596) 4.6 
Từ phương trình (4.5-4.6) xác định đường cong sinh trưởng thể tích cho rừng 
trồng Tếch trên hai cấp đất, và những giá trị sinh trưởng 𝑉 từ tuổi 14 trở lên chỉ có 
ý nghĩa tham khảo. Kết quả được mô phỏng ở hình 4.14. 
Hình 4.14. Đường cong sinh trưởng 𝑉 trên cấp đất II và III rừng trồng Tếch 
0.0000
0.0500
0.1000
0.1500
0.2000
0.2500
0.3000
0.3500
0.4000
0.4500
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 Tuổi (A)
V (m3)
Vbq (II)
Vbq (III)
 88 
4.4.4.2. Tăng trưởng thể tích 
Căn cứ vào phương trình (4.5-4.6) tính được lượng tăng trưởng thường xuyên 
và tăng trưởng định kỳ của thể tích ZV, ∆V. Khi giải phương trình (4.5-4.6), xác định 
được những đại lượng như sau: 
- Ở cấp đất II: ZV =2,464*10,846*0,509*A^(-0,509-1)*exp(-10,846*A^(-0,509)) 
∆V = (2,464*exp(-10,846/A^0,509))/A 
- Cấp đất III: ZV = 1,945*10,433*0,596*A^(-0,5096-1)*exp(-10,433*A^(-0,596)) 
∆V = (1,945*exp(10,433/A^0,596))/A 
Kết quả tính tăng trưởng thể tích ở hai cấp đất trình bày trong bảng 4.25. 
Bảng 4.25. Sinh trƣởng và tăng trƣởng thể tích rừng trồng Tếch 
Cấp đất II Cấp đất III 
A 
𝐕 
(m
3
) 
Zv 
(m
3/năm) 
∆V 
(m
3/năm) 
PV% A 
𝐕 
(m
3
) 
Zv 
(m
3/năm) 
∆V 
(m
3/năm) 
PV% 
2 0,0013 0,0024 0,00053