Luận án Nghiên cứu và phát triển hệ thống năng lượng điện mặt trời

Trang 1

Trang 2

Trang 3

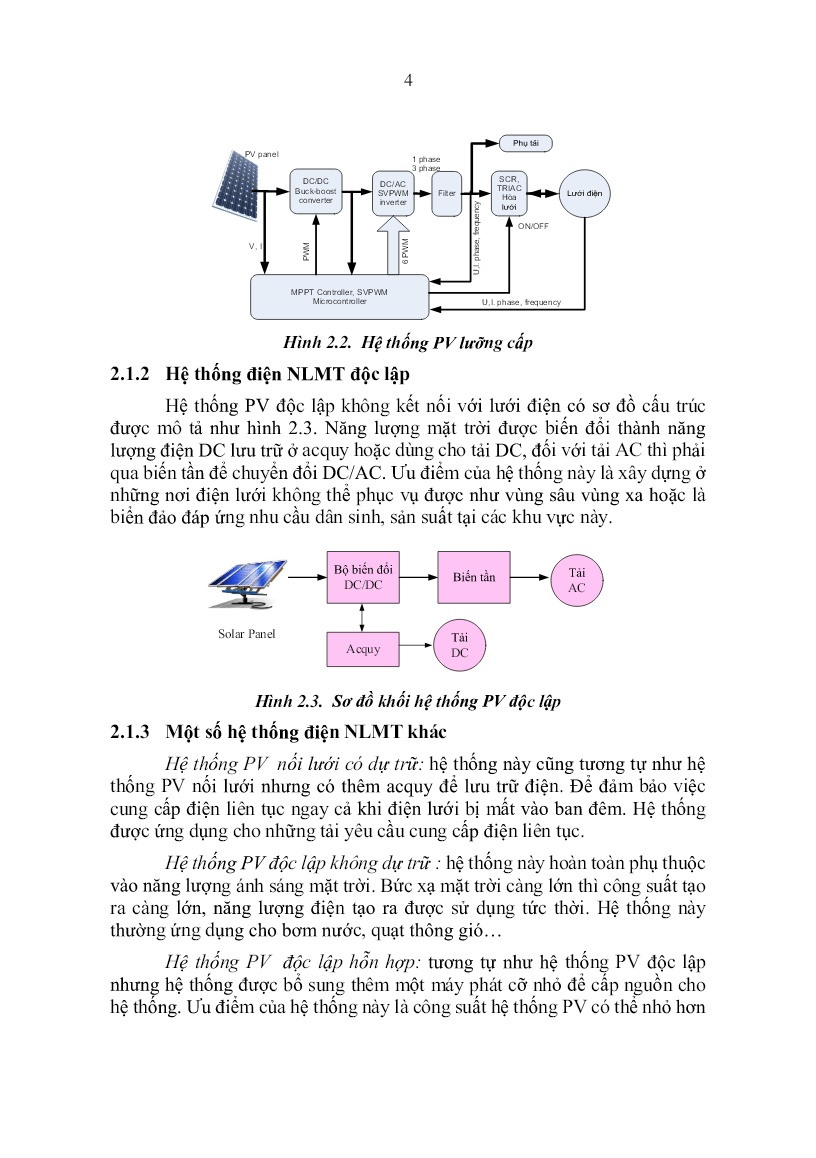
Trang 4

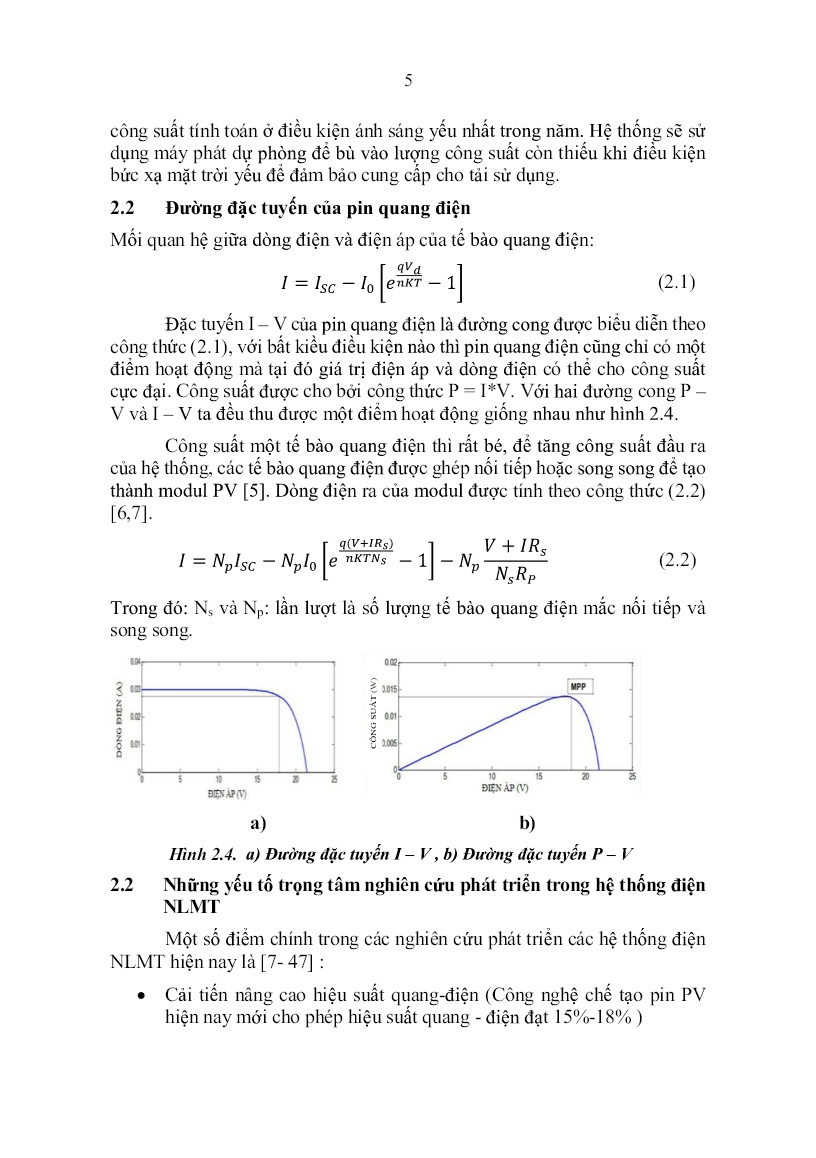
Trang 5
Trang 6
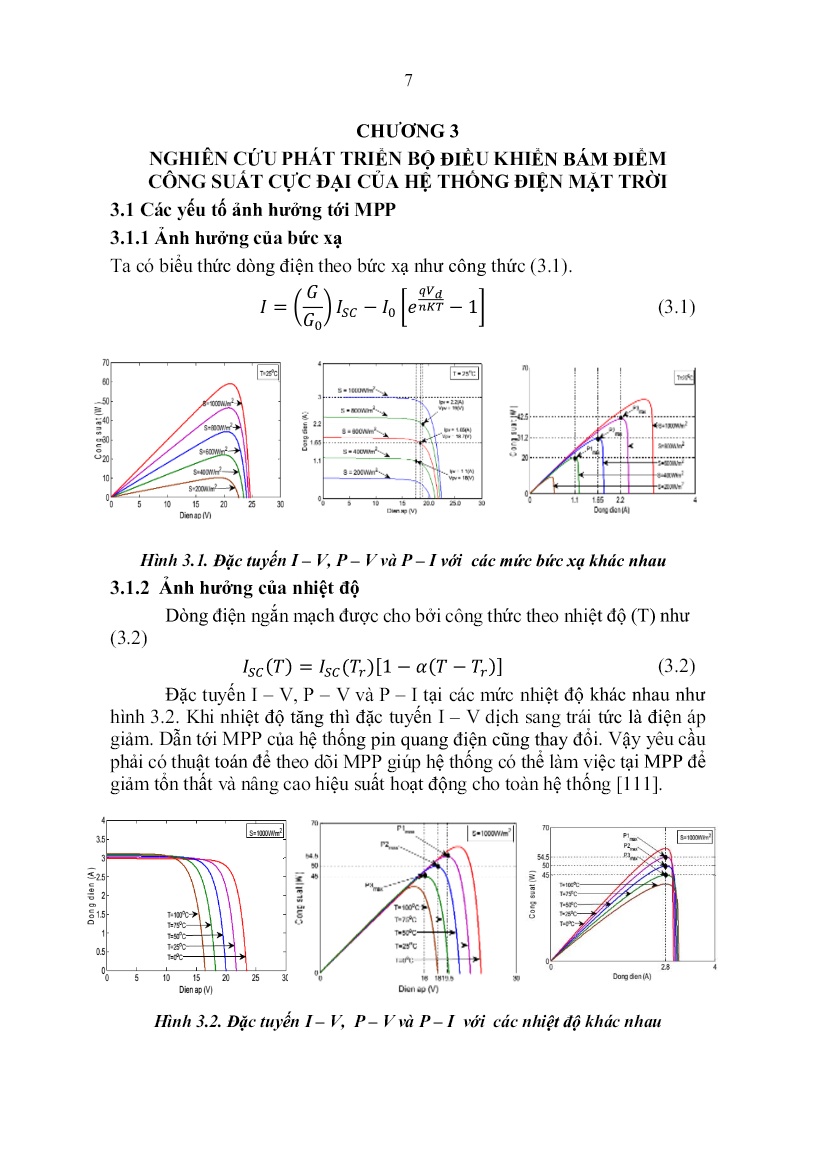
Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Luận án Nghiên cứu và phát triển hệ thống năng lượng điện mặt trời", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Luận án Nghiên cứu và phát triển hệ thống năng lượng điện mặt trời

I-V, P-V khi có bóng râm 3.2 Tìm điểm công suất cực đại Một thành phần quan trọng trong hệ thống PV là MPPT, thành phần này giúp hệ thống PV phát được công suất ngõ ra của hệ thống cực đại, giảm tổn thất công suất và giải quyết bài toán kinh tế cho hệ thống PV. Nó như là một thiết bị công suất liên kết hệ pin quang điện với tải, điều khiển điểm hoạt động của hệ pin quang điện để thu được công suất cực đại từ hệ pin quang điện với điều kiện môi trường thay đổi như nhiệt độ, bức xạ, bóng râm vì thế hiệu suất hệ thống được cải thiện. 3.3 Nghiên cứu phát triển thuật toán độ dẫn gia tăng trong điều khiển bám điểm công suất cực đại 3.3.1 Theo dõi MPP bằng thuật toán INC truyền thống Sơ đồ thuật toán INC như hình 3.4 [5]: Hình 3.4. Sơ đồ thuật toán INC 9 Nếu coi D là một biến điều khiển thì lưu đồ thuật toán INC truyền thống được viết lại như hình 3.5. Start Read V(k), I(k) dV = V(k) - V(k-1); dI = I(k) - I(k-1) dP = V(k)*I(k) - V(k-1)*I(k-1) D D(k) = D Dmax No Yes dV = 0 Yes Yes D(k) = D(k-1) dI/dV = - I/V dI = 0 D(k) = D(k-1) No No Yes Yes dI/dV > - I/V dI > 0 D(k) = D(k-1) - D D(k) D(k) = D(k-1) + D D(k) No No D(k) = D(k-1) + D D(k) D(k) = D(k-1) - D D(k) V(k-1) = V(k); I(k-1) = I(k) Return Hình 3.5. Lưu đồ thuật toán INC với biến D cố định Trong lưu đồ thuật toán hình 3.5 kích thước bước được cố định. Sự cố định về kích thước bước nhảy cố định ảnh hưởng đến hiệu quả điều khiển MPPT của thuật toán INC. Nếu kích thước bước lớn thì hệ thống nhanh đạt tới trạng thái MPP, nhưng độ dao động quanh điểm MPP lại lớn, làm giảm hiệu suất của MPPT. Và ngược lại, nếu kích thước bước nhỏ, thì thời gian để hệ thống PV đạt tới trạng thái MPP lại lâu. Sự hạn chế này được khắc phục bằng việc phát triển thuật toán INC với kích thước bước nhảy tự điều chỉnh sẽ được trình bày ở phần tiếp theo. 3.3.2 Phát triển thuật toán INC nhằm đạt MPP nhanh Phương pháp xác định kích thước bước nhảy tự điều chỉnh sẽ được xác định như sau: 푃 ( ) = ( − 1) ± ∗ | | (3.3) − Trong đó: N là tham số, tham số này sẽ quyết định kích thước bước trong thuật toán INC. Sơ đồ lưu đồ của thuật toán MPPT INC có bước thay đổi được trình bày trong hình 3.6. 10 Start Read V(k), I(k) dV = V(k) - V(k-1); dI = I(k) - I(k-1) dP = V(k)*I(k) - V(k-1)*I(k-1) DD(k) = N*abs(dP/(dV-dI)) No Yes dV = 0 Yes Yes D(k) = D(k-1) dI/dV = - I/V dI = 0 D(k) = D(k-1) No No Yes Yes dI/dV > - I/V dI > 0 D(k) = D(k-1) - DD(k) D(k) = D(k-1) + DD(k) No No D(k) = D(k-1) + DD(k) D(k) = D(k-1) - DD(k) V(k-1) = V(k); I(k-1) = I(k) Return Hình 3.6. Lưu đồ thuật toán INC với kích thước bước nhảy thay đổi nhằm mục đích hội tụ nhanh 3.3.3 Phát triển thuật toán INC nhằm giảm dao động quanh MPP Khi hệ thống ở trạng thái xác lập, các giá trị biến thiên công suất không lớn, thì một giá trị bước nhảy càng nhỏ sẽ càng giảm độ giao động, giảm tổn thất công suất cho hệ thống. Trong thuật toán đề xuất này, đề tài cũng áp dụng một giá trị bước nhảy có độ lớn giảm dần về giá trị 0, để giảm độ giao động của công suất khi đạt MPP. ∆ | 푃| ∆ = −1 (3.4) 훼 Với điều kiện như biểu thức (3.4), bước nhảy tiếp theo sẽ được xác định dựa vào độ biến đổi của bước nhảy phía trước, và nếu công suất thay đổi nhỏ, thì giá trị bước nhảy sẽ giảm dần với một hệ số chia α, và giá trị α này thường được chọn là 2. 11 Start Read V(k), I(k) dV = V(k) - V(k-1); dI = I(k) - I(k-1) dP = V(k)*I(k) - V(k-1)*I(k-1) No Yes D D(k) = D D(k-1)/2 dP D D(k) = N*abs(dP/(dV-dI)) Yes No Yes dV = 0 Yes Yes D(k) = D(k-1) dI/dV = - I/V dI = 0 D(k) = D(k-1) No No Yes Yes dI/dV > - I/V dI > 0 D(k) = D(k-1) - D D(k) D(k) = D(k-1) + D D(k) No No D(k) = D(k-1) + D D(k) D(k) = D(k-1) - D D(k) V(k-1) = V(k); I(k-1) = I(k) Return Hình 3.7. Lưu đồ thuật toán INC với kích thước bước nhảy thay đổi nhằm mục đích giảm dao động tại MPP 3.4 Nghiên cứu phát triển thuật toán tối ưu bầy đàn trong điều khiển bám điểm công suất cực đại 3.4.1 Thuật toán tối ưu bầy đàn (PSO) PSO (Particle Swarm Optimization) là một trong những kỹ thuật tính toán tiến hóa được đề xuất bởi Eberhart và Kennedy vào năm 1995 [48,49]. PSO được phỏng theo hành vi xã hội và hợp tác của nhiều loài khác nhau để đáp ứng nhu cầu tìm kiếm thức ăn của chúng trong không gian đa chiều. Khái niệm về PSO nguyên thể (được gọi là PSO) được thể hiện bằng hai phương trình toán học dưới đây [65]: 12 k 1 k k k k k Vij, wV ij , c 1 r 1()() Pbest ijij , X , c 2 r 2 Gbest jij X , (3.5) k 11 k k XXVi,,, j i j i j (3.6) Sơ đồ thuật toán của PSO được thể hiện trong Hình 3.8. Đặt thông số PSO Khởi tạo vị trí và vận tốc ban đầu của mỗi cá thể Tính toán giá trị hàm mục tiêu của mỗi cá thể Đánh giá hàm mục tiêu của mỗi cá thể, chọn Pbest và Gbest Đặt số lần lặp k =1 Cập nhật giá trị vận tốc và vị trí của mỗi cá thể Đánh giá hàm mục tiêu của mỗi cá thể và cập nhật Pbest, Gbest Đúng k = k+1 Nếu k <= Maxite ? Sai In giá trị tối ưu của đầu ra, Gbest Hình 3.8 Sơ đồ thuật toán của PSO 3.4.2 Phát triển thuật toán tối ưu bầy đàn 3.4.2.1 Thuật toán tối ưu bầy đàn vi phân (DPSO) DPSO là phát triển của thuật toán tối ưu bầy đàn (PSO), trong đó các cá thể có khả năng thoát khỏi tối ưu cục bộ, để tìm giải pháp tối ưu hóa tốt hơn trong không gian tìm kiếm. 13 Thuật toán DPSO khắc phục nhược điểm của PSO bằng cách cập nhật thêm tốc độ của một cá thể ngẫu nhiên được chọn trong bầy đàn. Sự khác biệt tỷ lệ ngẫu nhiên giữa bản thân cá thể đang xét và và cá thể được chọn mới, được thể hiện trong phương trình vận tốc. Về mặt toán học, thuật toán DPSO có thể được trình bày như sau: Vk 1 wV k c r()()() Pbest k X k c r Gbest k X k c r X k X k pq,,,,,, pq11 pqpq 2 2 qpq 3 3 lq, pq (3.11) k 11 k k XXVp,,, q p q p q (3.12) Chú ý rằng l đại diện cho cá thể chuyên gia tương ứng với cá thể mục tiêu p. Trong phương trình này, l thay đổi từ 1 đến N nhưng l ≠ p. Hình 3.9 thể hiện cơ chế tìm kiếm của DPSO được đề xuất trong không gian tìm kiếm đa chiều. k+1 Xp k Vp k+1 Vp Gbestk Gbest Vp k Pbestp X k Pbest p Vp Diff Vp Hình 3.9 Cơ chế tìm kiểm của DPSO trong không gian đa chiều k Trong hình 3.9, Pbestp ,q đại diện cho thành phần thứ q cá thể tốt k nhất của cá thể thứ p, trong khi Gbestq đại diện cho thành phần thứ q của cá thể tốt nhất cho đến lần lặp k. Từ hình 3.9 có thể thấy rằng DPSO được đề xuất được thực hiện Diff bằng cách thêm một đặc trưng mới (Vp ) trong phương trình vận tốc, do đó điểm công suất cực đại có thể thu được sớm hơn nhiều so với trường hợp sử dụng PSO cổ điển. Hơn nữa, tính năng bổ sung này cho phép các cá thể thoát khỏi tối ưu cục bộ để tìm kiếm một giải pháp tốt hơn trong không gian tìm kiếm. Thuật toán MPPT dựa trên DPSO (MPPT – DPSO) Như đã đề cập ở chương 2, đặc tính tế bào quang điện là phi tuyến tính, có công suất đầu ra thay đổi theo sự biến đổi của bức xạ ánh sáng và nhiệt độ, do đó làm giảm hiệu quả hoạt động của tấm pin mặt trời (PV). Ngoài ra, hiệu quả của các mô-đun quang điện này không được đạt yêu cầu, do đó đòi hỏi sự hỗ trợ của các thuật toán thông minh để khắc phục vấn đề này. 14 Trong luận án này, một mô hình sử dụng thuật toán MPPT dựa trên DPSO được đề xuất để nâng cao hiệu quả hoạt động của PV. Lưu đồ thuật toán của MPPT - DPSO được thể hiện trên hình 3.10: Chọn giá trị w, c1, c2 , c3, n Khởi tạo vị trí và vận tốc ban đầu của mỗi cá thể d=d0; v=0.1*d0 Xác định V(i), I(i). Tính toán giá trị hàm mục tiêu của mỗi cá thể: P(i)=V(i)*I(i) Đánh giá hàm mục tiêu của mỗi cá thể, chọn Pbest và Gbest Đặt số lần lặp k =1 Cập nhật giá trị vận tốc và vị trí của mỗi cá thể Đánh giá hàm mục tiêu của mỗi cá thể và cập nhật Pbest, Gbest Đúng k = k+1 Nếu k <= Maxite ? Sai In giá trị tối ưu của chu kỳ xung, Gbest Hình 3.10. Sơ đồ thuật toán của MPPT - DPSO 3.4.2.2 Thuật toán tối ưu bầy đàn nhiễu loạn (PPSO) Thuật toán PPSO cũng là một phát triển của thuật toán PSO nó làm việc dựa trên nguyên tắc sau: bất cứ khi nào các cá thể bị hội tụ vào vùng cực đại cục bộ vectơ vận tốc của mỗi cá thể cần được thực hiện nhiễu loạn. Thông thường, tình huống này xảy ra khi giải pháp tối ưu (Gbest của bầy đàn) không được cải thiện sau một số lần lặp nhất định, chẳng hạn như sau một giá trị sai 15 lệch cho phép (dung sai) hoặc khi đạt đến một tiêu chí dừng (được quy định trước và phải nhỏ hơn số lần lặp tối đa). Nhiễu loạn là hiện tượng vectơ vận tốc của mỗi cá thể cần được thiết lập lại, để các cá thể có thể thoát ra khỏi cực đại cục bộ. Về mặt toán học, các khái niệm nhiễu loạn vận tốc cho mỗi cá thể có thể được biểu diễn như sau: kk 1 Vp,, q pbest p q (3.13) Ngoài ra, giới hạn dung sai cần được điều chỉnh, để các cá thể có khả năng tìm kiếm các cơ hội khác tối ưu hơn trong không gian với một số lần lặp tối thiểu nhất định. Bên cạnh đó, sự nhiễu loạn vận tốc có thể được thực hiện với một số lần nhất định. Nói cách khác, sự nhiễu loạn trong vectơ vận tốc của mỗi cá thể cho phép các cá thể tiếp tục khám phá không gian tìm kiếm để thoát khỏi cực đại cục bộ. Một mô hình mô tả điển hình của mỗi cá thể tương ứng với chiều dài tăng dần của mũi tên của các cá thể bị nhiễu loạn vận tốc (PP) được thể hiện trong Hình 3.11. IP: Initialized Particle PP: Perturbed Particle LCP: Locally Converged Particle Arrow: Represents direction of move Length of arrow: Values of velocity IP4 PP4 Local optimum IP5 PP5 PP3 Global optimum IP4 LCP4 IP1 LCP3 LCP5 LCP2 LCP1 IP2 PP3 IP3 PP1 Hình 3.11 Cơ chế tìm kiếm của PPSO trong không gian đa chiều Thuật toán MPPT dựa trên PPSO ( MPPT-PPSO) Lưu đồ thuật toán của phương pháp MPPT-PPSO được đề xuất như Hình 3.12. Đầu tiên, giá trị chu kỳ xung D của bộ chuyển đổi DC/DC được chọn làm vị trí của cá thể trong không gian tìm kiếm. Trong khi đó, công suất đầu ra của dãy PV được định nghĩa là giá trị hàm mục tiêu. Cần lưu ý rằng số lượng của các cá thể nên được chọn là số lượng các mô đun kết nối nối tiếp trong dãy PV. Tiếp theo, thuật toán PPSO sẽ bắt đầu quá trình tối ưu hóa từ một giá trị ban đầu ngẫu nhiên được chọn trong phạm vi sau: k Di = [D1, D2, D3, DN] 16 Đặt giá trị w , c1 , c2,c3 , n Khởi tạo vị trí và vận tốc ban đầu của mỗi cá thể d=d0; v=0.1*d0 Xác định V(i), I(i). Tính toán giá trị hàm mục tiêu của mỗi cá thể: P(i)=V(i)*I(i) Đánh giá hàm mục tiêu của mỗi cá thể, chọn Pbest và Gbest Đặt số lần lặp k =1 Cập nhật giá trị vận tốc và vị trí của mỗi cá thể Đánh giá hàm mục tiêu của mỗi cá thể và cập nhật Pbest, Gbest Yes If tol<tol_max tol=1 No k k+1 tol = Fb - Fb1 V=Pbest Đúng k = k+1 If k <= Maxite ? Sai In giá trị tối ưu của chu kỳ xung, Gbest Hình 3.12 Lưu đồ thuật toán MPPT-PPSO Trong đó N là số cá thể và k là số lần lặp. Nói cách khác, các cá thể được khởi tạo bởi các vị trí ngẫu nhiên trong không gian tìm kiếm [Dmin, Dmax]. Dmax và Dmin lần lượt là chu kỳ xung tối đa và tối thiểu của bộ chuyển đổi DC/DC được sử dụng trong nghiên cứu. Sau đó, bộ điều khiển kỹ thuật số gửi tín hiệu điều khiển PWM theo chu kỳ xung (tín hiệu này đại diện cho 17 vị trí của cá thể thứ i), điện áp và dòng điện đầu ra của dãy pin, VPV và IPV được xác định, từ đó tính được công suất đầu ra của dãy pin (giá trị hàm mục tiêu), theo công thức: PPV = VPV*IPV. Giá trị hàm mục tiêu của từng cá thể k k được đánh giá theo công thức: Fp = f(Xp ) ∀p, để tìm chỉ số cá thể tốt nhất b. Cuối cùng, thuật toán PPSO cập nhật Pbest, Gbest cho đến khi đạt được giá trị tối ưu của chu kỳ xung, được gọi là Gbest. Cần lưu ý rằng bất cứ khi nào k k + 1 tol <tol_max thì V = Pbest và tol = 1, nếu sai tol = Fb - Fb1 . 3.5 Kết luận chương 3 Trong hệ thống PV người ta luôn mong muốn cho dù ở bất kỳ điều kiện thời tiết như thế nào thì dòng công suất phát từ dàn PV tới tải luôn là cực đại, đó là mục tiêu của bài toán điều khiển MPPT. Chương 3 tác giả nghiên cứu các thuật toán điều khiển công suất cực đại thông dụng và đưa ra các cải tiến phát triển cho thuật toán để áp dụng trong điều khiển MPPT của hệ thống PV làm cho hệ thống hoạt động hiệu suất tốt hơn. Chương 3 tác giả giới thiệu một số thuật toán cho bộ điều khiển MPPT và nghiên cứu thuật toán INC và đưa ra các cải tiến phát triển cho thuật toán INC làm cho hệ thống đạt điểm công suất cực đại nhanh hơn, dao động quanh điểm công suất cực đại hẹp và ít hơn, giảm thiểu được hao tổn công suất phát do dao động quanh điểm công suất cực đại. Trong chương 3 này tác giả cũng chú trọng nghiên cứu thuật toán PSO áp dụng trong điều khiển MPPT và đã đề xuất ra các thuật toán mới bằng cách phát triển dựa trên thuật toán PSO cổ điển đó là thuật toán DPSO và thuật toán PPSO để cải thiện hiệu quả hoạt động của hệ thống PV. CHƯƠNG 4 MÔ PHỎNG KIỂM CHỨNG CÁC THUẬT TOÁN MPPT PHÁT TRIỂN CHO HỆ THỐNG NĂNG LƯỢNG ĐIỆN MẶT TRỜI 4.1. Kết quả mô phỏng thuật toán INC các phát triển của thuật toán INC 4.1.1. Sơ đồ mô phỏng Hình 4.1. Sơ đồ mô phỏng thuật toán INC 18 4.1.2 Kết quả mô phỏng 4.1.2.2 Thuật toán phát triển INC nhằm đạt MPP nhanh Tác giả tiến hành mô phỏng theo lý thuyết đã đề xuất thì thu được kết quả các đáp ứng của hệ thống PV so với trường hợp INC truyền thống như hình 4.2. CURRENT Traditional I 25 Variable I 20 15 I(A) 10 5 0 0 2 4 6 8 10 12 14 Time(s) a) So sánh đáp ứng dòng điện VOLTAGE 400 Traditional V 350 Variable V 300 250 200 V(V) 150 100 50 0 0 2 4 6 8 10 12 14 Time(s) b) So sánh đáp ứng điện áp POWER 8000 7000 6000 5000 4000 P(W) 3000 2000 Theory P 1000 Traditional P Variable P 0 0 2 4 6 8 10 12 14 Time(s) c) So sánh đáp ứng công suất Hình 4.2. So sánh các đáp ứng của thuật toán INC truyền thống và bước nhảy thay đổi DUTY CYCLE 0.6 Traditional D 0.55 Variable D 0.5 0.45 0.4 0.35 Duty 0.3 0.25 0.2 0.15 0.1 0 0.5 1 1.5 2 2.5 3 3.5 4 Time(s) Hình 4.3 Đáp ứng D của INC truyền thống và bước nhảy thay đổi lúc khởi động 19 POWER 7000 6000 5000 4000 P(W) 3000 2000 Theory P 1000 Traditional P Variable P 0 0 0.5 1 1.5 2 2.5 3 3.5 4 Time(s) Hình 4.4 Đáp ứng công suất của INC truyền thống và bước nhảy thay đổi lúc khởi động POWER 7800 7600 7400 7200 7000 6800 P(W) 6600 6400 6200 Theory P 6000 Traditional P Variable P 5800 4 4.05 4.1 4.15 4.2 4.25 4.3 4.35 4.4 4.45 4.5 Time(s) Hình 4.5 Đáp ứng công suất của INC truyền thống và bước nhảy thay đổi lúc bức xạ thay đổi từ 700W/m2 lên 900W/m2. Qua mô phỏng ta dễ dàng quan sát được tốc độ đạt MPP lúc bắt đầu hoạt động của INC bước nhảy thay đổi nhanh hơn INC truyền thống rất nhiều được thể hiện ở hình 4.4. Ngay cả trong trường hợp bức xạ thay đổi từ G = 700W/m2 lên G = 900W/m2 thuật toán INC bước nhảy thay đổi bám điểm công suất tốt hơn, được thể hiện ở hình 4.5, qua đây có thể thấy INC bước nhảy thay đổi dao động quanh MPP nhẹ hơn so với INC truyền thống. 4.1.2.3 Thuật toán phát triển INC nhằm giảm dao động tại MPP Kết quả thu được từ mô phỏng phần mềm Matlab như hình 4.6 ta thấy được phương án đề xuất này có tốc độ hội tụ nhanh và giảm dao động tại MPP đáng kể. CURRENT Traditional I 25 Modify Variable I 20 15 I(A) 10 5 0 0 2 4 6 8 10 12 14 Time(s) a) So sánh đáp ứng dòng điện 20 VOLTAGE 400 Traditional V 350 Modify Variable V 300 250 200 V(V) 150 100 50 0 0 2 4 6 8 10 12 14 Time(s) b) So sánh đáp ứng điện áp POWER 8000 Theory P 7000 Modify Variable P 6000 5000 4000 P(W) 3000 2000 1000 0 0 2 4 6 8 10 12 14 16 Time(s) c) So sánh đáp ứng công suất Hình 4.6. So sánh thuật toán INC truyền thống và giảm dao động tại MPP DUTY CYCLE 0.6 Traditional D 0.55 Modify Variable D 0.5 0.45 0.4 0.35 Duty 0.3 0.25 0.2 0.15 0.1 0 0.5 1 1.5 2 2.5 3 3.5 4 Time(s) a) Đáp ứng D quá trình khởi động Time(s) 3.9 3.95 4 4.05 4.1 4.15 4.2 4.25 4.3 4.35 4.4 0.46 0.47 0.48 0.49 0.5 Duty 0.51 0.52 0.53 0.54 Modify Variable D Traditional D 0.55 DUTY CYCLE b) Đáp ứng D ở thời điểm gia tăng bức xạ Hình 4.7. Đồ thị D khi quá độ và tăng bức xạ Từ hình 4.7 a) ta nhận thấy rằng, với một giá trị bước nhảy thay đổi, hệ thống sẽ nhiễu loạn những bước dài hơn, được giới hạn 10%, và càng gần 21 giá trị công suất cực đại, giá trị bước nhảy nhỏ dần và tiến gần đến 0, trong đó giá trị giảm dần α được chọn là 2, có nghĩa là thuật toán sẽ liên tục giảm giá trị bước nhảy cho 2 cho đến khi đạt giá trị gần 0. Việc này cải thiện được độ giao động công suất ở trạng thái xác lập. Để so sánh được hiệu quả giữa các phương pháp, tác giả vẽ lại các đường công suất tại thời điểm khởi động như hình 4.8 a), gia tăng ánh nắng như hình 4.8 b) và hệ thống ổn định hình 4.8 c). POWER 7000 6000 5000 4000 P(W) 3000 2000 Theory P 1000 Traditional P Variable P Modify Variable P 0 0 0.5 1 1.5 2 2.5 3 3.5 4 Time(s) a) Đáp ứng P ở quá trình khởi động POWER 7800 7600 7400 7200 7000 6800 P(W) 6600 6400 6200 Theory P Traditional P 6000 Variable P Modify Variable P 5800 4 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5 Time(s) b) Đáp ứng P ở quá trình thay đổi bức xạ POWER 6860 6840 6820 6800 6780 6760 P(W) 6740 6720 6700 Theory P Traditional P 6680 Variable P Modify Variable P 6660 11 11.2 11.4 11.6 11.8 12 12.2 12.4 12.6 12.8 13 Time(s) c) Đáp ứng P trong quá trình ổn định Hình 4.8 So sánh đáp ứng công suất của 3 thuật toán và lý thuyết Từ những kết quả mô phỏng và so sánh trên, đã chứng minh được rằng 2 thuật toán đề xuất có khả năng cải thiện được hiệu suất của thuật toán INC truyền thống ở các tiêu chí về thời gian đáp ứng, độ dao động tại MPP và tổn thất công suất. Điều này chứng minh sự phù hợp của các thuật toán đề xuất so với thuật toán truyền thống. 22 4.2. Kết quả mô phỏng thuật toán PSO và các phát triển của thuật toán PSO 4.2.1 Kết quả mô phỏng thuật toán MPPT-PSO Dựa vào lưu đồ thuật toán PSO hình 3.8 tác giả mô phỏng được các đáp ứng công suất đầu ra của hệ thống PV và so sánh với trường hợp không có bộ điều khiển MPPT như hình 4.9. Từ đáp ứng đầu ra ta thấy với thuật toán PSO cho kết quả đáp ứng công suất đầu ra không bị giao động như các phương pháp INC hay P&O. Hình 4.9 Đáp ứng đầu ra hệ thống PV với thuật toán PSO 4.2.2 Kết quả mô phỏng thuật toán MPPT-DPSO Trong phần này, tác giả mô phỏng để đánh giá hiệu quả của thuật toán DPSO trong việc dò tìm điểm công suất cực đại của PV. Trước tiên, thuật toán PSO và DPSO được thử nghiệm trên năm vấn đề Benchmark để chứng minh tính hiệu quả của chúng trong việc giải quyết các vấn đề tối ưu hóa phức tạp. Sau đó, các thuật toán tối ưu hóa này được áp dụng để dò tìm điểm công suất cực đại của PV. Hình 4.10 thể hiện thời gian đáp ứng của công suất đầu ra trong điều kiện môi trường không đổi (với năng lượng bức xạ G = 900 W / m2 và nhiệt độ T = 25°C) trong ba trường hợp sau: 1) không có bộ điều khiển MPPT, 2) sử dụng DPSO và 3) các phương pháp truyền thống (P&O and InCond). Hình 4.10. Đáp ứng của công suất đầu ra trong ba trường hợp: không sử dụng MPPT, sử dụng DPSO, P&O và InCond 23 Khả năng dò tìm điểm công suất cực đại của phương pháp được đề xuất tốt hơn thuật toán bầy đàn PSO truyền thống trong việc tối ưu hóa năng lượng của tấm pin mặt trời. Điều này được thể hiện trong hình 4.11 có thể thấy rằng cả hai thuật toán thông minh nh
File đính kèm:
 luan_an_nghien_cuu_va_phat_trien_he_thong_nang_luong_dien_ma.pdf
luan_an_nghien_cuu_va_phat_trien_he_thong_nang_luong_dien_ma.pdf ._Tom tat LATS T.Anh.pdf
._Tom tat LATS T.Anh.pdf ._Tom tat LATS T.Viet.pdf
._Tom tat LATS T.Viet.pdf ._Trang thong tin tom tat LATS T.Anh.pdf
._Trang thong tin tom tat LATS T.Anh.pdf ._trang thong tin tom tat LATS T.Viet.pdf
._trang thong tin tom tat LATS T.Viet.pdf Tom tat LATS T.Anh.pdf
Tom tat LATS T.Anh.pdf Trang thong tin tom tat LATS T.Anh.pdf
Trang thong tin tom tat LATS T.Anh.pdf trang thong tin tom tat LATS T.Viet.pdf
trang thong tin tom tat LATS T.Viet.pdf

