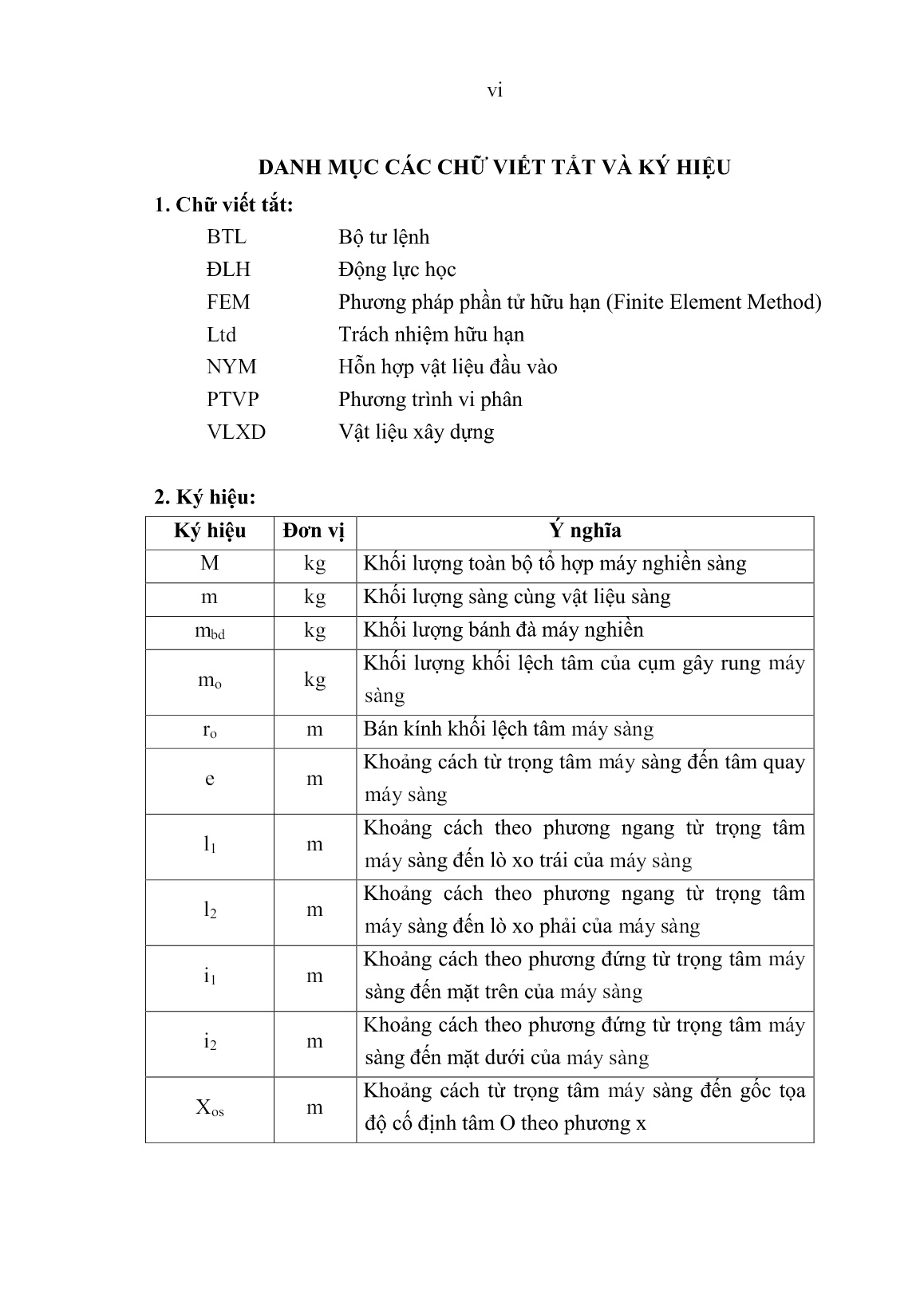
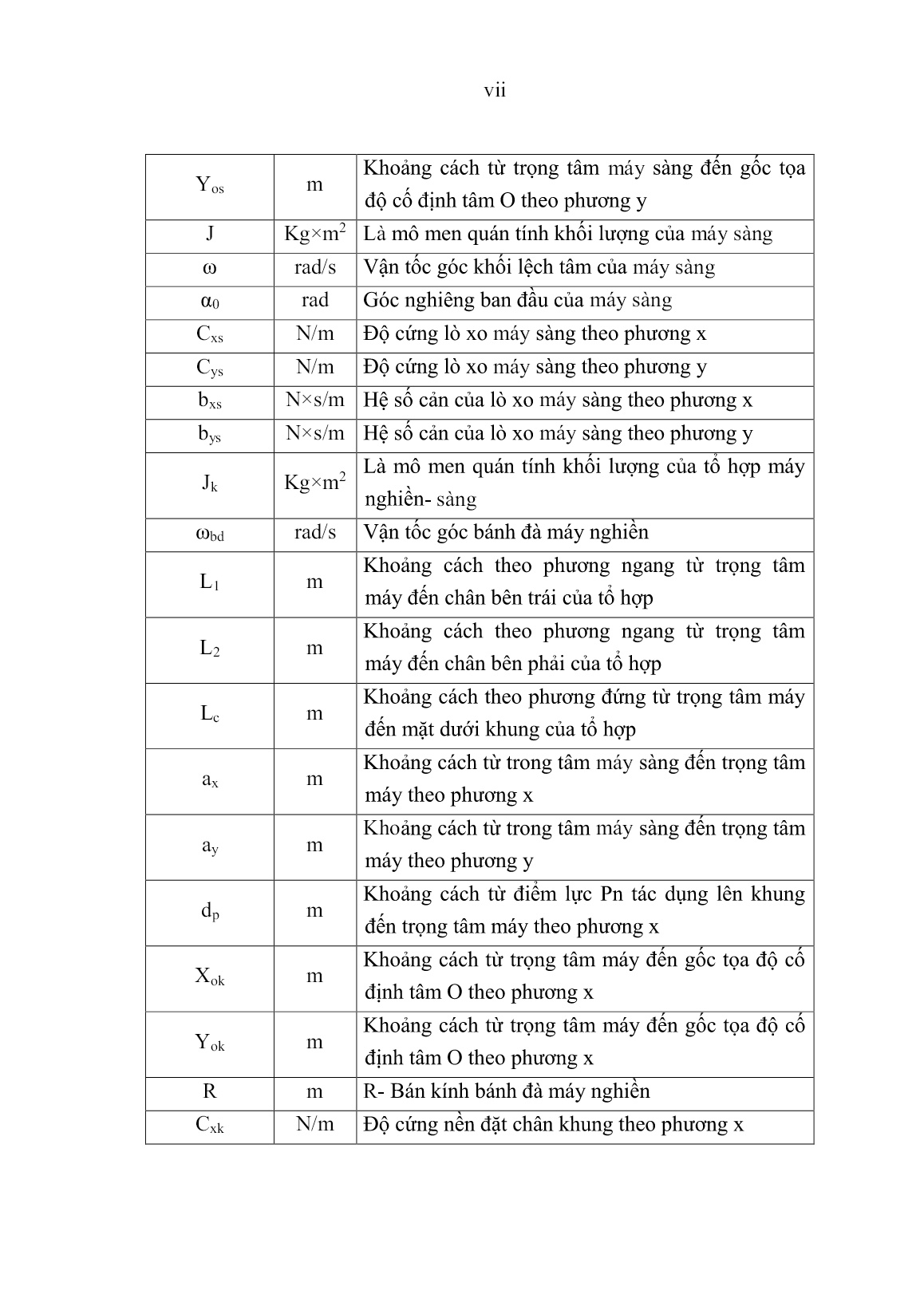
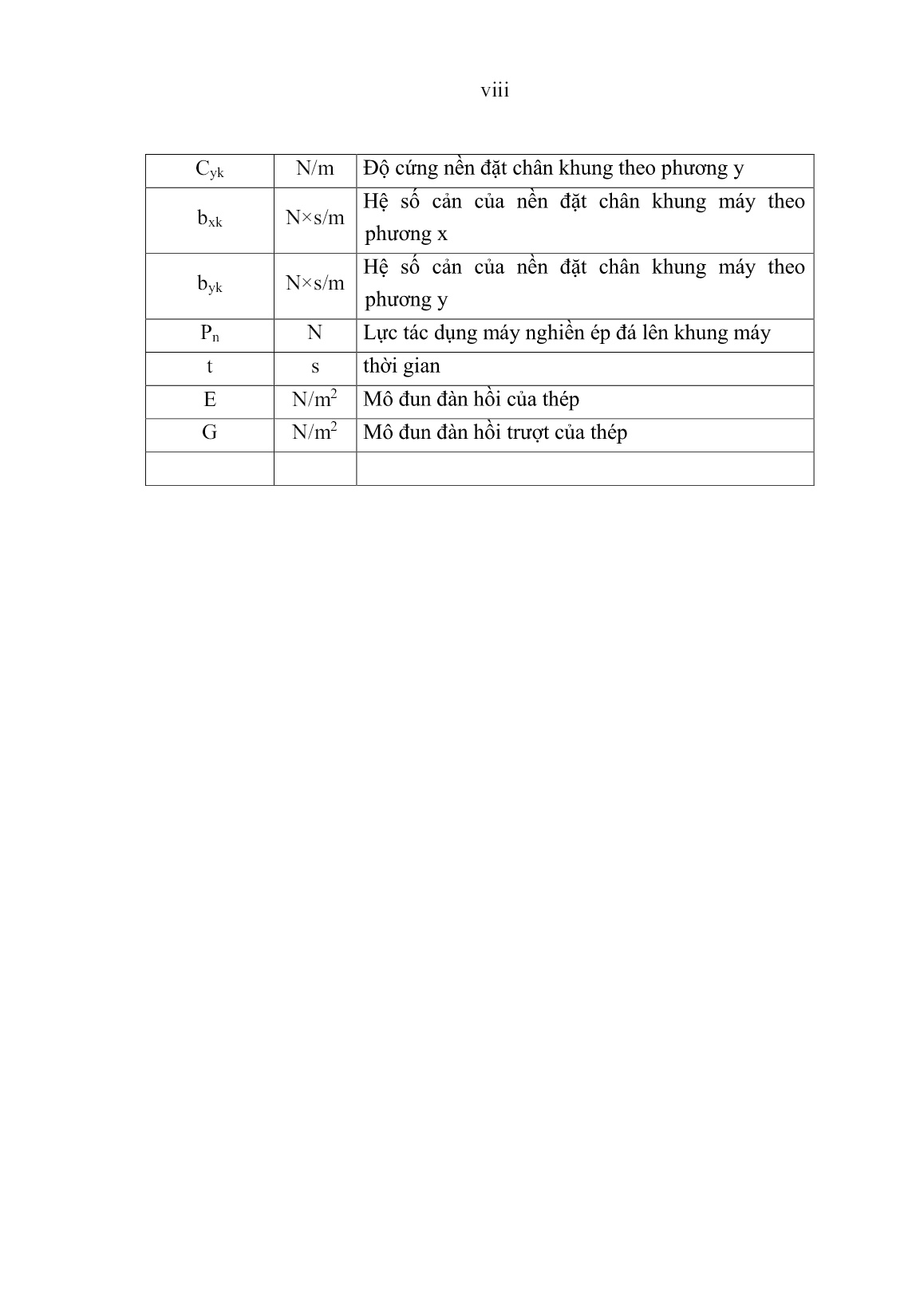
Luận án Nghiên cứu xác định một số thông số hợp lý của máy sàng rung vô hướng trên tổ hợp nghiền sàng di động

ng như của động cơ tác dụng lên khung theo 
công thức (2.20). 
- Lực nghiền đá (Fn) trên hàm nghiền tác dụng lên khung máy khi tổ hợp 
làm việc. 
R=2P.sin(β/2) (lực ép dọc theo phương y). P là lực làm vỡ viên đá (phụ 
thuộc vào độ bền của đá làm thí nghiệm và đo bằng thực nghiệm. 
Trong đó β là góc kẹp hàm nghiền β=18o. 
Do tính dối xứng của hàm nghiền nên giả thiết lực ép ngang (phương x), và 
lực dọc (phương y) tự cân bằng. Đặt Pn giá trị lực phương y với: Pn =R =2P. 
sin(β/2) nhưng ngược chiều, Pn là lực tác dụng lên khung theo phương y trong 
quá trình nghiền đá. Giả thiết quá trình ép đá chịu nén trong trạng thái biến dạng 
đang hồi. Khi đó lực ép đá tác dụng lên khung theo phương thẳng đứng (phương 
y) được xác định dưới dạng lực theo quỹ đạo chuyển động quay của bánh đà 
máy nghiền theo phương trình (2.21) dưới đây. 
n. bd bd
n . bd bd ]
P sin t sin t
F P.sin / 2 
[ ( ) ( )]
( ) [ ( ) ( ). sin t sin t
2
 
  
│ │
│ │ (2.21) 
- Tính lực rung động do máy nghiền và động cơ tác dụng lên khung tổ hợp 
nghiền sàng di động theo hai phương x và y. Do khối lượng lệch tâm của máy 
55 
nghiền và của động cơ không đổi. Giả thiết bỏ qua ảnh hưởng của lực khí nén 
động cơ, tốc độ quay trục động cơ và máy nghiền ổn định. Khi đó lực rung động 
do máy nghiền và động cơ tác dụng lên khung theo hai phương x, y sẽ có dạng 
f(x) = p(x).sin(ωt) và f(y) = p(y).cos(ωt). Trong đó p(x), p(y) là giá trị lực lớn 
nhất tác dụng theo hai phương x, y. 
- Cách xác định các lực p(x), p(y) bằng thực nghiệm như sau: 
Gọi Px, Py là giá trị trị lực lớn nhất tác dụng lên khung do khối lệch tâm của 
máy nghiền đá gây ra (đo bằng thực nghiệm). Khi đó lực tác dụng lên khung sẽ 
là Px .sin(ωbdt) và Py .cos(ωbdt). Thực tế các lực quay không cân bằng nhỏ hơn 
lực nghiền đá rất nhiều (Px, Py<< Pn ). 
Gọi Pdx, Pdy là giá trị trị lực lớn nhất tác dụng lên khung do lực quay không cân 
bằng của động cơ. Khi đó lực tác dụng lên khung sẽ là Pdx.sin(ωđct) và Pdy.cos(ωđct). 
Gọi Fđkx và Fdky là lực do máy nghiền và động cơ tác dụng lên khung tổ 
hợp nghiền sàng di động, khi đó lực rung động do máy nghiền và động cơ tác 
dụng lên khung tổ hợp nghiền sàng di động theo hai phương x và y được xác 
định theo công thức (2.22) sau: 
( ) ( )
( ) ( )
đkx x bd dx đc
đky y b dn d y đc
F t
F
P sin P sin t
P cos t P cosF t
 
 
 (2.22) 
Thay phương trình (2.21) vào ta được 
.
( ) ( )
( ) [ ( ) ( )]
( ) (
. / 2 .
)
đkx x bd dx đc
đky bd bd
y bd dy đc
F
n
P sin t P sin t
P sin si t sin t
P cos t P cos t
F
 
  
 
│ │ (2.23) 
Hệ phương trình (2.23) là các phương trình lực rung động do máy nghiền và 
động cơ tác dụng lên khung. 
* Thực nghiệm xác định giá trị lực trên tổ hợp TNS-05 
Để tính giá trị các lực lớn nhất ta đo đạc thực nghiệm dựa trên các ten-xơ 
biến dạng đặt tại chân máy sau đó tính theo công thức tính lực (2.24) 
56 
0
F
S
E l
l
 (2.24) 
Trong đó: E- Mô đun đàn hồi vật liệu chịu lực; S- Tiết diện đo; l0 - hiều dài 
ten-xơ đo; ∆l - biến dạng ten xơ. 
Quá trình thí nghiệm dùng các ten xơ biến dạng trên chân khung đỡ máy 
nghiền đá và chân khung của tổ hợp nên ta sẽ thu được biến dạng do máy nghiền 
đá gây ra và biến dạng do tổ hợp máy nghiền cùng động có gây ra, do đó ta sẽ 
tính hiệu biến dạng do tổ hợp máy nghiền cùng động cơ và do máy nghiền đá ta 
sẽ thu được biến dạng do động gây ra. 
Dưới đây là đồ thị đo giá trị biến dạng đo bằng thực nghiệm trên tổ hợp 
nghiền sàng di động TNS-05 ở chế độ làm việc đủ tải và tốc độ trục lệc tâm sàng 
ωs=120 (rad/s) cho ta giá trị đồ thị biến dạng sau: 
- Đồ thị giá trị đo biến dạng do máy nghiền tạo ra 
Hình 2-5. Biến dạng do tác động của máy nghiền theo phương ngang (phương x) 
Hình 2-6. Biến dạng do tác động của máy nghiền theo phương đứng (phương y) 
- Đồ thị đo biến dạng do máy nghiền và động cơ tạo ra. 
Hình 2-7. Biến dạng do tác động của máy nghiền và động cơ theo phương 
ngang (phương x) 
57 
Hình 2-8. Biến dạng do tác động của máy nghiền và động cơ theo phương đứng 
(phương y) 
∆lxn , ∆lyn - là biến dạng do lực rung của máy nghiền sinh ra theo phương x,y. 
∆lynd , ∆lxnd - là biến dạng do lực rung của máy nghiền cùng với động cơ 
sinh ra theo phương x, y. 
Tiến hành tính biến dạng do lực rung của máy nghiền sinh ra theo phương x, 
từ đồ thị ta chọn các giá trị ∆lxn1, ∆lxn2, , ∆lxnn với n= 1, 2,, n là số tự nhiên. 
Tính được ∆lxn theo công thức (2.25) sau 
 1 2
...xn x xnn
xn
n
l l l
l
 (2.25) 
Tương tự ta cũng tính được biến dạng do lực rung của máy nghiền theo 
phương y và biến dạng do lực rung của máy nghiền cùng với động cơ sinh ra 
theo phương x,y. 
Thay các giá trị biến dạng đo được thể hiện trên các đồ thị từ hình 2-6 đến 
hình 2-7 vào (2.25) sẽ được giá trị biến dạng thực tế bằng thực nghiệm. 
Thay các giá trị biến dạng đo được vào công thức (2.20) tính được lực rung 
lớn nhất do máy nghiền gây ra theo phương y là 
Ta có : Fyn= Pn+Py = ky.│ ∆lyn │ 
Với: ky=E.
0
S
l
 Trong thực nghiệm S là tiết diện chân gắn ten xơ 
 Thay số ta được: ky=217143.105.
5
3
1,7.10
5.10
= 7168420 (N/m) 
Từ đó tính được: Fyn= 7168420.│ -0.39.10-3 │=2800 (N) 
- Thực nghiệm đo lực ép đá lớn nhất P=7750 (N) Pn=2480 (N). 
Từ đó tính được: Py= 2800-2480=320(N). 
- Tương tự tính lực rung lớn nhất do máy nghiền theo phương x gây ra 
58 
Fxn= kx.│ ∆lxn │. Với Fxn= Px. 
kx = E.
0
S
l
 = 217143.105.
5
3
1,2.10
5.10
=5067147 (N/m) 
Thay số Px=5067147. │ -0.086.10-3 │= 435.76 (N) 
- Tính lực rung lớn nhất do động cơ gây ra theo phương y 
Pyd= Fyd = Pynd- Fyn. 
Pynd= ky.│ ∆lyn │=7168420.│ -0.495.10-3 │= 3548,4 (N). 
Pyd =3548,4 -2800 = 748,4 (N) 
- Tính lực rung lớn nhất do động cơ gây ra theo phương x 
Pxd= Fxd = Pxnd- Pdn. 
Pxnd= 5067147. │ -0.138.10-3 │=699,3 (N). 
Pxd= Fxd = Pxnd- Pdn =699,3-435.76 =263.54(N) 
Thay các giá trị lực tính bằng thực nghiệm ở trên vào (2.23) được hệ lực tác 
dụng lên khung tổ hợp nghiền sàng di động theo hai phương x và y mô phỏng 
dưới dạng lực F(x) và F(y) theo quỹ đạo quay của trục bánh đà và trục động cơ 
dẫn động theo (2.26) dưới đây: 
.
( ) 435.76 ( ) 263.54 ( )
( ) 7750 ( ) [ ( ) ( )]
320 (
/
) 748.4
.
)
2 .
(
đkx bd đc
đky bd bd
bd đc
F sin t sin t
sin sin t sin t
co t
x F
F
s c
F
o
y
s t
 
  
 
│ │ (2.26) 
Đây là các phương trình lực rung động do máy nghiền và động cơ tác dụng 
lên khung và được thêm vào hệ PTVP khi giải bài toán ĐLH của máy sàng rung 
vô hướng trên tổ hợp nghiền sàng di động TNS-05. 
2.2. Phương pháp thiết lập phương trình vi phân chuyển động 
Để khảo sát được động lực học máy sàng rung trên tổ hợp nghiền sàng di 
động, vấn đề quan trọng nhất là phải thiết lập được phương trình chuyển động. 
 Từ mô hình động lực học của tổ hợp (hình 2-2) có số bậc tự do là 6, tương 
ứng với 6 toạ độ suy rộng, viết phương trình chuyển động đối với các toạ độ này. 
59 
Ta sử dụng phương pháp Đalambe để thiết lập phương trình vi phân 
chuyển động của máy sàng rung trên tổ hợp nghiền sàng di động. Với tổ hợp 
nghiền sàng di động (mô hình phẳng), tiến hành tách các liên kết đàn hồi tại 2 lò 
xo liên kết giữa máy sàng với khung máy thay bởi các liên kết lực theo phương 
x,y. Tương tự tại 2 chân máy đứng trên nền đàn hồi ta cũng tách liên kết và thay 
bởi các các lực liên kết theo hai phương x,y. 
Sau khi đưa thêm các thành phần lực quán tính theo phương X,Y và mô 
men quán tính theo trục Z vào tổ hợp các lực tác dụng lên tổ hợp nghiền sàng di 
động, mô hình khảo sát động lực học của máy sàng rung vô hướng trên tổ hợp 
nghiền sàng di động sẽ được thể hiện như hình 2-9. 
Để thiết lập hệ phương trình vi phân chuyển động của máy sàng rung trên 
tổ hợp nghiền sàng di động có tính đến ảnh hưởng rung động của cụm máy 
nghiền, động cơ và tính đàn hồi của nền đất thì trước tiên sẽ thiết lập hệ phương 
trình vi phân chuyển động của phần máy sàng và sau đó là phần khung tổ hợp, 
tổng hợp lại sẽ được hệ phương trình vi phân chuyển động của máy sàng rung 
trên tổ hợp nghiền sàng di động. 
Hình 2-9. Sơ đồ liên kết lực trên máy sàng và khung tổ hợp 
60 
 * Viết hệ phương trình vi phân với máy sàng 
Hệ lực tác dụng lên máy sàng được thể hiện trên hình 2-10. 
Hình 2-10. Sơ đồ các lực tác dụng và chuyển vị máy sàng 
Trong đó đặt: 
1 1 1 1 1
2 2 2 2 2
1 1 1 1 1
2 2 2 2 2
x x x
x x x
y y y
y y y
F b x C x
F b x C x
F b y C y
F b y C y
Từ đó, ta thiết lập được các phương trình cân bằng tĩnh động theo phương 
X, phương Y và trục Z. Hệ phương trình vi phân chuyển động của máy sàng là: 
.sin( )
cos( )
[ cos ) sin )]
[ cos ) sin )] [ cos )
sin ) [ co
2
x1 1 x1 1 x2 2 x2 2 0 0
2
y1 1 y1 1 y2 2 y2 2 0 0
y1 1 1 0 2 0
y1 1 1 0 2 0 y2 2 2 0
2 0 y2 2 2
mX b x C x b x C x m r t
mY b y C y b y C y m r t
J b y l b
C y l b b y l
b C y l
   
   
 
  
  
  s ) sin )]
[ sin ) cos )] [ sin )
cos )] [ sin ) cos )]
[ sin ) cos )] sin( )
0 2 0
x1 1 1 0 2 0 x1 1 1 0
2 0 x2 2 2 0 2 0
2
x2 2 2 0 2 0 0 0
b
b x l b C x l
b b x l b
+ C x l b em r t
  
   
   
  
   
 (2.27) 
Với: 
os s os sX X x ; Y Y y 
61 
Biểu diễn các thông số x1, x2, y1, y2 và các đạo hàm của chúng theo các biến 
X, Y và  . 
Hình 2-11. Sơ đồ xác định lực và cánh tay đòn của lực trên máy sàng. 
Dựa vào hình 2-10 và hình 2-11, ta có quan hệ giữa các tham số theo hai 
phương X, Y như sau: 
- Theo phương X: 
+ Vị trí ban đầu: 01 1 0 2 0cos sinx l b 
 02 2 0 2 0
cos sinx l b 
 + Vị trí đang xét:
11 1 0 2 0cos ) sin ) sx l b x  
22 2 0 2 0
cos( ) sin( )x l b   
11 11 0 0 2 0 001 [cos cos )] [sin sin )] sl bx xx x   
1 0 0 0
2 0 0 0
1 [cos (cos .cos sin .sin )]
[sin (sin .cos cos .sin )] s
l
b
x
x
 
 
Do góc θ rất nhỏ nên cosθ≈1. sinθ≈θ nên có: 
1 0 0 0 2 0 0 0
1 0 2 0
1
1
[cos cos .sin )] [sin .cos sin )]
: . .sin . .cos
s
s
x
x
l b x
Hay l b x
  
  
-
2 22 2 0 0 2 0 0
2 2 0 0 0 2 0 0 0
2 2 0 2 0
02 [cos cos )] [sin sin )]
[cos (cos .sin )] [sin ( .cos sin )]
. .sin . .cos
s
s
s
l b xx x x
x l b x
Ha l xxy b
  
   
  
 - Theo phương Y: 
 + Vị trí ban đầu: 
62 
01 1 0 2 0
02 2 0 2 0
sin cos
cos sin
y l b
y b l
+ Vị trí đang xét: 
11 1 0 2 0
12 2 0 2 0
sin ) cos )
cos ) sin )
s
s
y l b y
y b l y
  
  
1 11 01 1 0 0 2 0 0
2 12 02 2 0 0 2 0 0
1 1 0 0 0 2 0 0 0
2 2 0 0 0
[sin sin )] [cos cos )]
[cos cos )] [sin sin )]
[sin ( .cos sin )] [cos (cos .sin )]
[cos (cos .sin )]
s
s
s
s
y y y y l b
y y y y b l
y y l b
y y b
   
   
   
  
 2 0 0 0
1 1 0 2 0
2 2 0 2 0
[sin ( .cos sin )]
. .cos . .sin
. .sin . .cos
s
s
l
y y l b
y y b l
  
  
  
 Thay các giá trị trên vào (2.27) ta được: 
( . .sin . .cos ) ' ( . .sin . .cos )
( . .sin . .cos ) ' ( . .sin . .cos ) .sin( )
( . .cos . .sin ) ' ( . .cos .
x1 1 0 2 0 s x1 1 0 2 0 s
2
x2 2 0 2 0 s x2 2 0 2 0 s 0 0
y1 s 1 0 2 0 y1 s 1 0 2
mX b l b x C l b x
b l b x C l b x m r t
mY b y l b C y l b
    
    
   
  
 .sin )
( . .sin . .cos ) ' ( . .sin . .cos ) cos( )
( . .cos . .sin ) '.[ (cos .sin ) ( .cos sin )]
[ (cos .sin ) ( .cos sin )]
0
2
y2 s 2 0 2 0 y2 s 2 0 2 0 0 0
y1 s 1 0 2 0 1 0 0 2 0 0
y1 1 1 0 0 2 0 0
b y b l C y b l m r t
J b y l b l b
C y l b
 
    
     
   
  
 ( . .sin . .cos ) '.[ (cos .sin ) ( .cos sin )
[ (cos .sin ) ( .cos sin )
( . .sin . .cos ) '.[ ( .cos sin ) (cos .sin )]
[ ( .cos sin
y2 2 0 2 0 2 0 0 2 0 0
y2 2 2 0 0 2 0 0
x1 1 0 2 0 s 1 0 0 2 0 0
x1 1 1 0
b y b l l b
C y l b
b l b x l b
C x l
    
   
   
 
 
 
 ) (cos .sin )]
( . .sin . .cos ) '[ ( .cos sin ) (cos .sin )]
[ ( .cos sin ) (cos .sin )] sin( )
0 2 0 0
x2 2 0 2 0 s 2 0 0 2 0 0
2
x2 2 2 0 0 2 0 0 0 0
b
b l b x l b
+ C x l b em r t
 
   
 
   
 (2.28) 
 Do: 
x1 x2 xs y1 y2 ys
x1 x2 xs y1 y2 ys
C C C ; C C C ;
b b b ; b b b ;
Khai triển các đạo hàm ta được: 
63 
1 1 0 2 0 1 1 0 2 0
2
2 2 0 2 0 2 2 0 2 0 0 0
1 1 0 2 0 1 1 0 2
( . .sin . .cos ) ' ( . .sin . .cos )
( . .sin . .cos ) ' ( . .sin . .cos ) .sin( )
( . .cos . .sin ) ' ( . .cos .
x s x s
x s x s
y s y s
mX b l b x C l b x
b l b x C l b x m r t
mY b y l b C y l b
    
    
   
  
 0
2
2 2 0 2 0 2 2 0 2 0 0 0
1 1 0 2 0 1 0 0 2 0 0
1 1 1 0 0 2 0 0
.sin )
( . .sin . .cos ) ' ( . .sin . .cos ) cos( )
( . .cos . .sin ) '.[ (cos .sin ) ( .cos sin )]
[ (cos .sin ) ( .cos sin )]
y s y s
y s
y
b y b l C y b l m r t
J b y l b l b
C y l b
 
    
     
   
  
 2 2 0 2 0 2 0 0 2 0 0
2 2 2 0 0 2 0 0
1 1 0 2 0 1 0 0 2 0 0
1 1 1 0
( . .sin . .cos ) '.[ (cos .sin ) ( .cos sin )
C [ (cos .sin ) ( .cos sin )
b ( . .sin . .cos ) '.[ ( .cos sin ) (cos .sin )]
C [ ( .cos sin
y
y
x s
x
b y b l l b
y l b
l b x l b
x l
    
   
   
 
 
 
 0 2 0 0
2 2 0 2 0 2 0 0 2 0 0
2
2 2 2 0 0 2 0 0 0 0
) (cos .sin )]
b ( . .sin . .cos ) '[ ( .cos sin ) (cos .sin )]
+ C [ ( .cos sin ) (cos .sin )] sin( )
x s
x
b
l b x l b
x l b em r t
 
   
 
   
1 1 0 2 0 1 1 0 2 0
2
2 2 0 2 0 2 2 0 2 0 0 0
1 1 0 2 0 1 1 0 2
[( .sin .cos ) ] [( .sin .cos ) ]
[( .sin .cos ) ] [( .sin .cos ) ] .sin( )
[ ( .cos .sin ) ] [ ( .cos .si
x s x s
x s x s
y s y s
mX b l b x C l b x
b l b x C l b x m r t
mY b y l b C y l b
  
  
  
  
0
2
2 2 0 2 0 2 2 0 2 0 0 0
1 1 0 2 0 1 0 2 0 1 0 2 0
1 1 0 2 0 1 0
n ) ]
[ ( .sin .cos ) ] [ ( .sin .cos ) ] cos( )
[( .sin .cos ) ].[( .cos .sin ) ( .sin .cos ) ]
.[ ( .cos .sin ) ].[( .cos
y s y s
y s
y s
b y b l C y b l m r t
J b l b x l b l b
C y l b l
 
  
  
  
  
 2 0 1 0 2 0
2 2 0 2 0 2 0 2 0 2 0 2 0
2 2 0 2 0 2 0 2 0 2 0 2 0
1 1 0 2
.sin ) ( .sin .cos ) ]
[ ( .sin .cos ) ].[( .sin .cos ) ( .sin .cos )
C .[ ( .sin .cos ) ].[( .sin .cos ) ( .sin .cos )
b [( .sin .co
y s
y s
x
b l b
b y b l b l l b
y b l b l l b
l b
 
  
  
 
 
 0 1 0 2 0 1 0 2 0
1 1 0 2 0 1 0 2 0 1 0 2 0
2 2 0 2 0 2 0 2 0 2 0 2 0
s ) ].[( .sin .cos ) ( .cos .sin ) ]
C [( .sin .cos ) ].[( .sin .cos ) ( .cos .sin ) ]
b [( .sin .cos ) ].[( .sin .cos ) ( .sin .cos )
s
x s
x s
x l b l b
l b x l b l b
l b x l b b l
  
  
  
2 2 0 2 0 2 0 2 0
2
2 0 2 0 0 0
]
+ C [( .sin .cos )( ].[( .sin .cos )
( .sin .cos ) ] sin( )
x sl b x l b
b l em r t

  
 
  
64 
1 1 0 2 0 1 1 0 2 0
2
2 2 0 2 0 2 2 0 2 0 0 0
1 1 0 2 0 1 1 0 2
[( .sin .cos ) ] [( .sin .cos ) ]
[( .sin .cos ) ] [( .sin .cos ) ] .sin( )
[ ( .cos .sin ) ] [ ( .cos .si
x s x s
x s x s
y s y s
mX b l b x C l b x
b l b x C l b x m r t
mY b y l b C y l b
  
  
  
  
0
2
2 2 0 2 0 2 2 0 2 0 0 0
1 1 0 2 0 1 0 2 0 1 0 2 0
1 1 0 2 0 1 0 2
n ) ]
[ ( .sin .cos ) ] [ ( .sin .cos ) ] cos( )
[ ( cos sin ) ].[( .cos .sin ) ( .sin .cos ) ]
.[ ( .cos .sin ) ].[( .cos
y s y s
y s
y s
b y b l C y b l m r t
J b y l b l b l b
C y l b l b
 
  
  
  
  
 0 1 0 2 0
2 2 0 2 0 2 0 2 0 2 0 2 0
2 2 0 2 0 2 0 2 0 2 0 2 0
1 1 0 2
.sin ) ( .sin .cos ) ]
[ ( .sin .cos ) ].[( .sin .cos ) ( .sin .cos )
C .[ ( .sin .cos ) ].[( .sin .cos ) ( .sin .cos )
b [( .sin .cos
y s
y s
x
l b
b y b l b l l b
y b l b l l b
l b
 
  
  
 
 
 0 1 0 2 0 1 0 2 0
1 1 0 2 0 1 0 2 0 1 0 2 0
2 2 0 2 0 2 0 2 0 2 0 2 0
) ].[( .sin .cos ) ( .cos .sin ) ]
C [( .sin .cos ) ].[( .sin .cos ) ( .cos .sin ) ]
b [( .sin .cos ) ].[( .sin .cos ) ( .sin .cos ) ]
s
x s
x s
x l b l b
l b x l b l b
l b x l b b l
 
  
  
2 2 0 2 0 2 0 2 0 2 0
2
2 0 0 0
+ C [( .sin .cos )( ].[( .sin .cos ) ( .sin
.cos ) ] sin( )
x sl b x l b b
l em r t
  
 
  
Đặt: 
.sin .cos ;
q .sin .cos ;
q .cos .sin ;
q .cos .sin ;
q l b
l b
l b
l b
1 1 0 2 0
2 2 0 2 0
3 1 0 2 0
4 2 0 2 0
Ta có: 
1 2 1 2
1 2 1 2
; ;
; ;
x x xs y y ys
x x xs y y ys
C C C C C C
b b b b b b
Thay vào hệ phương trình trên ta được: 
( . ) ( . ) ( . ) ( . ) .sin( )
( . ) ( . ) ( ) ( ) cos( )
(y . ).( ) .( ).( )
2
xs 1 s xs 1 s xs 2 s xs 2 s 0 0
2
ys s 3 ys s 3 ys s 4 ys s 4 0 0
ys s 3 3 1 ys s 3 3 1
mX b q x C q x b q x C q x m r t
mY b y q C y q b y q C y q m r t
J b q q q C y q q q b
   
   
    
  
  
 ( ).( )
.( ).( ) ( ).( ) ( ).( )
( ).( ) ( ).( ) sin( )
ys s 4 4 2
ys s 4 4 2 xs 1 s 1 3 xs 1 s 1 3
2
xs 2 s 2 4 xs 2 s 2 4 0 0
y q q q
C y q q q b q x q q C q x q q
b q x q q + C q x q q em r t
 
     
   
   
65 
. . ( ). ( ). .sin( )
. . ( ). ( ). cos( )
. y . .
2
xs s xs s xs 1 2 xs 1 2 0 0
2
ys s ys s ys 3 4 ys 3 4 0 0
2 2
ys 1 s ys 1 3 ys 3 s ys 3 ys s 3 ys s 1 ys 3
mX 2C x 2b x C q q b q q m r t
mY 2C y 2b y C q q b q q m r t
J b q b q q b q y b q C y q C y q C q
 
 
      
  
  
.
2
ys 3 1
2 2 2
ys s 4 ys 2 s ys 4 ys 4 2 ys s 4 ys s 2 ys 4 ys 4 2
2 2 2
xs 1 xs 1 3 xs 1 s xs 3 s xs 1 xs 1 3 xs 1 s xs 3 s
2
xs 2 xs 2 4 xs 2 s xs 4 s
C q q
b y q b q y b q b q q C y q C y q C q C q q
b q b q q b q x b q x C q C q q C q x C q x
b q b q q b q x -b q x + C

      
     
   
 sin( )2 2 2xs 2 xs 2 4 xs 2 s xs 4 s 0 0q C q q + C q x - C q x em r t  
   
. . ( ). ( ). .sin( )
. . ( ). ( ). cos( )
( ) ( ) ( )
( )
2
xs s xs s xs 1 2 xs 1 2 0 0
2
ys s ys s ys 3 4 ys 3 4 0 0
2 2 2 2 2
ys 3 1 4 2 xs 3 1 4 2 xs 1 2 3 4
ys 1 2 s
mX 2C x 2b x C q q b q q m r t
mY 2C y 2b y C q q b q q m r t
J [C q q q q C q q q q ] {C q q q q
C q q y
 
 
 
  
  
 ( ) ( ) ( )
( ) ( ) . )
( ) ( ) ( ) ( ) sin( )
xs 3 4 s ys 1 2 s xs 3 4 s
2 2 2 2
ys 1 3 2 4 xs 1 3 2 4 xs 1 xs 2 ys 3 ys 4
2
xs 1 2 s xs 1 2 s ys 3 4 s ys 3 4 s 0 0
C q q x b q q y b q q x
[b q q q q b q q q q ] } b q b q b q b q
C q + q x b q q x C q q y b q q y em r t
  
   
 (2.29) 
 * Viết hệ phương trình vi phân với phần khung 
Đặt 
xk 3 x3 3 x3 3
xk 4 x4 4 x4 4
yk 3 y3 3 y3 3
yk 4 y4 4 y4 4
F b x C x
F b x C x
F b y C y
F b y C y
Hệ lực tác dụng lên khung máy được thể hiện trên hình 2-12 
Hình 2-12. Sơ đồ các lực tác dụng và chuyển vị của khung máy 
66 
Từ hệ lực tác dụng lên khung có hệ phương trình vi phân chuyển động của 
máy khung là: 
sin( t) sin( t)
cos( t) cos( t)
(d cos s
ck x1 1 x1 1 x2 2 x2 2 x3 3 x3 3 x4 4 x4 4
x bd dx dc
ck y1 1 y1 1 y2 2 y2 2 y3 3 y3 3 y4 4 y4 4
y bd dy dc n
k k y1 1 1 k c
MX b x C x b x C x b x C x b x C x
P P 0
MY b y C y b y C y b y C y b y C y
P P F 0
J b y L
 
 
 
 in ) (d cos sin )
(d cos sin ) (d cos sin )
(L cos sin ) (L cos sin )
(L cos sin ) (L cos sin )
(d sin cos )]
k y1 1 1 k c k
y2 2 2 k c k y2 2 2 k c k
y3 3 1 k c k y3 3 1 k c k
y4 4 2 k c k y4 4 2 k c k
x1 1 1 k c k x1
C y L
b y L C y L
b y L C y L
b y L C y L
-b x L C
  
   
   
   
 
 (d sin cos )
(d sin cos )] (d sin cos )
(L sin cos )] (L sin cos )
(L sin cos ) (L sin cos )
1 1 k c k
x2 2 2 k c k x2 2 2 k c k
x3 3 1 k c k x3 3 1 k c k
x4 4 2 k c k x4 4 2 k c k n p
x L
-b x L C x L
b x L C x L
b x L + C x L F d 0
 
   
   
   
 (2.30) 
Với : 
ck ok k ck 0k k
X X x , Y Y y , 
Tương tự phần tính máy sàng, ta tính lực tác dụng lên khung máy 
Dựa vào hình 2-12 và hình 2-13 có: 
- Theo phương x: 
Vị trí ban đầu:
03 1x L , 
Hình 2-13. Sơ đồ xác định lực và cánh tay đòn của lực trên khung máy 
67 
+ Vị trí đang xét: 
33 1 .cos .sink c k kx L L x  
 cos sin3 33 03 1 k c k kx x x L . 1 L . x ;  
Do góc θ rất nhỏ nên 
k k kcos 1; sin   nên có: 
3 c k kx L . x ; 
Tương tự có : . cos .sin . ;4 44 04 2 k c k k c k kx x x L 1 L x L x   
- Theo phương y: 
+ Vị trí ban đầu: 
03 04 cy y L , 
+ Vị trí đang xét: 
sin cos33 1 k c k k 1 k c ky L . L . y L . L y ;   
 sin cos44 2 k c k k 2 k c kY L . L . y L . L y ;   
3 33 03 1 k ky y y L . y ; 
4 44