Luận án Nghiên cứu xây dựng mô hình quá trình truyền nhiệt bên trong vật nung

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
Trang 6

Trang 7

Trang 8
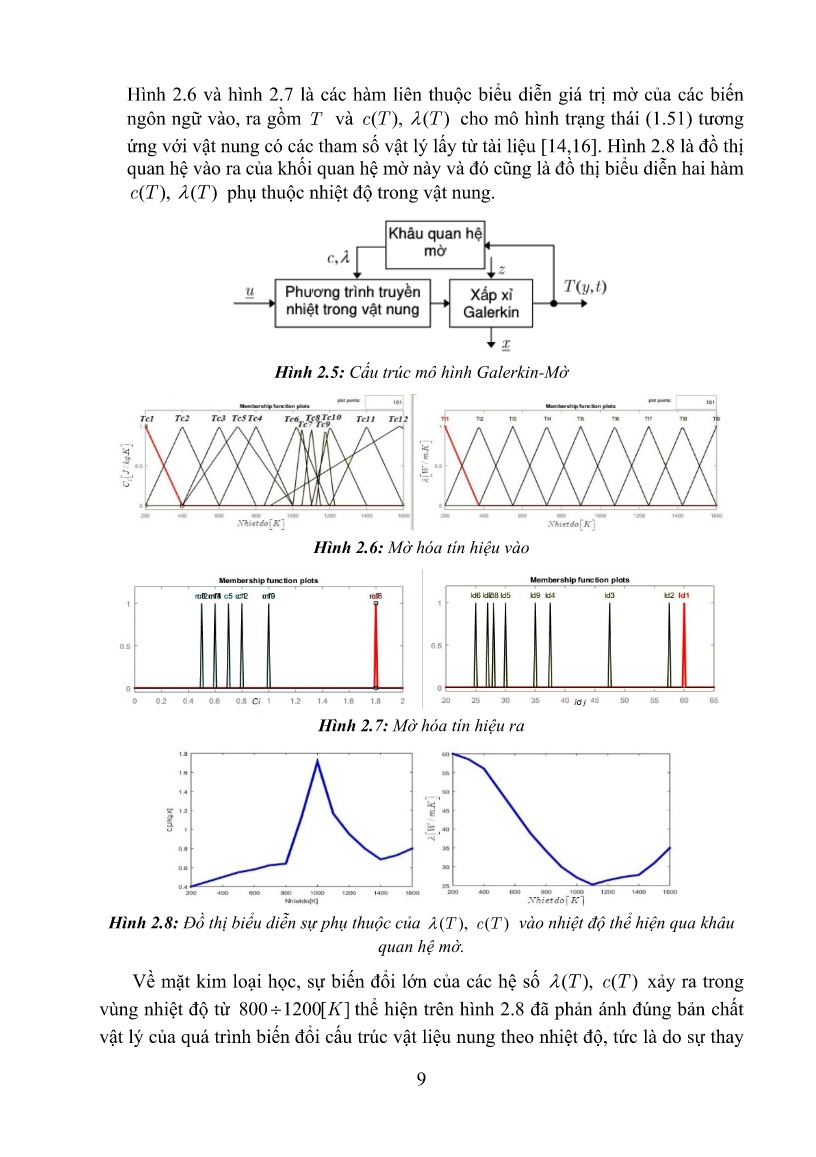
Trang 9
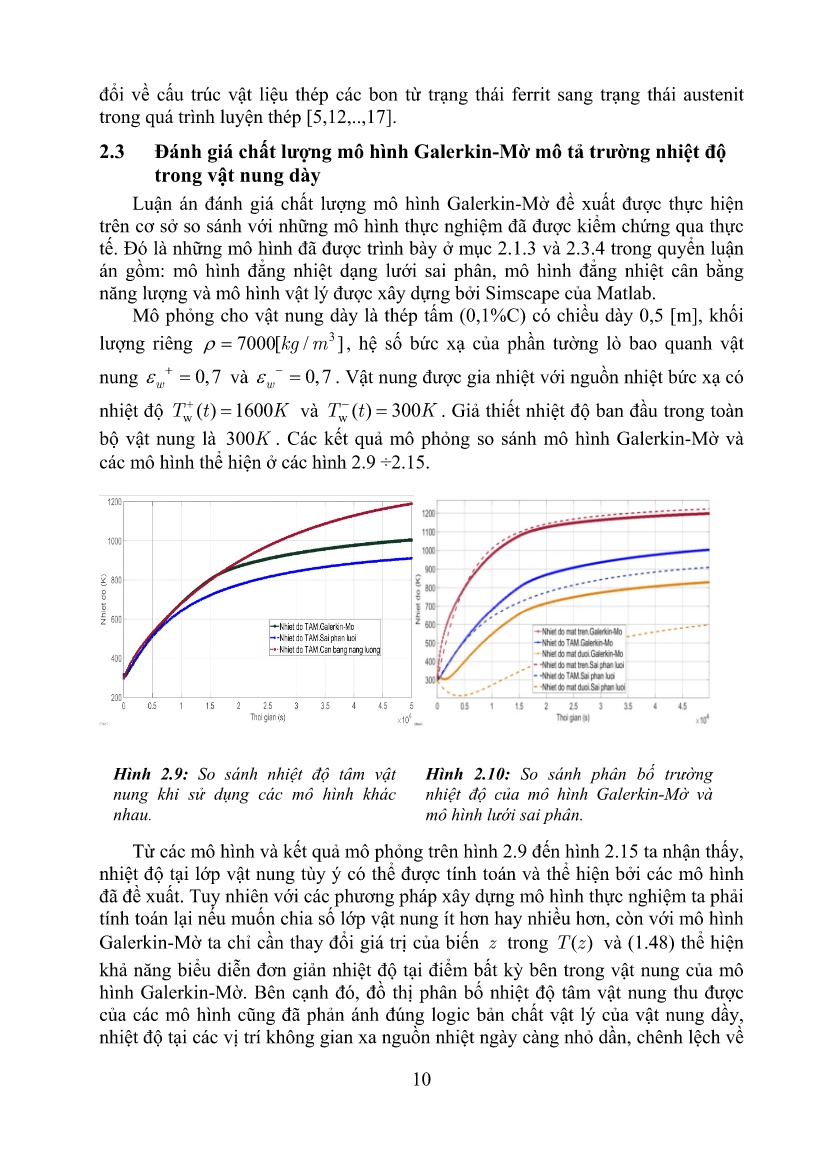
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Luận án Nghiên cứu xây dựng mô hình quá trình truyền nhiệt bên trong vật nung", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Luận án Nghiên cứu xây dựng mô hình quá trình truyền nhiệt bên trong vật nung

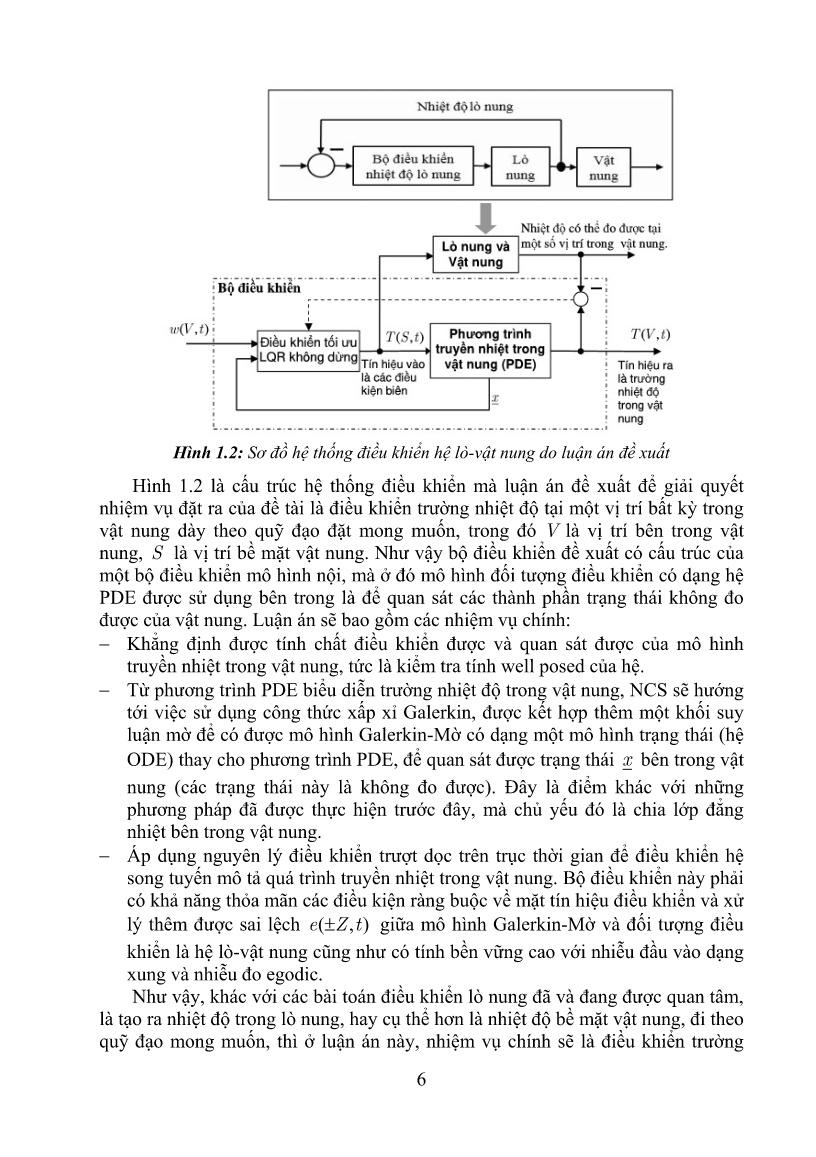
cũng như có tính bền vững cao với nhiễu đầu vào dạng xung và nhiễu đo egodic. Như vậy, khác với các bài toán điều khiển lò nung đã và đang được quan tâm, là tạo ra nhiệt độ trong lò nung, hay cụ thể hơn là nhiệt độ bề mặt vật nung, đi theo quỹ đạo mong muốn, thì ở luận án này, nhiệm vụ chính sẽ là điều khiển trường 6 nhiệt độ tại một vị trí V bất kỳ của vật nung dày trong lò nung. Rõ ràng, khi kết hợp thêm với bộ điều khiển nhiệt độ lò nung phía bên ngoài vật nung (hình 1.2), ta sẽ được một hệ thống điều khiển vòng kín điều khiển sự phân bố trường nhiệt độ của bản thân vật nung nằm trong lò. Hệ thống đó sẽ giúp phần nâng cao được chất lượng sản phẩm của quá trình nung. Do đó luận án có ý nghĩa thiết thực trong thực tế. CHƯƠNG 2: XÂY DỰNG MÔ HÌNH QUÁ TRÌNH TRUYỀN NHIỆT BÊN TRONG VẬT NUNG Luận án xuất phát từ các nghiên cứu về mô hình truyền nhiệt trong vật nung bằng các phương pháp lý thuyết và thực nghiệm. Qua đó, tác giả đề xuất xây dựng mô hình truyền nhiệt trong vật nung từ phương trình PDE kết hợp với phương pháp tách biến Galerkin và quan hệ mờ để mờ hóa hai tham số c( T ), ( T ) của vật liệu phụ thuộc theo nhiệt độ. Kết quả thu được một mô hình trạng thái song tuyến phù hợp với mục đích điều khiển trường nhiệt độ trong vật nung dày. Tiếp theo, luận án sẽ tiến hành mô phỏng và so sánh mô hình đề xuất với một số mô hình thực nghiệm đã công bố. 2.1 Tổng quan về mô hình truyền nhiệt trong vật nung Từ các nghiên cứu về các phương pháp lý thuyết mô tả phương trình truyền nhiệt trong vật nung và các phương pháp số để tìm nghiệm gần đúng cho mô hình lý thuyết PDE và các nghiên cứu về mô hình thực nghiệm chia lớp đẳng nhiệt vật nung, luận án đi đến nhận xét: Để có mô hình phù hợp mục tiêu điều khiển, thì cần phải giải phương trình PDE. Tuy nhiên việc sử dụng các phương pháp số để giải gần đúng và mô hình thực nghiệm chưa đưa ra được mô hình trạng thái đủ đơn giản để mô tả trường nhiệt độ bên trong vật nung, nhất là chưa đủ thích hợp để có thể xây dựng được bộ điều khiển tối ưu thỏa mãn các điều kiện ràng buộc đặt ra. 2.2 Xây dựng mô hình truyền nhiệt bên trong vật nung Mục tiêu xây dựng mô hình truyền nhiệt bên trong vật nung tĩnh với chiều dày z Z 2 của luận án là: Kết hợp suy luận mờ và công thức tách biến Galerkin để mô hình hóa quá trình truyền nhiệt trong vật nung dày được mô tả bởi phương trình PDE: dT( z , t ) 1 T ( z , t ) ()z (1.47) dt c() z z z 3 trong đó [kg m ] là khối lượng riêng của vật nung, c [ J kgK ] nhiệt dung riêng của vật nung, [W mK ] là hệ số dẫn nhiệt của vật nung. Sử dụng phương pháp tách biến Galerkin chuyển nghiệm T(,) z t thành tổng tuyến tính của các các hàm một biến trên hệ trục tọa độ h1( z ), h 2 ( z ), h 3 ( z ) trong không gian ba chiều [14,16]: 7 2 3 2z 2 z 1 T(,)()() z t hi z x i t với h1() z 1, h 2 () z , h 3 () z (1.48) i 1 ZZ 3 có các hàm ảo gồm x1( t ), x 2 ( t ), x 3 ( t ) độc lập tuyến tính, giữ vai trò như biến trạng thái. Các hàm hi ( z ), i 1,2,3 được xem như hệ trục tọa độ biến thiên theo vị trí z trong vật nung. Tuy nhiên, khi sử dụng công thức xấp xỉ Galerkin (1.48) cho mô hình (1.47) thì ở tài liệu [14-20], mô hình ODE thu được lại xuất hiện các biến tham số trung bình i, c i , i 1,2,3 của vật nung, phụ thuộc hi ( z ), i 1,2,3 , thay cho c( T ), ( T ) ban đầu. Chính vì vậy, sau đây NCS sẽ đề xuất phương án sử dụng kỹ thuật mờ để xác định c( T ), ( T ) phụ thuộc vào nhiệt độ, vì T(,) z t là hàm của z , thay vì phải xác định i, c i , i 1,2,3 giúp cho nó dễ ứng dụng vào điều khiển hơn và hợp lý theo quan điểm về mặt vật liệu học [5,14,..,59]. Phương án đề xuất mờ hóa đã được NCS tiến hành mô phỏng và đánh giá ở công trình khoa học số [1]. Mô hình Galerkin có thêm khâu quan hệ mờ như mô tả ở hình 2.5, được luận án gọi là mô hình Galerkin-mờ, gồm hai thành phần: 1. Thành phần thứ nhất là một mô hình trạng thái cho bởi [14,15,16]: 0 0 0 1 1 12 (T ) 1 x 0 1 0 x 3 3 u 2 c() T Z c() T Z (1.51) 0 0 5 7.5 7.5 T T( z ) h x h1 , h 2 , h 3 x nhờ thay phép tính xấp xỉ Galerkin (1.48) vào mô hình (1.47). T Hệ có hai tín hiệu vào u (,) u1 u 2 là các cường độ dòng nhiệt được đưa vào mặt dưới và mặt trên của vật nung theo chiều z . 2. Thành phần thứ hai là một khâu quan hệ mờ Mamdani để xác định c( T ), ( T ) từ đầu ra T . Khâu quan hệ mờ Mamdani này có các thành phần chi tiết như sau: Khối mờ hóa cho ở hình 2.6 của tín hiệu đầu vào T có tên gọi các tập mờ lần lượt là Tlj , j 1,2, ,9 cho ()T và Tci , i 1,2, ,12 cho c() T , có các tập mờ đầu ra ldj, c i tương ứng đều là hàm singleton: ldj [60 , 57.5 , 47.5 , 37.5 , 30 , 25 , 27 , 28 , 35] (1.52) ci [0.4 , 0.5 , 0.5, 0.6 , 0.7 , 1.8 , 1.8 , 0.6 , 1 , 1 , 0.6 , 0.8] Luật hợp thành: Nếu T Tlj thì ldj với j 1,2, ,9 . (1.53) Nếu T Tci thì c ci với i 1,2, ,12 . (1.54) Giải mờ theo phương pháp điểm trọng tâm. 8 Hình 2.6 và hình 2.7 là các hàm liên thuộc biểu diễn giá trị mờ của các biến ngôn ngữ vào, ra gồm T và c( T ), ( T ) cho mô hình trạng thái (1.51) tương ứng với vật nung có các tham số vật lý lấy từ tài liệu [14,16]. Hình 2.8 là đồ thị quan hệ vào ra của khối quan hệ mờ này và đó cũng là đồ thị biểu diễn hai hàm c( T ), ( T ) phụ thuộc nhiệt độ trong vật nung. Hình 2.5: Cấu trúc mô hình Galerkin-Mờ Hình 2.6: Mờ hóa tín hiệu vào Hình 2.7: Mờ hóa tín hiệu ra Hình 2.8: Đồ thị biểu diễn sự phụ thuộc của (T ), c ( T ) vào nhiệt độ thể hiện qua khâu quan hệ mờ. Về mặt kim loại học, sự biến đổi lớn của các hệ số (T ), c ( T ) xảy ra trong vùng nhiệt độ từ 800 1200[K ] thể hiện trên hình 2.8 đã phản ánh đúng bản chất vật lý của quá trình biến đổi cấu trúc vật liệu nung theo nhiệt độ, tức là do sự thay 9 đổi về cấu trúc vật liệu thép các bon từ trạng thái ferrit sang trạng thái austenit trong quá trình luyện thép [5,12,..,17]. 2.3 Đánh giá chất lượng mô hình Galerkin-Mờ mô tả trường nhiệt độ trong vật nung dày Luận án đánh giá chất lượng mô hình Galerkin-Mờ đề xuất được thực hiện trên cơ sở so sánh với những mô hình thực nghiệm đã được kiểm chứng qua thực tế. Đó là những mô hình đã được trình bày ở mục 2.1.3 và 2.3.4 trong quyển luận án gồm: mô hình đẳng nhiệt dạng lưới sai phân, mô hình đẳng nhiệt cân bằng năng lượng và mô hình vật lý được xây dựng bởi Simscape của Matlab. Mô phỏng cho vật nung dày là thép tấm (0,1%C) có chiều dày 0,5 [m], khối lượng riêng 7000[kg / m3 ], hệ số bức xạ của phần tường lò bao quanh vật nung w 0,7 và w 0,7 . Vật nung được gia nhiệt với nguồn nhiệt bức xạ có nhiệt độ Tw ( t ) 1600 K và Tw ( t ) 300 K . Giả thiết nhiệt độ ban đầu trong toàn bộ vật nung là 300K . Các kết quả mô phỏng so sánh mô hình Galerkin-Mờ và các mô hình thể hiện ở các hình 2.9 ÷2.15. Hình 2.9: So sánh nhiệt độ tâm vật Hình 2.10: So sánh phân bố trường nung khi sử dụng các mô hình khác nhiệt độ của mô hình Galerkin-Mờ và nhau. mô hình lưới sai phân. Từ các mô hình và kết quả mô phỏng trên hình 2.9 đến hình 2.15 ta nhận thấy, nhiệt độ tại lớp vật nung tùy ý có thể được tính toán và thể hiện bởi các mô hình đã đề xuất. Tuy nhiên với các phương pháp xây dựng mô hình thực nghiệm ta phải tính toán lại nếu muốn chia số lớp vật nung ít hơn hay nhiều hơn, còn với mô hình Galerkin-Mờ ta chỉ cần thay đổi giá trị của biến z trong T() z và (1.48) thể hiện khả năng biểu diễn đơn giản nhiệt độ tại điểm bất kỳ bên trong vật nung của mô hình Galerkin-Mờ. Bên cạnh đó, đồ thị phân bố nhiệt độ tâm vật nung thu được của các mô hình cũng đã phản ánh đúng logic bản chất vật lý của vật nung dầy, nhiệt độ tại các vị trí không gian xa nguồn nhiệt ngày càng nhỏ dần, chênh lệch về 10 nhiệt độ giữa mặt trên và mặt dưới của vật nung giảm dần theo thời gian và có xu hướng ổn định khi giữ tác động đầu vào là cường độ dòng nhiệt không thay đổi. Nhiệt độ tâm vật nung thể hiện rõ tính phi tuyến khi phụ thuộc vào các tham số nhiệt vật lý (T ), c ( T ) của vật liệu, mặc dù có sự sai khác như ở hình 2.15 do nguyên nhân trong mô hình Galerkin-Mờ thì các thông số nhiệt vật lý của vật nung như hệ số dẫn nhiệt và nhiệt dung riêng (T ), c ( T ) phụ thuộc vào nhiệt độ như ở hình 2.8, còn khi xây dựng mô hình vật lý từ Simscape thì các đại lượng trên là hằng số được tra từ tài liệu tham khảo [5]. Hình 2.13: Khối vật nung được xây Hình 2.15: Khảo sát nhiệt độ vật nung dựng với Toolbox Simscape. của mô hình vật lý Simscape và mô hình Galerkin-Mờ đề xuất. Để khắc phục được sai số giữa mô hình lò nung xây dựng với Simscape và mô hình Galerkin-Mờ đề xuất, ta cần xây dựng mô hình vật lý của vật nung có tham số phụ thuộc nhiệt độ hoặc phải hiệu chỉnh công cụ mờ trong việc xây dựng mối liên hệ phụ thuộc của (T ), c ( T ) vào nhiệt độ. Nói cách khác, việc xác định các tham số nhiệt vật lý của vật liệu kim loại còn phụ thuộc vào nhiều yếu tố khác, đây cũng là một lĩnh vực rất khó đang được các nhà nghiên cứu tập trung tìm hiểu trong thời gian gần đây [38,49,51]. Do đó, luận án sẽ hướng tới giải pháp bổ sung thêm cho bộ điều khiển đã giới thiệu ở hình 1.2 có khả năng bù được sai lệch này thay vì chỉnh định thích nghi cơ cấu mờ. KẾT LUẬN CHƯƠNG 2 Như vậy nội dung chương 2 đã trình bày đóng góp chính thứ nhất của luận án đó là: 1. Xây dựng được khâu chỉnh định mờ hai tham số c( T ), ( T ) thay vì phải xác định giá trị trung bình c , trong không gian của vật nung. Điều này cho phép khi kết hợp cùng với mô hình tách biến Galerkin ta sẽ có ngay được một mô hình toán tường minh, mà luận án đặt tên gọi là mô hình Galerkin-Mờ, dưới dạng vòng kín (hình 2.5), khá tiện lợi cho công việc xây dựng bộ điều khiển sau này. 11 Cấu trúc khâu quan hệ mờ bổ sung vào mô hình tách biến Galerkin đã được thiết kế dựa trên đặc tính vật liệu nung lấy từ ở tài liệu [14,16,17]. Đối với các vật liệu nung có chất liệu vật lý khác, một cách tương tự ta có thể thiết kế được bộ quan hệ mờ tương ứng dựa vào tham số đặc tính vật lý truyền nhiệt của vật nung đó. 2. Đã tiến hành mô phỏng đánh giá chất lượng mô hình Galerkin-Mờ trên cơ sở so sánh với một số mô hình thực nghiệm và mô hình vật lý Simscape. Các kết quả ở các hình 2.9, hình 2.11, hình 2.15 và hình 2.16, đều đi tới chung một khẳng định về ưu điểm của mô hình Galerkin-Mờ đề xuất này. CHƯƠNG 3: ĐIỀU KHIỂN QUÁ TRÌNH NUNG VỚI BỘ ĐIỀU KHIỂN LQR CÓ RÀNG BUỘC TRƯỢT DỌC TRÊN TRỤC THỜI GIAN Từ mô hình Galerkin-Mờ có dạng song tuyến được đề xuất ở chương 2. Tác giả đã ứng dụng thuật toán mô hình nội với bộ điều khiển vòng ngoài theo nguyên lý tối ưu trượt dọc trục thời gian để điều khiển trường nhiệt độ trong vật nung bám theo quỹ đạo đặt cho trước. Thuật toán đề xuất có xét đến ảnh hưởng của nhiễu đầu vào dạng xung, nhiễu đầu ra của mô hình và có khả năng thỏa mãn điều kiện ràng buộc của hệ thống. Mô phỏng kiểm chứng chất lượng hệ thống điều khiển với bộ điều khiển đề xuất trên mô hình vật lý được xây dựng bởi Toolbox Simscape của Matlab. 3.1 Tổng quan về các phương pháp điều khiển Các phương pháp điều khiển hiện nay đều tập trung vào điều khiển nhiệt độ bề mặt vật nung theo một quỹ đạo cho trước, tức là cung cấp cho phương trình truyền nhiệt (1.47) giá trị biên T(,) S t . Các phương pháp này được chia thành hai loại chính là điều khiển hở và điều khiển vòng kín. Đặc điểm chung của nhóm phương pháp vòng kín, với ưu điểm hơn hẳn sơ đồ điều khiển hở, là khi được triển khai thực tế chúng đều có dạng nối tầng (cascade) và ứng dụng được khi các quỹ đạo đặt nhiệt độ vật nung biến đổi liên tục theo thời gian. Nguyên lý làm việc của nhóm phương pháp này là căn cứ theo sai lệch tín hiệu nhiệt độ có thực của vật nung so với nhiệt độ đặt mong muốn để hiệu chỉnh lại năng lượng cung cấp cho vật nung. Cấu trúc điều khiển lò nung là hở hay kín thì chúng cũng đều có điểm chung trên cơ sở phân lớp vật nung với quỹ đạo tham chiếu đặt trước của nhiệt độ các vật nung có thể được tính trực tuyến (online) hoặc định trước và lưu trữ như trong các công bố [27,28,39]. 3.2 Đề xuất cấu trúc điều khiển Luận án đề xuất về cấu trúc và phương pháp điều khiển có thể thích ứng được với mô hình truyền nhiệt trong vật nung dưới dạng phương trình PDE, nhằm điều khiển trường nhiệt độ bên trong vật nung T(,) V t thay vì thay đổi nhiệt độ bề mặt vật nung T(,) S t . Cấu trúc hệ thống điều khiển đề xuất như hình 3.2 12 Hình 3.2: Đề xuất sử dụng cấu trúc điều khiển mô hình nội để điều khiển quá trình truyền nhiệt trong vật nung dày. Sau khi phân tích và khẳng định được tính điều khiển được của cấu trúc mô hình nội đề xuất và phương pháp quan sát trạng thái cho mô hình đó dựa trên các công cụ giải tích. Luận án trình bày giải pháp của NCS để hiện thực hóa cấu trúc điều khiển. Cụ thể, luận án đề xuất bộ điều khiển đảm bảo chất lượng bám theo giá trị đặt mong muốn cho hệ song tuyến có tham số mô hình bất định, để từ đó có thể áp dụng điều khiển được trường nhiệt độ trong vật nung đi theo quỹ đạo mong muốn. 3.2.1 Tư tưởng thiết kế bộ điều khiển Luận án sẽ sử dụng mô hình Galerkin-Mờ một đầu vào (1.55) để xây dựng bộ điều khiển lò-vật nung. Để đảm bảo được chất lượng điều khiển một cách bền vững với sai lệch mô hình, luận án sẽ định hướng thiết kế bộ điều khiển trên nền tối ưu hóa, theo nghĩa sẽ cực tiểu hóa tổng bình phương sai lệch bám tín hiệu đặt. Định hướng này sẽ góp phần đảm bảo được tính bền vững của hệ thống, vì trong sai lệch đầu ra đó có chứa luôn cả thành phần sai lệch mô hình. Bộ điều khiển cực tiểu hóa sai lệch đầu ra được sử dụng ở đây là bộ điều khiển LQR. Việc tuyến tính hóa mô hình (1.55) xung quanh điểm thời gian hiện tại tk nên mô hình tuyến tính thu được sẽ phụ thuộc tk . Do đó, bộ điều khiển LQR tổng hợp được cũng phụ thuộc tk . Bởi vậy luận án đặt tên gọi cho bộ điều khiển tối ưu này là bộ điều khiển LQR có tham số biến đổi trượt dọc trên trục thời gian. Tư tưởng thiết kế bộ điều khiển LQR ở trên không phải là đề xuất của NCS. Nó đã được trình bày trong các tài liệu [3,4,..,54], và đã được cài đặt để điều khiển nhiều đối tượng phi tuyến công nghiệp khác nhau [52,55,56]. Đóng góp của luận án ở đây là đã cài đặt được tư tưởng thiết kế đã có này cho đối tượng cụ thể là vật nung với mở rộng là tính bất định tham số của mô hình Galerkin-Mờ (1.55), và điều khiển quá trình phân bố trường nhiệt độ trong vật nung. Ngoài ra, trên cơ sở phần chứng minh đã có từ tài liệu [52] và công bố [2] của tác giả sau khi bổ sung thêm giả thiết, luận án cũng đã chứng minh được tính bám ổn định tiệm cận của bộ điều khiển thu được này. Các kết quả đó đã được NCS công bố một phần ở công trình khoa học số [2]. 13 Hình 3.4: Minh họa nguyên lý thiết kế bộ điều khiển LQR có tham số biến đổi trượt dọc trên trục thời gian. Mô hình Galerkin-Mờ một đầu vào (1.55) là trường hợp riêng của các mô hình song tuyến có tham số phụ thuộc trạng thái và tín hiệu ra như sau: x A(,)(,) x y x B x y u (2.26) y C() x x T T trong đó: x x1, , xn là vector các biến trạng thái, u u1, , um là T vector các tín hiệu điều khiển và y y1, , yr là vector các tín hiệu đầu ra của hệ. Các ma trận A( x , y ), B ( x , y ) và C() x của mô hình (2.26) được giả thiết là những hàm liên tục theo đối số của chúng. Giả thiết tiếp là tại thời điểm hiện tại tk (hình 3.4), tất cả các biến trạng thái x() tk , đầu ra của hệ y() tk là đo được, khi đó, từ tính liên tục của A( x , y ), B ( x , y ) và C() x thì trong khoảng thời gian rất nhỏ sau đó [,)tk t k 1 với tk 1 t k k và k 0 là một hằng số dương đủ nhỏ, mô hình song tuyến (2.26) sẽ xấp xỉ được bởi mô hình LTI: x Ak x B k u Hk : , tk t t k 1 t k k (2.27) y Ck x với Ak Axtyt (),(), k k B k Bxtyt (),(), k k C k Cxt () k (2.28) Mô hình LTI Hk (2.27) sẽ được sử dụng để thiết kế bộ điều khiển LQR k để điều khiển đối tượng (2.26) trong khoảng thời gian tk 1 t t k 2 . Bộ điều khiển k này được thiết kế với mục đích làm cho đầu ra y của hệ LTI Hk bám theo được giá trị đặt hằng số wk w() tk khit . Ở khoảng thời gian tiếp theo là [,)tk 1 t k 2 ta sẽ lại có bộ điều khiển LQR kế tiếp là k 1 để điều khiển đối tượng song tuyến (2.26) trong khoảng thời gian [,)tk 2 t k 3 . Như vậy bộ điều khiển cuối cùng thu được trên cơ sở hợp nhất: k khi t [ tk 1 , t k 2 ), k 0,1, (2.29) 14 cũng sẽ vẫn là bộ điều khiển LQR, song có tham số thay đổi theo từng khoảng thời gian [,)tk 1 t k 2 , nên được gọi là bộ điều khiển LQR có tham số biến đổi dọc trục thời gian, hay bộ điều khiển LQR không dừng. 3.2.2 Ước lượng nhiễu và các thành phần bất định Luận án phát triển nguyên lý thiết kế bộ điều khiển LQR có tham số biến đổi theo thời gian, để áp dụng được khi hệ song tuyến có nhiễu v, d ( t ), n ( t ) tác động và có thêm thành phần bất định tham số mô hình , cụ thể: x Axy( , ) AB xBxy ( , ) ( udt ( )) vt ( ) (2.30) y C( x ) C x n ( t ). Mô hình (2.30) được viết lại: x A(,)(,)() x y x B x y u t y C()() x x t với (t ) AB x ( u d ( t )) v ( t ) và ()()t C x n t là những đại lượng không xác định được của mô hình. Giả thiết hai đại lượng này là liên tục và biến đổi không nhanh theo thời gian thì ta có thể xấp xỉ được chúng tại thời điểm tk thông qua các giá trị đã có trước đó của hệ thống, gồm x, u , y : k 1 k 1 k 1 ()()(,)(,)t xt Axyx Bxyu k k k k 1k 1 k 1 k 1 k 1 k 1 (2.31) ()()t y C x x k k k k k trong đó x() tk được ước lượng bởi x()() tk xk x k 1 k 1 (2.32) và trạng thái x() t không lẫn nhiễu cũng được giả thiết là đo được. Như vậy, trên toàn bộ trục thời gian, mô hình song tuyến bất định (2.30) là xấp xỉ được bởi vô số (đếm được) các mô hình tuyến tính tiền định / Hk , k 0,1, có dạng: x A x B u / k k k Hk : có tk t t k 1 t k k . (2.34) y C x k k Từng mô hình LTI H / với , được ước lượng theo (2.31), sẽ được luận án sử k k k dụng để thiết kế bộ điều khiển LQR k thay vì mô hình LTI ban đầu là Hk . Đây cũng là một đóng góp của luận án theo hướng mở rộng phương pháp thiết kế đã có trong các tài liệu [4,8,..,56], sao cho bộ điều khiển LQR thu được còn áp dụng được cho cả những hệ song tuyến có tham số bất định như mô hình (2.30). 3.2.3 Thiết kế bộ điều khiển LQR có tham số biến đổi theo thời gian 15 Nhiệm vụ của bộ điều khiển với cấu trúc cho ở công thức (2.29), mà ta cần thiết kế, là phải làm cho đầu ra của hệ bất định tham số, có nhiễu tác động, mô tả ở (2.30), bám tiệm cận theo được quỹ đạo đặt w() t cho trước. Ta chuyển bài / toán điều khiển bám tiệm cận y()() t w tk cho hệ Hk thành bài toán điều khiển / ổn định. Do đó, cần xác định được những trạng thái xác lập của hệ Hk khi đã bám theo được giá trị đặt wk w() tk là hằng số. / Ký hiệu những giá trị xác lập của hệ Hk là xs [] k và us [] k thì ta có: 0 Ak x s [ k ] B k us [ k ] k w C x[]. k k k s k vì wk là hằng số trong toàn bộ khoảng thời gian điều khiển tk t của k . Suy ra: k ABABk k xs[][] k x s k k k FFk , k (2.35) w CCu[][] k u k k k k s s k xs [] k 1 k Fk , khi Fk khả nghịch. (2.36) u[] k w s k k / Vậy khi đã có các trạng thái xác lập của hệ Hk mô tả bởi (2.34) thì với ký hiệu: ()()[]t x t x k và ()()[]t u t u k bài toán điều khiển bám cho hệ k s k s / Hk được chuyển thành bài toán điều khiển ổn định hệ: AB . (2.37) kk k k k Để điều khiển ổn định hệ (2.37) sao cho có thêm được chất lượng bền vững với sai lệch mô hình, ta sẽ dùng một tiêu chuẩn tối ưu. Tiêu chuẩn tối ưu được luận án sử dụng là tích phân bình phương của hai quỹ đạo (t ), ( t ) trong toàn bộ k k khoảng thời gian còn lại [,]tk với hai ma trận đối xứng xác định dương QRk, k tùy chọn. TT J Q R dt min (2.38) k k k k k
File đính kèm:
 luan_an_nghien_cuu_xay_dung_mo_hinh_qua_trinh_truyen_nhiet_b.pdf
luan_an_nghien_cuu_xay_dung_mo_hinh_qua_trinh_truyen_nhiet_b.pdf

