Luận án Phát triển phương pháp phủ tuyến tính để kiểm tra tính Hurwitz chặt và ứng dụng vào thiết kế tham số tối ưu trong điều khiển hệ tuyến tính bất định

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
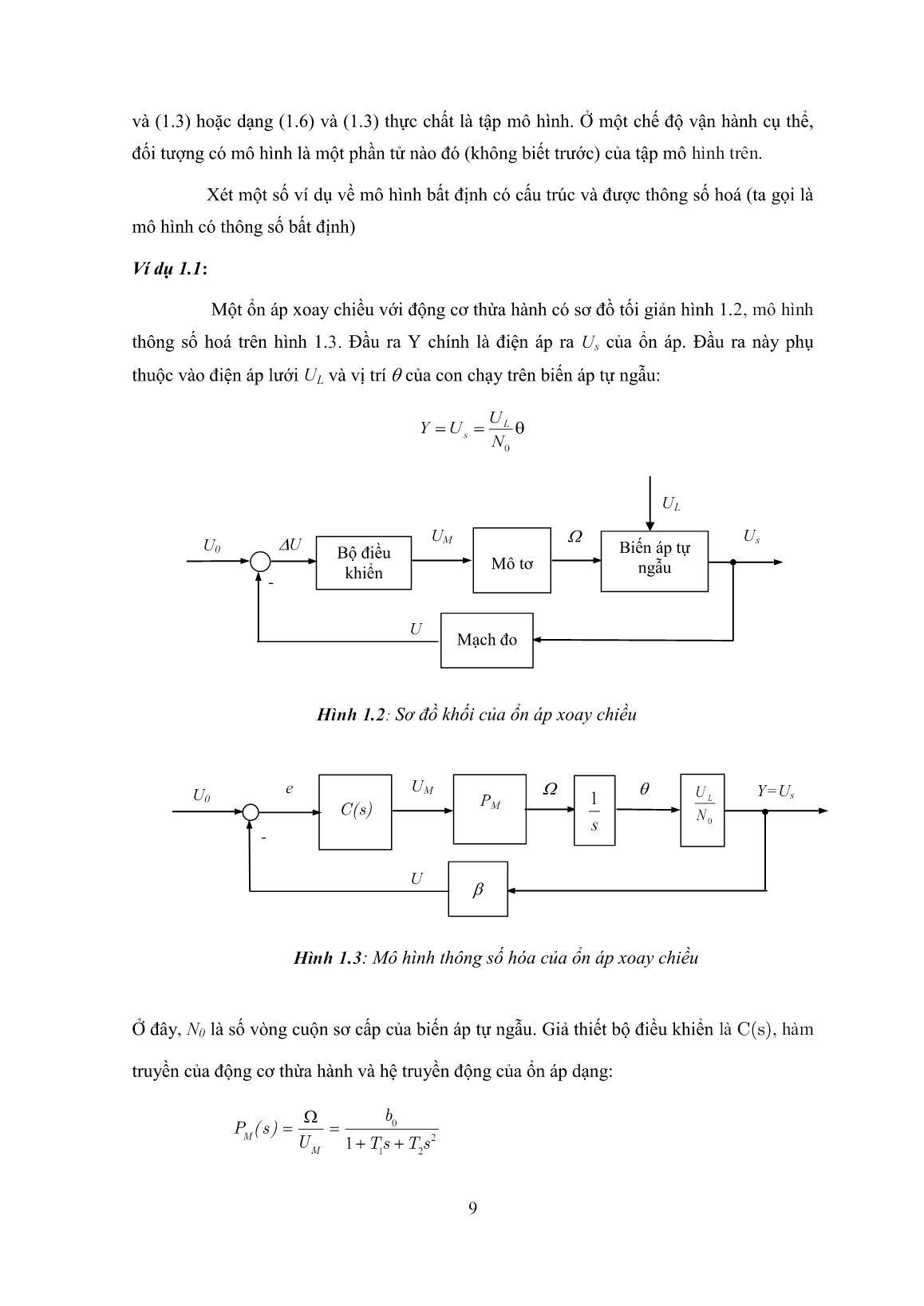
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Luận án Phát triển phương pháp phủ tuyến tính để kiểm tra tính Hurwitz chặt và ứng dụng vào thiết kế tham số tối ưu trong điều khiển hệ tuyến tính bất định", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Luận án Phát triển phương pháp phủ tuyến tính để kiểm tra tính Hurwitz chặt và ứng dụng vào thiết kế tham số tối ưu trong điều khiển hệ tuyến tính bất định

H 0 1 0 2 1 1 1 2 min 4 y1 2 y 2 , 4 y 1 2 y 2 , 4 y 1 2 y 2 , 4 y 1 2 y 2 min 16 , 1, 11, 2 16 y2 12 E q2 3 H G E q2 =2 G 8 12 22 Q Q 2 I K D q =1 H 2 4 D 11 21 T K Q Q 1 A q1 I 11 y q2 =0 B C Y B C 1 A 1 2 3 0 0 q1 =1 q1 =2 q1 =3 1 4 9 Hình 2.10: Minh họa tính phủ của tập H lên tập Y ở ví dụ 2.2 22 Hình 2.10 mô tả miền ảnh Y của Q với phép biến đổi y1 q 1, y 2 q 1 q 2 , cũng như các vj vj 11 miền ảnh Y, vj 1,2; j 1,2 của Q, vj 1,2; j 1,2 . Ví dụ Q là miền nằm trong hình chữ nhật có các đỉnh ABKI, có miền ảnh là Y 11 được bao bởi các đường có các điểm ABKI. Tập phủ tuyến tính H 11 của Y 11 là hình chữ nhật ABKT. 3) Dùng chương trình tính khi cho N tăng dần và những giá trị ban đầu khác nhau ta có kết quả như ở bảng, ta cũng thấy tính tiệm cận và tính non của MuN : N 1 10 102 103 104 105 106 48 -19 -12.16 -11.1196 -11.012 -11.0012 -11.00022 -11.0001 Dùng chương trình tính cực tiểu non MuN theo thuật toán 1, có tính đến sai số cho 4 phép, cụ thể nếu chọn hệ số tăng A0 10, 0, 1, 2, ..., sai số cho phép cp 10 . Bảng kết quả tính khi tăng N cho ta kết quả MuN cũng tăng dần, cũng nhỏ dần lại. Ở lần tính thứ 6 (N 105 ) có so với lần tính thứ 5 (N 104 ) là: 54 5 6 9.1 10 cp 10 nếu sai số cho phép cp 10 thì ở bước tính thứ 7 (N 10 ) so 65 với bước tính thứ 6 sẽ cho sai số tương đối là: 9 10 cp 10 . Chương trình tính sẽ dừng ở lần tính thứ 7. 2.2.3 Sử dụng trị cực tiểu non để kiểm tra tính Hurwitz chặt của đa thức có thông số bất định 2.2.3.1 Trình tự các bƣớc kiểm tra tính Hurwitz chặt Với thuật toán xác định trị cực tiểu non của một đa thức có hệ số là hàm chứa thông số bất định vừa được đề xuất, ta cũng có thể kiểm tra được tính Hurwitz chặt của đa thức đặc tính: n (,)s q a01 () q a () q s an () q s (2.59) cho ở công thức (2.4) hoặc (2.7). Đây là đa thức có các hệ số a(), q a (), q , a () q đều (,)sq 01 n là những hàm số phụ thuộc thông số bất định qQ RL . Không mất tính tổng quát ta luôn giả sử được rằng đa thức này có tất cả các hệ số là cùng dấu và khác không với mọi , vì nếu điều đó không xảy ra ta có thể dựa vào tiêu chuẩn Routh-Hurwitz để kết luận rằng không phải là đa thức Hurwitz. Thêm nữa, cũng không mất tính tổng quát, ta giả sử tiếp chúng đều có giá trị là số dương. Khi đó trình tự các bước kiểm tra tính Hurwitz chặt của đa thức sẽ gồm các bước như sau: Dựa vào của hệ, ta lập bảng Routh ta xác định được n 1 các hàm gk (), q k 1,2, , n 1. Sử dụng phương pháp tính trị cực tiểu non MkuN , k 1,2, , n 1 của tất cả các hàm trên gk (), q q Q , k 1,2, , n 1. Để giảm khối lượng tính toán, trong quá trình tính nếu có một giá trị MkuN ứng với một hàm gqk thỏa mãn MkuN 0 thì dừng không cần tính đối với giá trị nữa khi các giá trị N tăng. MuN 49 Nếu có MkkuN 0, thì theo tiêu chuẩn Routh-Hurwitz, đa thức sẽ là Hurwitz chặt. Nếu có N là đủ lớn và tồn tại ít nhất một chỉ số k mà có MkuN 0 thì không phải là Hurwitz chặt. 2.2.3.2 Một số ví dụ số để minh họa Đê minh họa khả năng ứng dụng phương pháp tìm trị cực tiểu non vào bài toán kiểm tra tính ổn định bền vững, tức là kiểm tra tính Hurwitz chặt của đa thức (,)sq , và so sánh kết quả khi áp dụng các phương pháp đã có khác, trong mục này luận án sẽ đưa ra một số ví số sau đây. Ví dụ 2.3: Ở ví dụ này ta sẽ kiểm tra tính Hurwitz chặt của đa thức: 2 (s , q ) q1 2 q 2 2 q 2 1 s 2 q 1 q 2 4 s (VD2.3-1) T với q q12 , q và tập ràng buộc (hình 2.7): 2 Q q R 0.5 q12 2 , 0.3 q 0.3 (VD2.3-2) theo hai phương pháp, phương pháp thứ nhất sử dụng định lý đa thức cạnh [8, 17, 65] và phương pháp thứ hai là xác định trị cực tiểu non vừa đề xuất, để so sánh. q2 (,)sq 0.3 (4) (3) q -0.5 2 1 0 (1) -0.3 (2) Hình 2.11: Minh họa ví dụ 2.3 1) Trước tiên ta sẽ áp dụng phương pháp đa thức cạnh. Ứng với mỗi cạnh của hộp Q ta có 2 đa thức cạnh, ví dụ với cạnh ứng với 2 đỉnh (1) và đỉnh (2) trên hình 2.11 ta có: (1) (2) 12 s, q 1 s , q (VD2.3-3) s, q(2) 1 s , q (1) 21 50 (1) (2) với thông số nằm trong khoảng 01 . Gọi 12 s,,, q s q là các đa thức đặc trưng ứng với đỉnh (1) có qq12 0.5, 0.3 và đỉnh (2) có qq12 2, 0.3 ta tính được: (1) 2 1 s, q 2.1 0.7 s 3.3 s (2) 2 2 s, q 3.4 0.7 s 9.7 s Thay vào (VD2.3-3) ta được: (,)sq 22 12 (s , ) 2.1 0.7 s 3.3 s (1 ) 3.4 0.7 s 9.7 s (s , ) 3.4 0.7 s 9.7 s22 (1 ) 2.1 0.7 s 3.3 s 21 hay 2 12 (s , ) 2.1 1.3 0.7 s (9.7 6.4 ) s 2 21(s , ) 2.1 1.3 0.7 s (3.3 6.4 ) s Tương tự lập được 23(,),s 32 (,), s 43 (,), s 34 (,), s 14 (,), s 41 (,) s , mỗi một đa thức cạnh ij s, là đa thức chỉ chứa một thông số [0,1] nên ta đưa về đa thức khoảng để xét ổn định. Ví dụ xét ổn định cho đa thức 12 s, ta đưa về đa thức khoảng: 2 12 s, 2.1 3.4 0.7 s 3.3 9.7 s Để xét ổn định cho đa thức khoảng này có thể dùng tiêu chuẩn Kharitonov ta được 4 đa thức sau (gọi là đa thức Kharitonov): 12 2.1 0.7ss 9.7 12 22 12 3.4 0.7ss 3.3 (VD2.3-4) 32 12 3.4 0.7ss 3.3 42 12 2.1 0.7ss 9.7 Cả 4 đa thức trên đều ổn định nên đa thức cạnh 12 s, ổn định. Tương tự như vậy xét tất cả các đa thức cạnh ij s, khác cũng ổn định. Như vậy đa thức (VD2.3-1) là ổn định bền vững trong tập (VD2.3-2). Ở đây với có cấu trúc tuyến tính và Q dạng hộp nên ta đưa về được 28L L đa thức cạnh và phải xét 32 đa thức Kharitonov (số đa thức Kharitonov tăng theo hàm mũ) không chứa thông số. 2) Nếu dùng phương pháp phủ tuyến tính để xét ổn định của hệ thống đã cho với các đa thức (VD2.3-1), (VD2.3-2). Để các thông số bất định có giá trị không âm ta thực hiện phép đổi biến số như sau: 51 // q1 q 1 0.5 q 1 q 1 0.5 (VD2.3-5) // q2 q 2 0.3 q 2 q 2 0.3 Với phép biến đổi (VD2.3-5) đa thức (VD2.3-1) trở thành: / / / / / / 2 (s , q ) 2.1 q1 2 q 2 q 2 0.7 s 3.3 2 q 1 q 2 s (VD2.3-6) / / / 2 a0()()() q a 1 q s a 2 q s khoảng biến thiên của các thông số bất định mới trong tập Q / là: //// (,)sq (VD2.3-7) Q q0 q12 2.5 , 0 q 0.6 Bài toán xét ổn định của (VD2.3-1) với ràng buộc (VD2.3-2) tương đương với bài toán xét ổn định của (VD2.3-6) với ràng buộc (VD2.3-7). Dùng tiêu chuẩn Routh để cho đa thức (VD2.3-6) ổn định ta phải có: g( q// ) a/// ( q ) (2.1 q 2 q ) 0 1 0 1 2 //// g2( q ) a 1 ( q ) (0,7 q 2 ) 0 (VD2.3-8) g q// a///// q q q q Q 3( ) 3 ( ) (3.3 2 1 2 ) 0 , Như vậy, để hệ ổn định với qQ// các bất đẳng thức sau phải được thỏa mãn: M min g ( q / ) 0 11uN / // 2 / / / với q Q q R 0 q 2.25 , 0 q 0.6 (VD2.3-9) M22uN min g ( q ) 0 12 M min g ( q / ) 0 33uN /// / / Ở đây g1( q ), g 2 ( q ), g 3 ( q ) là các hàm tuyến tính của q nên Y và Q trùng nhau. Bởi vậy ta có thể dễ dàng tìm được cực tiểu toàn thể của (VD2.3-9) nhờ phương pháp qui hoạch tuyến tính: // M1uN min 2.1 q 1 2 q 2 2.1 1 0 2 0.6 0.9 0 / Mq22uN min 0.7 0.7 1 0 0.7 0 // M3uN min 3.3 2 q 1 q 2 2 0 1 0.6 3.3 2.7 0 Vì các giá trị MMM1uN, 2 uN , 3 uN đều dương nên các bất đẳng thức (VD2.3-8) đều dương do đó đa thức của (VD2.3-1)) ổn định bền vững trong tập thông số (VD2.3- 2). Rõ ràng với trường hợp nL 2, 2 với đa thức bất định tuyến tính phương pháp phủ tuyến tính cho kết quả nhanh hơn phương pháp sử dụng đa thức cạnh. Ví dụ 2.4: Xét ổn định của hệ thống với phương trình đặc trưng có cấu trúc phi tuyến chứa một thông số bất định như sau: s q s4 s 3 q 2 s 2 q 2 s q 4 q 2 (,) 2 (2 3) (22)( 2 1) 52 với thông số bất định của q trong khoảng 0 q 0.9854 . Ở ví dụ này, phương pháp của Kharitonov và phương pháp đa thức cạnh không dùng được, ta sử dụng phương pháp phủ tuyến tính và dùng thuật toán 1 để tính các giá trị cực tiểu non của các ràng buộc xuất phát từ điều kiện cần và đủ của tiêu chuẩn ổn định Routh dưới đây: 2 g1( q ) 3 q 2 0 42 g2 ( q ) 4 q 3 q 1 0 42 g3( q ) q 2 q 1 0 có 0 là số thực dương nhỏ tùy ý. Áp dụng thuật toán đề xuất ta xác định được các giá trị MkuN như sau: N 1 10 102 103 104 M11uN min g ( q ) 2 2 2 2 2 M22uN min g ( q ) 2.7715 0.4119 0.0836 0.1358 0.141 M33uN min g ( q ) 0.942 0.3234 0.0363 0.0029 0.005 Với số khoảng chia là N 104 , các giá trị cực tiểu non của 3 ràng buộc đã dương, vậy ta kết luận được hệ thống đã ổn định với mọi giá trị của trong khoảng đã cho. Đối với bài toán kiểm tra ổn định, để cải thiện tốc độ tính toán ngoài các lưu ý về các giá trị ban đầu trong ví dụ này ta cần thêm điều kiện dừng khi giá trị nào đó dương (MkuN 0 ), trong trường hợp này thì tại bước tính đầu tiên khi N=1 giá trị M1uN 0 nên các bước tính sau ta không cần tính giá trịM1uN , tương tự ở bước tính thứ 3 khi N=100 giá trịM2uN 0 nên các bước tính sau ta không cần tính giá trịM2uN , như vậy ở bước tính thứ 3 và thứ 4 ta chỉ cần tính giá trịM3uN đến khi giá trịM3uN 0 ta dừng chương trình tính. Ví dụ 2.5: Xét hệ thống với phương trình đặc trưng có cấu trúc dạng đa tuyến tính (multilinear) chứa 5 thông số bất định T q q,q,q,q,q Q : 1 2 3 4 5 (,)()()()()sq aqs32 aqs aqsaq (VD2.5-1) 0 1 2 3 Với các hệ số: a0( q ) 1, a 1 ( q ) 7.182 q 1 q 4 0.3795 q 5 , a2( q ) 2.181 0.32 q 1 19.231 q 2 0.00077 q 3 6.862 q 4 0.1208 q 5 q1 q 4 q 2 q 3 0.8795 q 2 q 5 0.3795 q 4 q 5 a3( q ) 0.017 22.031 q 2 0.000523 q 5 0.6795 q 2 q 5 Tập bất định thông số qQ có dạng: 53 5 0 qq12 0.0182, 0.000772 3.3, q Q q R (VD2.5-2) 0 q3 0.00007, 0 q 4 0.0001, 0 q 5 0.3 Dùng tiêu chuẩn Routh để xét điều kiện cần và đủ ổn định hệ thống có đa thức ở dạng multilinear (VD2.5-1) ta đưa đến: g1( q ) (7.182 ) q 1 q 4 0.3795 q 5 0 22 g2( q ) (15.6811 ) 4.4793 q 1 116.086 q 2 51.4639 q 4 1.6955 q 5 0.32 q 1 6.862 q 4 0.0458q2 19.231 q q 0.00077 q q 14.364 q q 0.2422 q q 5 1 2 1 3 1 4 1 5 7.182q2 q 3 19.231 q 2 q 4 12.9352 q 2 q 5 0.00077q3 q 4 0.000292 q 3 q 5 5.4505 q 4 q 5 qqq qqq qqqqqqq2 2 qq 2 qq 2 123 0.759 145 0.3795 2351414 0.3338 25 0.3795 45 0 g3( q ) (0.017 ) 22.031 q 2 0.000523 q 5 0.6795 q 2 q 5 0 Áp dụng thuật toán 1 đã đề nghị ta xác đinh được các giá trị MkuN ở bảng sau: N 1 10 102 103 104 M11uN min g ( q ) 7.04984 7.1103 7.122 7.1231 7.1233 M22uN min g ( q ) 1.2204 15.5713 15.7633 15.7701 15.7707 M33uN min g ( q ) 0.67285 0.0067489 0.0000624 0.0000069 0.0000069 Với số khoảng chia N=1 các giá trị MM12uN, uN đều dương, nên không cần tính tiếp 3 nữa, chỉ cần tăng N và tính với giá trị M3uN và ở giá trị N 10 thì M3uN đã dương, nên ta kết luận hệ thống đã thỏa mãn chặt điều kiện cần và đủ của ổn định bền vững. Ví dụ 2.6: Xét hệ thống có sơ đồ cấu trúc hình 2.1, có bộ điều khiển Cs() và đối tượng chứa 2 thông số bất định P(,) s q có cấu trúc bất định dạng polynomic (phi tuyến có nhiều thông số bất định) như sau: 1,8 q q C( s ) , P ( s , q ) 1 , q 1 2 2,4ss 0,5 16 q q2 q s q 2 1 2 2 Miền ràng buộc Q của thông số bất định là tập: 2 Q q R 0.8 q12 5 , 0.32 q 10 Từ sơ đồ cấu trúc hệ thống kín, ta xác định được phương trình đặc trưng của hệ thống kín: (sq , ) 3 0.5 q 0.5 qqs2 3 14.9 2.4 q 2.4 qqs 2 2 2.4 sq 1.8 2 1 2 2 1 2 1 Đây là đa thức đặc trưng dạng polynomic. Dùng tiêu chuẩn Routh cho hệ kín ta sẽ có điều kiện cần và đủ để hệ thống kín trên sẽ ổn định bền vững là: 54 g( q ) 3 0.5 q 0.5 q2 q 0 1 2 1 2 2 g2( q ) 14.9 2.4 q 2 2.4 q 1 q 2 0 23 g3( q ) 5.4 q 1 5.76 q 2 0.9 q 1 q 2 5.76 q 1 q 2 0.9 q 1 q 2 0 g41( q ) 1.8 q 0 có là số thực dương nhỏ tùy ý. Do các thông số bất định qq12, đều dương nên các hàm g1( q ), g 2 ( q ), g 4 ( q ) đều dương nên0 ta chỉ cần xác định gq3( ) 0 là hệ ổn định bền vững. Áp dụng thuật toán đã đề nghị ta xác đinh được các giá trị ở bảng: N 1 10 102 103 104 105 M min g ( q ) 33uN 1169.6 57.7363 0.1521 0.0053 0.0083 0.0096 4 Với số khoảng chia là N 10 , giá trị cực tiểu non của M3uN 0.0083 là số dương, nên ta kết luận hệ thống đã cho ổn định bền vững với mọi thông số bất định trên. Nhận xét Bằng phương pháp phủ tuyến tính thông qua thuật toán đề xuất, ta có thể giải quyết được bài toán có cấu trúc bất định ở dạng phức tạp như (multilinear) ở ví dụ 2.5, có cấu trúc dạng phi tuyến hoặc dạng polynomic như ví dụ 2.6, phương pháp này kiểm tra sự thỏa mãn chặt điều kiện ổn định bền vững. 2.2.4 Ứng dụng của trị cực tiểu non giải bài toán tối ƣu để kiểm tra điều kiện ổn định bền vững gắn với một số chất lƣợng khác Trị cực tiểu non không những dùng để kiểm tra ổn định bền vững mà còn có thể gắn thêm một số chỉ tiêu chất lượng khác bằng cách đưa về bài toán tối ưu. Ở đó các điều kiện ổn định bền vững được kể đến dưới dạng ràng buộc và một số chỉ tiêu chất lượng thường gắn với ổn định được thể hiện theo hàm mục tiêu và một số ràng buộc khác. Nghiệm của bài toán tối ưu tìm được mang thông tin về tính ổn định bền vững và tối ưu một chất lượng nào đó , ví dụ hệ số tắt nhanh nhất của quá trình quá độ, hoặc dải bất định của một thông số bất định nào đó rộng nhất. Dưới đây là một số ví dụ cho ý tưởng đã nêu ở trên. 2.2.4.1 Xác định dải biến thiên tốc độ rộng nhất Bài toán quan tâm là hệ thống cơ khí đã được Siljack trình bày có mô hình thông số bất định như ở (1-78) trong [63], với vận tốc góc được coi là thông số bất định. 55 Bằng cách phân rã (decomposition) kết hợp với phương pháp dùng hàm Lyapunov, Siljak đã tìm được khoảng biến thiên rộng nhất của là 0 0.05 để hệ ổn định bền vững. Sau đó, Yedavalli [57] đã xét lại ví dụ này bằng phương pháp áp đặt điểm cực và sử dụng phép chuyển đổi ma trận trạng thái để xét ràng buộc thông qua độ ổn định của đối tượng chuẩn. Qua một số lần cải tiến đã mở rộng dần khoảng biến thiên thông số bất định từ 0 0.1937 [56] lên đến khoảng rộng nhất là 0 0.3339 [57]. Ở đây, NCS cũng xét lại ví dụ này và dùng bài toán tối ưu đã trình bày ở trên để giải quyết bài toán. Ký hiệu vận tốc góc q là thông số bất định, hệ thống cơ khí nói trên có đa thức đặc trưng như sau: 4 3 2 2 2 4 2 (,)s q s 2 s (2 q 3) s (22)( q s q 2 q 1) (2.60) Khi đó bài toán xác định giới hạn vận tốc góc tối đa cho phép để hệ thống ổn định bền vững được đưa về bài toán tối ưu như sau: f( x ) x min 2 g1( q ) 2 3 q 0 24 (2.61) g2 ( q ) 1 3 q 4 q 0 24 g3 ( q ) 1 2 q q 0 g4 ( q ) x 0 với tập bất định: Q q R 0 q x Để dải biến thiên của thông số bất định q là lớn nhất ta chọn xq max max 0. khi đó hàm mục tiêu sẽ là: f( x ) x min . với các ràng buộc x 0 và g1( q ), g 2 ( q ), g 3 ( q ) đều dương xuất phát từ điều kiện ổn định của đa thức đặc trưng (2.60) theo tiêu chuẩn Routh, là một số dương rất nhỏ. Trong các ví dụ ta thống nhất chọn 10 6 . Giải bài toán tối ưu (2.61) nhờ phương pháp trị cực tiểu non ta tìm được nghiệm: N 10 100 103 104 x 0.4895 0.9045 0.9505 0.9892 max Như vậy ta đã tìm được dải bất định là vận tốc góc 0 qq max max 0.9892 rộng hơn so với kết quả mà Siljack và Yedavalli tìm được. 2.2.4.2 Ổn định với hệ số tắt nhanh nhất Xét hệ có phương trình đặc tính: 56 3 2 2 (,)s q s (6 q1 q 2 ) s (6 q 1 )(5 s q 2 ) (2.62) 2 Q q R 0 q12 0.5, 0 q 4 Theo tiêu chuẩn ổn định hàm mũ, để thỏa mãn yêu cầu quá trình quá độ tắt nhanh nhất thì phải có số mũ tắt 0 lớn nhất, hay x nhỏ nhất, như vậy hàm mục tiêu được chọn ở đây sẽ là f( x ) x min . Để hệ thống ổn định với số mũ tắt α thì đa thức (,,)sq dạng polynomic sau phải ổn định với qQ. (,,)s x q s3 (63 x q 2 q )(6123 s 2 x x 2 q 2 xq 2 q ) s ss 1 2 1 1 2 (2.63) 2 3 2 2 (5 6x 6 x x xq1 q 2 x q 1 q 2 ) Dùng tiêu chuẩn Routh xét ổn định cho đa thức (2.63) ta lập được bài toán với 4 ràng buộc cho hàm mục tiêu có chứa thông số bất định dưới đây: f( x ) x min 2 g1( x , q ) (6 3 x ) q 1 q 2 0 23 g2( x , q ) (31 84 x 48 x 8 x ) (6 2 x ) q 1 q 2 2 2 3 4 2 (6 24x 8 x ) q1 q 2 q 1 q 2 2 xq 1 q 2 0 (2.64) 2 3 2 2 gxq3( , ) (5 6 xxx 6 ) xqqxqq 1 2 1 2 0 g( x , q ) x 0 4 q Q q R2 0 q 0.5, 0 q 4 1 2 Giải bài toán tối ưu (2.64) nhờ dùng giá trị cực tiểu non ta thu được nghiệm của nó là xmin 0.4 . Điều này chứng tỏ hệ sẽ ổn định bền vững và có hệ số tắt nhanh nhất là max 0.4 . 2.2.4.3 Tính ổn định có tính bền vững cao nhất Phương pháp tìm cực tiểu non của luận án còn áp dụng được cho cả lớp bài toán điều khiển ổn định hệ bất định sao cho dải biến thiên thông số bất định của hệ là rộng nhất (được gọi là điều khiển ổn định có tính bền vững cao nhất). Để minh họa khẳng định trên, sau đây luận án sẽ trình bày một số ví dụ minh họa. Ví dụ 2.7: Xét lại hệ bất định (2.62) đã có ở mục trên nhưng với nhiệm vụ điều khiển bây giờ là cần phải tìm khoảng biến thiên thông số bất định lớn nhất của q để hệ thống ổn định bền vững với hệ số tắt là 0 0.2. Gọi khoảng biến thiên Q của qq12, là: Q q 0 q1 x 1 , 0 q 2 x 2 . (VD2.7-1) 57 22 Khi đó, theo chuẩn Euclide, để dải bất định (VD2.7-1) rộng nhất thì (xx12 ) max . 22 Vậy hàm mục tiêu tương ứng sẽ là f( x ) ( x12 x ) min . Kết hợp thêm điều kiện ổn định hàm mũ với 0 0.2 ta có bài toán tối ưu: 22 f( x ) ( x12 x ) min (VD2.7-2) với điều kiện ràng buộc dạng: g( x , q ) (5.4 ) q2 q 0 1 1 2 2 3 4 2 gxq2( , ) (16.056 ) 5.6 qq 1 2 1.52 qqqq 1 2 1 2 0.4 qq 1 2 0 2 g3( x , q ) (4.032 ) 0.2 q 1 q 2 0.04 q 1 q 2 0 (VD2.7-3) g x q x g x q x 4( , ) 1 0, 5 ( , ) 2 0 0 q x , 0 q x 1 1 2 2 Giải bài toán tối ưu (VD2.7-2), (VD2.7-3) nhờ trị cực tiểu non ta xác định được nghiệm của nó là x ( x12 , x ) (0.995 , 7.975). Vậy hệ sẽ ổn định bền vững với hệ số mũ tắt dần với khoảng biến thiên rộng nhất của thông số bất định là: Q q 0 q12 0.995 , 0 q 7.975 . Ví dụ 2.8: Đối tượng quan tâm là hệ tuyến tính có thông số bất định: z A() q z (VD2.8-1) trong đó ma trận trạng thái Aq() có các phần tử là hàm của vector các thông số bất định q : qq11 2 0 1 A( q ) 0 q 3 0 (VD2.8-2) 2 q1 1 q 2 1 q 1 4 cũng như tập ràng buộc Q của các thông số bất định là: 2 Q q R 0 q12 1.6 , 0 q 2.8 . Ký hiệu các giới hạn trên của qq12, lần lượt là x1 q 1 , x 2 q 2 thì để hệ tuyến tính (VD2.8-1), (VD2.8-2) ổn định, đa thức đặc trưng: (s , q ) det sI A ( q ) 32 s(92 qqs1 2 ) (2510 qqqqs 1 6 2 2 1 2 ) (2112 qqqq 1 7 2 4 1 2 ) phải là một đa thức Hurwitz, tức0 là 0.2nó phải có các đa thức ở cột đầu trong bảng Routh: g1( q ) 9 2 q 1 q 2 2 2 2 2 gq2( ) 204 128 qq 1212121212 72 36 qq 20 qqqqqq 6 2 4 g3( q ) 21 12 q 1 7 q 2 4 q 1 q 2 58 luôn dương với mọi 0 q1 x 1 , 0 q 2 x 2 . Như vậy bài toán xác định x1 q 1 , x 2 q 2 lớn nhất để hệ ổn định sẽ đồng nghĩa với việc xác định x12 , x thỏa mãn: 22 f( y ) ( x12 x ) min (VD2.8-3) với các điều kiện ràng buộc: g1( q ) 9 2 q 1 q 2 0 gq( ) 204 128 qqqqqqqqqq 72 36 202 6 2 2 2 4 2 0 2 1212121212 (VD2.8-4) g3( q ) 21 12 q 1 7 q 2 4 q 1 q 2 0 0 q1 x 1 , 0 q 2 x 2 Áp dụng trị cực tiểu non để tìm nghiệm bài toán tối ưu có ràng buộc (VD2.8-3), (VD2.8-4) nêu trên ta có nghiệm sau (phụ thuộc vào số lần chia khoảng N ) 2 3 3 3 4 5 N 10 10 10 2.10 5.10 10 10 x1 1.1 1.555 1.6450 1.655 1.682 1.699 1.732 x 2 2,1 2,556 2,898 2,9425 2,96 2,98 2,985 Vậy hệ sẽ ổn định bền vững với dải biến thiên rộng nhất cho các thông số bất định là: 0 qq12 1.732 , 0 2.985. Ví dụ 2.9: Xác định khoảng thông số bất định rộng nhất cho hệ tuyến tính bất định cho hệ thống biểu diễn dưới dạng phương trình trạng thái sao cho thỏa mãn hệ ổn định bền vững, với hệ số tắt của quá trình quá độ là 0.2 . Xét hệ tuyến tính bất định: q1 20 z A() q z z (VD2.9-1) 03q2 với khoảng dao động của hai thông số bất định là qq12, 0 q1 q 1 , 0 q 2 q 2 . Nhiệm vụ bài toán được đặt ra ở đây là phải xác định qq12, lớn nhất để hệ ổn định với tốc độ tắt dần là . Ở đây cá
File đính kèm:
 luan_an_phat_trien_phuong_phap_phu_tuyen_tinh_de_kiem_tra_ti.pdf
luan_an_phat_trien_phuong_phap_phu_tuyen_tinh_de_kiem_tra_ti.pdf Bia-LA Ttat.pdf
Bia-LA Ttat.pdf Bia-LA.pdf
Bia-LA.pdf Mucluc-LA.pdf
Mucluc-LA.pdf Tomtat-LA - 2017(chot).pdf
Tomtat-LA - 2017(chot).pdf TTin LA (Minh).pdf
TTin LA (Minh).pdf

