Luận án Thuật toán điều khiển thích nghi phi tuyến mới trên cơ sở mạng nơ ron nhân tạo cho robot công nghiệp

Trang 1

Trang 2

Trang 3

Trang 4
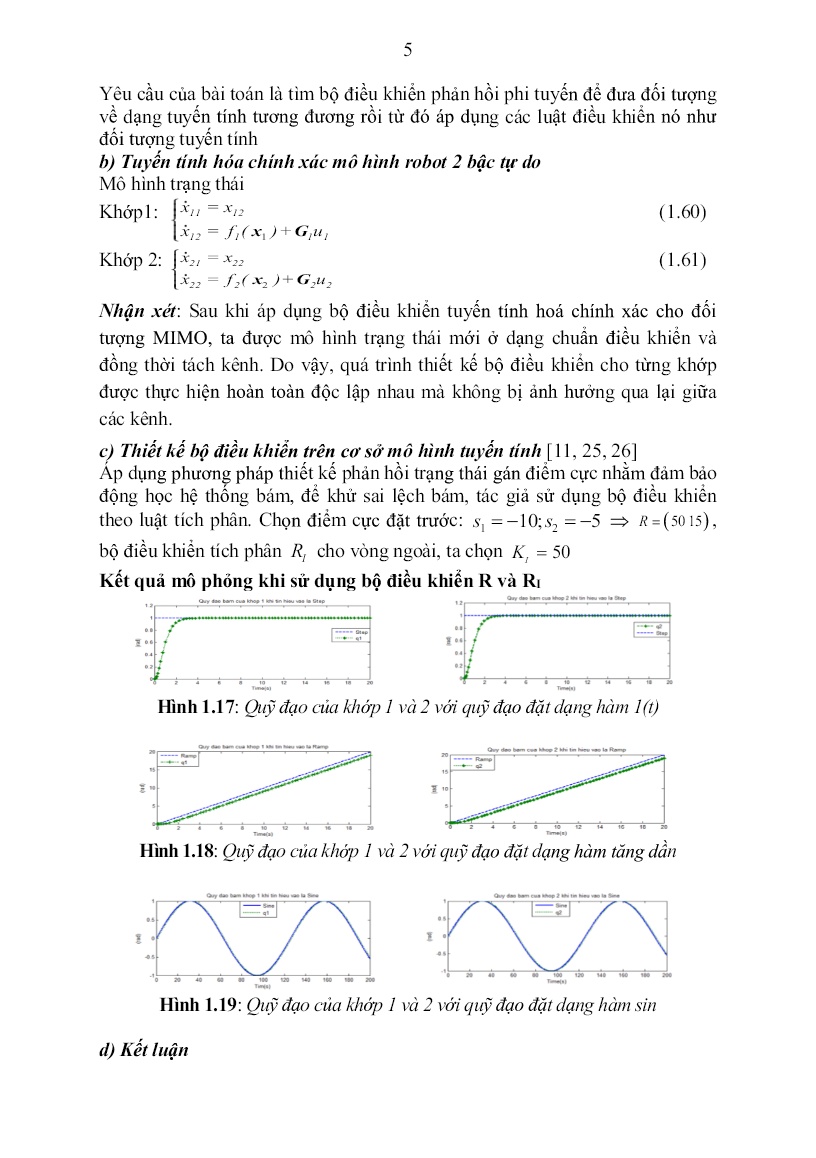
Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Luận án Thuật toán điều khiển thích nghi phi tuyến mới trên cơ sở mạng nơ ron nhân tạo cho robot công nghiệp", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Luận án Thuật toán điều khiển thích nghi phi tuyến mới trên cơ sở mạng nơ ron nhân tạo cho robot công nghiệp

ám quỹ đạo cho robot bằng phương pháp Jacobian xấp xỉ thích nghi a) Mô hình toán học của robot Phương trình động lực học tổng quát của robot n bậc tự do [30, 32]: 1 Hqq Hq NqqqGq , (1.73) 2 Tn nn trong đó: q [ q12 , q ,..., qn ] R là các biến khớp; Hq()R là ma trận quán tính, Rn là mô men đặt lên trục các khớp của robot, G() q Rn là thành phần trọng lực của robot, N(,) q q Rnn là ma trận đối xứng lệch. b) Thiết kế bộ điều khiển Luật điều khiển thích nghi trên cơ sở ma trận Jacobian xấp xỉ [35, 61]: ˆˆTTˆˆˆ ˆ J q,, T KD X KP X J q T KSx W q, q, q r, q r p (1.88) Trong đó: XXX d , XXX d ; KKKdp,, là các ma trận đường chéo cấp n xác định dương. Các thông số động học ước lượng Tˆ của mà trận Jacobian Jˆ q,Tˆ được cập nhật bởi luật sau: ˆ T Tq RY q, Kdp X K X (1.89) và các thông số động lực học pˆ được ước lượng bởi luật cập nhật sau: T pˆ W q, q, qrr,q S (1.90) trong đó: R R ff , Rnn là các ma trận đường chéo có các phần tử dương. c) Kiểm chứng thuật toán trên robot phẳng 3 thanh nối Các thông số thực của robot như sau: 2 ll12l3 ml11 m1,,,,,,, m 2 m 3 l 1 l 2 l 3lg 1 lg23, lg ; III 2 2 2 1 2 3 12 Quỹ đạo chuyển động mong muốn: 7 7 2 2 3 8 2 3 xd cos t t cos t t 18 25 375 18 150 1125 (1.106) 7 2 2 3 8 2 3 yd sin t t sin t t 1 18 25 375 18 150 1125 d 2 Kết quả mô phỏng: như hình 1.21 đến hình 1.22. Trường hợp 1: m1 6 kgm ; 2 4 kgm ; 3 2 kgl ; 1 0.7 ml ; 2 0.6 ml ; 3 0.5 m Hình 1.21: Quỹ đạo x và y trong không gian làm việc (trường hợp 1) Trường hợp 2: m1 10 kgm ; 2 8 kgm ; 3 6 kgl ; 1 0.8 ml ; 2 0.7 ml ; 3 0.6 m Hình 1.22: Quỹ đạo x và y trong không gian làm việc (trường hợp 2) d) Nhận xét: Từ các phân tích lý thuyết theo tiêu chuẩn ổn định Lyapunov cho thấy bộ điều khiển thích nghi sử dụng ma trận Jacobian xấp xỉ đảm bảo hệ thống ổn định toàn cục. Kết quả mô phỏng đã kiểm định hệ thống điều khiển là ổn định, các tín hiệu vị trí thực của tay máy robot hội tụ về các tín hiệu vị trí đặt với tốc độ hội tụ nhanh và sai số bám nhỏ ngay cả khi các thông số hệ thống là bất định kiểu hằng số. 1.2.2.4 Điều khiển thích nghi bền vững sử dụng kỹ thuật backstepping trong điều khiển chuyển động của robot Phương pháp thiết kế bộ điều khiển bền vững kết hợp kỹ thuật backstepping trong chuyển động bám quỹ đạo của robot khi có nhiễu tác động đảm bảo sự ổn định của hệ kín theo tiêu chuẩn ổn định Lyapunov. Phương pháp này có thể sử dụng để thiết kế bộ điều khiển cho robot có số bậc tự do lớn, có mô hình xác định và có nhiễu tác động [20, 21, 22]. 1.2.2.5 Điều khiển thích nghi robot trên cơ sở mờ và mạng nơ ron Sử dụng mạng Nơ ron (NN) để thiết kế điều cho điều khiển robot đảm bảo sai lệch bám và các sai lệch ước lượng trọng số là bị chặn, mang đến đặc tính bền vững cho bộ điều khiển kể cả khi đối tượng có tính phi tuyến, chưa biết đầy đủ thông tin về mô hình động lực học và cũng như khi có nhiễu tác 8 động. Ý nghĩa trong một số ứng dụng của NN điều khiển robot là phù hợp do chính động lực học của robot [24]. 1.3 Hướng nghiên cứu của luận án 1.3.1 Phát biểu bài toán Đối tượng robot n bậc tự do: Như đã trình bày ở phần 1.1, việc xác định chính xác mô hình của robot công nghiệp gặp nhiều khó khăn, đó là sự phức tạp trong việc xác định khối lượng, mô men cũng như kích thước hình học của robot, ngoài ra các tham số còn có thể bị thay đổi phụ thuộc vào chế độ công tác của robot... Do đó, mô hình động lực học tổng quát nhất của robot là mô hình trạng thái bất định kiểu hàm số. Đây cũng là mô hình của đối tượng trong bài toán điều khiển được đề cập đến trong luận án. Mục tiêu điều khiển: là xây dựng bộ điều khiển bám quỹ đạo đặt trước cho robot có mô hình bất định kiểu hàm số đảm bảo hệ kín ổn định bền vững toàn cục (GAS), sai lệch bám tiến về không và không chịu ảnh hưởng của nhiễu. 1.3.2 Phương pháp luận Căn cứ vào việc phân tích đặc tính động học của mô hình trạng thái robot, trên cơ sở nghiên cứu các phương pháp điều khiển phi tuyến, thích nghi và mạng nơ ron nhân tạo để từ đó đề xuất các giải thuật điều khiển đạt được mục tiêu điều khiển. Do vậy, định hướng nghiên cứu của luận án là đề xuất bộ điều khiển thích nghi bền vững mới trên cơ sở kết hợp điều khiển phi tuyến với mạng nơ ron nhân tạo. 1.4 Kết luận Chương 1 của luận án trình bày về phương pháp xây dựng mô hình động lực học của robot, phân tích các đặc tính đặc trưng của mô hình robot. Nghiên cứu một số phương pháp tổng hợp bộ điều khiển đặc trưng cho robot công nghiệp, mô phỏng và từ đó đánh giá khả năng phát triển thuật toán điều khiển mới trên cơ sở các phương pháp điều khiển này. Tuy nhiên, phần lớn các phương pháp nghiên cứu đến thời điểm hiện nay mới chỉ giải quyết được triệt để bài toán tổng hợp bộ điều khiển cho robot có mô hình xác định hoặc mô hình bất định kiểu hằng số, còn rất ít các đề xuất tổng hợp bộ điều khiển cho robot có mô hình bất định kiểu hàm số. Chương 2: ĐIỀU KHIỂN THÍCH NGHI TAY MÁY ROBOT SỬ DỤNG MẠNG NƠ RON TRÊN CƠ SỞ KỸ THUẬT BACKSTEPPING 2.1 Tổng hợp bộ điều khiển thích nghi sử dụng mạng nơ ron Xét đối tượng phi tuyến có cấu trúc truyền ngược [21, 22]: xi f i x1, x 2,,,,, x i g i x 1 x 2 x i x i 1 xn f n x g n x u (2.1) yx 1 T TTn ( n 1) n xx xxxRuR1, 2 ,...,n ; ; d xxx d 1 , d 2 ,..., dn yyy d , d ,..., d R ; y R; i 1,2,..., n 1 tương ứng là biến trạng thái, tín hiệu điều khiển, tín hiệu 9 đặt và đầu ra hệ thống. Trong đó fi (.) , fn (.) và gi (.) , gn (.) là những hàm số trơn bị chặn và bất định. 2.1.1 Xấp xỉ hàm số bằng mạng nơ ron nhân tạo Dựa vào các phân tích trong tài liệu [23, 37, 38], chọn MNN 3 lớp truyền thẳng là sự lựa chọn hợp lý với các giả thiết sau: g x Giả thiết 1: Biết dấu của ii , tồn tại một hằng số gi0 0 và biết trước các i hàm trơn gxii , như vậy: gi x i g i x i g i0 , x i R Giả thiết 2: véc tơ trạng thái mong muốn xdi với in 1,2,..., 1 là liên tục và i biết trước. xdi di R với di là những tập compact biết trước. Giả thiết 3: Cho một hàm trơn hZ và một xấp xỉ MNN (1.1) luôn tồn tại ** ˆˆ các trọng số lý tưởng W ,V để với 0; Z z ; W,V là các trọng số ước lượng của W *và V * . Sai số ước lượng trọng số đuợc xác định như sau: WWW ˆˆ **; VVV (2.2) Sử dụng MNN để xấp xỉ hàm trơn bất định h Z : Rm R Ta có cấu trúc mạng: hˆ Z W TTSVZ (2.3) (1.1) T với véc tơ đầu vào là: Z Z T ,1 (2.4) T ma trận trọng số từ lớp 2 đến lớp ra là W ( w12 , w ,..., w ) R (2.7) T m 1 ma trận trọng số từ lớp vào đến lớp 2 là V v12, v ,..., v R (2.8) Số lượng nơ ron trong một lớp luôn thỏa mãn 1. Sai số ước lượng MNN (2.3) có thể biểu diễn như sau: ˆTTTTTTTT ˆ**''ˆ ˆ ˆ ˆ ˆ WSVZSVZSSVZSVZ()()() W W W du (2.12) 2.1.2 Tổng hợp bộ điều khiển thích nghi trên cơ sở kỹ thuật backstepping Bước 1: [21, 22, 37] Xét (2.1), với i 1 ta có: x1 f 1()() x 1 g 1 x 1 x 2 (2.27) ˆˆTT Xấp xỉ hàm bằng mạng nơ ron: h1()() Z 1 W 1SVZ 1 1 1 (2.37) ta có tín hiệu điều khiển: 1 ˆˆTT 1 u 1 [ k 1 ( t ) z 1 W 1SVZ 1 ( 1 1 )] (2.38) g11()x 1 22 1 ˆˆTTˆˆ'' k1( t ) 1 g 1 ( z 1 yd ) d Z 1 W 1 S 1 S 1 V 1 Z 1 (2.39) F 1 0 Hằng số 1 0, trọng số NN cập nhật bởi ˆˆˆ' ˆT ˆ W1 ww 1[(SSVZ 1 1 1 1 ) z 1 1 W 1 ] (2.40) ˆ ˆT ˆ ' ˆ VZS1 vv 1[] 1W 1 1 z 1 1 W 1 10 thực hiện tương tự cho các in 2,..., 1 Bước n: Xét zxn n n 1 (2.93) chúng ta có: zn x n n 11 f n()() x g n x u n (2.94) Bộ điều khiển được chọn như sau: 1 u g()()() x z k t z WˆˆTT S V Z (2.102) NN nnn 1 1 1 nnnnnn gn ()x 1 22 1 ˆˆTTˆˆ'' ở đây: kn( t ) 1 g nnnn ( x 11 , z ) d Z nnn W S S nnn V Z (2.103) F n 0 với hằng số n 0 và luật học của mạng nơron Wˆ ()SSVZˆˆ ' ˆT z W ˆ n wn n nnnn wnn (2.104) VZSVˆ Wz ˆT ˆ ' ˆ n vn n n n n vn n 2.1.3 Phân tích tính ổn định Ta thấy sau mỗi bước xuất hiện một hàm xác định dương: z i (2.108) Vzi i(x i 11 , i ) d , i 2,3,..., n 0 và ta chọn nó làm hàm Lyapunov, đây là điểm mấu chốt quan trọng của phương pháp. Theo giả thuyết 1, chúng ta biết rằng: 1 i (x i 1 , i 1 ) g 1 ( x i 1 , i 1 ) / g i 0 (2.109) và các tính chất sau: 112 22zi (i) Vzi z i i(,)x i 11 z i i d z i d (2.110) 002 112 (ii) 2 zi (2.111) Vziiiiii z(,)(,)x 1 z 1 d g iiii x 1 z 1 d 00gi0 Ổn định và hiệu quả điều khiển của hệ thống kín được đề cập trong định lý 2.2 2.1.4 Tổng hợp ANNC cho robot 1 bậc tự do 2.1.4.1 Biến đổi mô hình về dạng truyền ngược chặt Xét mô hình tay máy 1 bậc tự do có phương trình như sau: 2 (I mlqKq ) Nc ( mlMlg ) .cos q u (2.133) T T Đặt: y x1;;,, x 1 x 2 x x 1 x 2 xx12 lúc này (2.133) viết lại: (2.134) x2 f(x ) G ( x ). u K x ml Ml gcos x 1 với f();() x Nc21 G x I ml22 I ml là các hàm bất định và được xấp xỉ bởi mạng nơ ron 3 lớp. 2.1.4.2 Tổng hợp ANNC Từ cơ sở phân tích ở phần 2.1.2, a có bộ điều khiển: 11 ˆˆTT TT 1 k 1()() t z 1 W 1 S 1 V 1Z 1 ; u z1 k 2()() t z 2 W 2 S 2 V 2Z 2 (2.135) 2.1.4.3 Kết quả mô phỏng Các thông số bộ điều khiển được chọn: 3.0; 1.0; 5.0 ; 1 10 2 ; 1 10 43 ; 1 10 12 ww12 v12v diag 1.0 ; diag 10.0 ww12 vv12 ˆ ˆ ˆ ˆ và các trọng số khởi tạo: W1(0) 0.0, W2 (0) 0.0 ; V1 (0) ,V2 (0) lấy ngẫu nhiên Các thông số động học của tay máy 1 DOF như bảng 2.1: 22 Th1: B 0.2( kgmsI / ); 0.05( kgmM . ); 1( kgm ); 0.1( kgl ); 0.4( ml );c 0.15( m ) 22 Th2: B 0.2( kgmsI / ); 0.05( kgmM . ); 1.5( kgm ); 0.5( kgl ); 0.6( ml );c 0.3( m ) Cấu trúc NN được chọn với số nơ ron ở lớp vào và lớp ẩn là 3,3 biểu diễn trong hình 2.4a và 6,6 biểu diễn trong hình 2.4b, với tham số động học của robot được mô phỏng như nhau (trường hợp 1 trong bảng 2.1). a) 3 nơ ron b) 6 nơ ron Hình 2.4: Quỹ đạo và sai lệch quỹ đạo khi số nơ ron lớp vào và lớp ẩn thay đổi Kết quả mô phỏng hình 2.4 cho thấy: khi chọn NN có số phần tử nơ ron lớn hơn trong một lớp thì chất lượng của hệ thống cũng tốt hơn. Nhưng trong thực tế, chúng ta cũng không thể chọn số nơ ron trong một lớp quá lớn vì nó sẽ ảnh hưởng đến thời gian huấn luyện mạng đẫn đến khó đảm bảo được tính thời gian thực của bộ điều khiển. Dựa vào kết quả trên, NN thích hợp xấp xỉ hàm phi tuyến là mạng nơ ron có lớp vào và lớp ẩn với 6 nơ ron. Để kiểm tra ảnh hưởng của sự thay đổi tham số robot, luận án sử dụng NN trong đó lớp ẩn và lớp vào với 6 nơ ron và tham số của robot thay đổi theo các giá trị được biểu diễn trong bảng 2.1. Các kết quả mô phỏng được biểu diễn ở hình 2.5. a) Trường hợp 1 b) Trường hợp 2 Hình 2.5: Quỹ đạo và sai lệch quỹ đạo khi thay đổi thông số động học của robot 12 Nhận xét: Qua các kết quả mô phỏng cho thấy - Khi tăng số nơ ron trong các lớp thì thời gian đáp ứng quá độ sẽ giảm (Hình 2.4 a và b). - Khi thay đổi các thông số của mô hình robot (m và l) chất lượng của hệ thống kín không bị thay đổi (Hình 2.5 a và b) khi chọn NN có cấu trúc phù hợp. - ANNC có khả năng ứng dụng cho Robot n bậc tự do. 2.2 Tổng hợp bộ ANNC cho robot n bậc tự do 2.2.1 Biến đổi mô hình về dạng truyền ngược chặt Xét mô hình động lực học của robot n bậc tự do như (1.8) Hqq()(,)()() Cqqq Gq Fqdd (2.139) Qua một số phép biến đổi và dựa trên đặc tính đối xứng xác định dương của ma trận H ta có thể chuyển mô hình (2.1.39) về dạng n hệ con truyền ngược chặt như sau: qxii 1 xi1 qxii 2 , với xi ;in 1,2,..., . (2.144) xi2 qi x i2 f i()x i u i Trong đó: fii()x là các hàm trơn chưa biết và bị chặn. 2.2.2 Tổng hợp ANNC Từ (2.144) ta có bộ điều khiển cho mỗi hệ con của robot n bậc tự do: 1 u g( x ) z k ( t ) z WˆˆTT S ( V Z ) ; i 1,2,..., n . (2.145) i i1 i 1 i 1 i 2 i 2 i 2 i 2 i 2 i 2 gxii22() Luật cập nhật tham số: Wˆ (SSVZVZSVˆ ˆ'' ˆTT ) z W ˆ ; ˆ ( W ˆ ˆ z ˆ ; i 1,2,..., n . (2.146) iwi i iiii wii i vi iiii vii Phép đổi biến 1 (2.147) ui H( q i ) i i H ( q i ) u i ; i 1,2,..., n . 2.2.3 Tổng hợp ANNC cho robot 2 bậc tự do 2.2.3.1 Biến đổi mô hình về dạng truyền ngược chặt Tương tự như mục 2.2.1, nhưng với i 1,2. 2.2.3.2 Tổng hợp ANNC Tương tự như mục 2.2.2, nhưng với 2.2.3.3 Kết quả mô phỏng Các tham số NN chọn như phần trên, thông số động học của tay máy thay đổi theo các giá trị biểu diễn ở bảng 2.2. Th1: m1 5 kg ; m 2 3 kg ; l 1 0.45 m ; l 2 0.35 m Th1: m1 7 kg ; m 2 5 kg ; l 1 0.65 m ; l 2 0.55 m Quỹ đạo đặt: qt1d sin( ) và q2d 0.5sin(t) +sin(0.5t) , tham số động học của hệ thống thay đổi theo bảng 2.2 và thành phần bất định được xấp xỉ bằng NN có 6 nơ ron ở lớp vào và lớp ẩn, ta được các kết quả mô phỏng biểu diễn từ hình 2.8 đến hình 2.11. 13 a) Trường hợp 1 b) Trường hợp 2 Hình 2.8: Quỹ đạo và sai lệch quỹ đạo của khớp 1 a) Trường hợp 1 b) Trường hợp 2 Hình 2.9: Quỹ đạo và sai lệch quỹ đạo của khớp 2 a) Trường hợp 1 b) Trường hợp 2 Hình 2.10: Vận tốc và sai lệch vận tốc của khớp 1 a) Trường hợp 1 b) Trường hợp 2 Hình 2.11: Vận tốc và sai lệch vận tốc của khớp 2 Nhận xét: Các kết quả mô phỏng cho thấy ANNC đáp ứng được đầy đủ các yêu cầu đặt ra đối với bài toán điều khiển bám cho robot n bậc tự do mô hình bất định dạng hàm số. Điều này cho thấy khả năng ứng dụng ANNC cho các đối tượng robot công nghiệp trong thực tế. 14 2.4 Kết luận chương 2 Chương 2 trình bày phương pháp luận về thiết kế bộ điều khiển cho đối tượng phi tuyến bất định hàm số dạng truyền ngược chặt bằng cách kết hợp kỹ thuật backstepping với mạng nơ ron nhân tạo, đề xuất phương pháp chuyển đổi mô hình động lực học của robot về dạng thích hợp với ANNC. Thay đổi cấu trúc của NN để xác định được cấu trúc phù hợp đảm bảo khi tham số động học của robot thay đổi chất lượng hệ thống điều khiển tự động không đổi. Các kết quả mô phỏng kiểm chứng cho mô hình robot 2 bậc tự do cho thấy tính đúng đắn của giải thuật điều khiển và khả năng ứng dụng trong thực tế cho robot công nghiệp Do giải thuật ANNC chưa quan tâm đến việc khắc phục nhiễu từ bên ngoài tác động vào đối tượng điều khiển nên không đảm bảo được chất lượng hoạt động của robot trong trường hợp có nhiễu. Mặt khác để áp dụng phương pháp backstepping này yêu cầu bài toán phải tuân thủ điều kiện của giả thiết 1. Có nghĩa là phải tìm được giá trị chặn trên gxii() của của hàm gii()x , mà trong thực tế có thể có những trường hợp khó khăn hoặc không thể tìm được vì vậy không thể áp dụng được phương pháp này và đây cũng là hạn chế chính của phương pháp. Để khắc phục hạn chế trên các nghiên cứu tiếp theo nhằm giải quyết đồng thời tính bất định kiểu hàm số của robot và khắc phục nhiễu. Luận án đề xuất phương pháp thiết kế bộ điều khiển trượt nơ ron thích nghi bền vững (RANNSMC) cho tay máy robot n bậc tự do. Chương 3 ĐIỀU KHIỂN TRƯỢT NƠ RON THÍCH NGHI BỀN VỮNG CHO TAY MÁY ROBOT BẤT ĐỊNH HÀM SỐ 3.1 Đặt bài toán tổng hợp bộ điều khiển trượt Xét đối tượng phi tuyến bất định hàm số bậc hai thụ động dạng truyền ngược, có điểm cân bằng tại gốc tọa độ có mô hình được thể hiện như sau [10], [27]: xx 12 x ; với x = 1 (3.1) x2 f()x u d x 2 yx 1 trong đó f x là hàm phi tuyến trơn, bất định bị chặn và hệ (3.1) có điểm cân bằng tại gốc tọa độ. d là nhiễu ngoại tác động lên hệ thống. 3.2 Tổng hợp bộ điều khiển trượt Định nghĩa mặt trượt: S() e e e (3.2) trong đó: e w x1; e w x 1 w x 2 . Để đảm bảo khi limet ( ) 0 , phải t chọn hệ số 0 và mặt trượt đảm bảo điều kiện S(0) 0 . 1 Chọn hàm Lyapunov cho hệ kín như sau: VSS() 2 (3.3) SMC 2 15 Đạo hàm theo thời gian hàm V . và để ý đến điều kiện trượt trong biến đổi, cuối cùng ta xác định được tín hiệu điều khiển trượt uSMC : uSMC Ksgn( S ) w w x1 f (x ) (3.8) Muốn tổng hợp được bộ điều khiển trượt (3.8) thì cần phải biết trước hàm f ()x . Nhưng thực tế đối tượng có f ()x là bất định. Do vậy, luận án đề xuất sử dụng mạng nơ ron để xấp xỉ hàm f ()x . Thay ff(.) ˆ (.) vào (3.8) ta được bộ điều khiển trượt cho đối tượng bất định hàm. ˆ uSMC Ksgn( S c ) w w x1 f (x ) (3.9) 3.3 Xấp xỉ hàm bất định bằng mạng nơ ron hướng tâm Từ (3.1) bỏ qua tác động của nhiễu, biến đổi ta có thể viết lại dưới dạng sau: x()()()t A x t Bu t F x (3.10) yx 1 T 01 0 T trong đó, x()()();t x12 t x t AB ; ; FF xx 0 aa21 22 1 với F xx a21 x 1 a 22 x 2 f ; aa21 0; 22 0 (3.12) Cấu trúc mạng RBFNN được mô tả như hình 3.3. Hình 3.3: Cấu trúc mạng RBFNN khi đó: FW xx ii (3.14) i 1 Trong đó các hàm cơ sở i x được chọn dưới dạng [23] tr59: xx CC22 x exp ii exp (3.15) i bb22 ii i 1 Với Ci là véc tơ 2 chiều biểu diễn tâm của hàm cơ sở thứ i , bi biểu diễn độ trải rộng của hàm cơ sở. Động học của mô hình xấp xỉ được miêu tả bằng phương trình: xˆˆ()()()t A x t B u t Fˆ x m m m m (3.20) yCˆ m xˆ trong đó: xm ()t - véc tơ trạng thái; ABmm, - các ma trận với kích thước tương T ứng AABBFF ; ;ˆ xx 0 ˆ ; C 10T . Lấy phương trình mm m 16 (3.11) trừ cho phương trình (3.20) ta được: E()(), t Am E t F x (3.21) T trong đó, FFFFx xˆ x 0 x ; (3.22) E( t ) xx ( t )m ( t ); FFF x x ˆ x . Quá trình hiệu chỉnh được thực hiện trên cơ sở sử dụng véc tơ sai lệch Et() và đảm bảo để Et( ) 0, nghĩa là đảm bảo để hệ thống (3.21) ổn định. Định lý sau đây xác định điều kiện đủ để hệ thống (3.1) ổn định tiệm cận. 3.4 Phân tích tính ổn định của hệ thống Định lý 3.1: Đối tượng (3.1) điều khiển RANNSMC (3.9) với bộ xấp xỉ RBFNN (3.16) có luật cập nhật véc tơ trọng số W (x )( p12 e 1 p 22 e 2 ) ổn định tiệm cận. Chứng minh Chọn hàm Lyapunov cho hệ (3.21) như sau: V(,) E W ETT PE W W (3.23) với P là ma trận đối xứng xác định dương Đạo hàm V (.) theo thời gian ta được: VEW(,) EPETTTT EPE WW WW (3.24) Biết đổi và thay véc tơ trọng số vào, cuối cùng ta có được: TTT VEW( , ) E ( APmm PAE ) EQE 0 (3.30) Vậy hàm V . định nghĩa ở (3.23) chính là hàm Lyapunov của hệ, như vậy định lý đã được chứng minh □. 3.5 Tổng hợp RANNSMC cho robot n bậc tự do 3.5.1 Biến đổi mô hình về dạng truyền ngược chặt Các bước biến đổi như mục 2.2.1, với mô hình robot biểu diễn ở dạng truyền ngược cho phép sử dụng phương pháp thiết kế bộ điều khiển trượt thích nghi bền vững (RANNSMC) có cấu trúc như hình 3.6. 3.5.2 Tổng hợp bộ điều khiển Cấu trúc bộ điều khiển Hình 3.6: Hệ thống điều khiển robot n DOF sử dụng bộ điều khiển RANNSMC - Tổng hợp bộ điều khiển trượt: xét mô hình (3.31) với fi (.) biết trước. Các bước Tổng hợp như phần 3.2, ta có bộ điều khiển cho các khớp: 17 uKSi sgn( i ) qq id id qfqqi i i ( i , i ); 1,2,..., n . (3.34) Nhưng thực tế thì fiii(,) q q trong (3.31) là hàm phi tuyến bất định. Do vậy, để sử dụng được bộ điều khiển (3.34), luận án đề xuất sử dụng cấu trúc RBFNN để xấp xỉ hàm fiii(,) q q . - Xấp xỉ hàm phi tuyến bất định Nhờ mạng nơ ron xấp xỉ ta có được F q, q từ đó dễ dàng xác định f q, q theo biểu thức sau: f q,,() q F q q a21 q a 22 q (3.35) trong đó aa21 0; 22 0 là các tham số được chọn trước, lúc này ta có: ˆ uKSi sgn( i ) qq id id qfqqi i i ( i , i ); 1,2,..., n . (3.36) Luật cập nhật trọng số của mạng: Wii (,) q q p21 e 1 p 22 e 2 (3.29) Quá trình hiệu chỉnh được thực hiện trên cơ sở sử dụng véc tơ sai lệch Et() và đảm bảo để Et( ) 0 . 3.6. Tổng hợp RANNSMC cho robot 3 bậc tự do 3.6.1 Biến đổi mô hình về dạng truyền ngược chặt Xét robot Scara 3 bậc tự do bao gồm có hai khớp quay và một khớp tịnh tiến, Các khâu 1, 2 và 3 có khối lượng và chiều dài lần lượt là: m1,;,;,. l 1 m 2 l 2 m 3 l 3 3.6.2 Tổng hợp RANNSMC Các bước thiết kế được thực hiện như ở mục 3.5.2, ta có: uj Ksgn( S j ) q jd q jd q j f j với jn 1,2,..., (3.64) 3.6.3 Kết quả mô phỏng Các thông số của robot cho như sau: m1 3.27 kgm ; 2 2.93 kgm ; 3 2.13 kgl ; 1 0.45 ml ; 2 0.45 ml ; 3 0.565 Các thông số bộ điều khiển: 10;K 300 Quỹ đạo đặt cho 3 khớ
File đính kèm:
 luan_an_thuat_toan_dieu_khien_thich_nghi_phi_tuyen_moi_tren.pdf
luan_an_thuat_toan_dieu_khien_thich_nghi_phi_tuyen_moi_tren.pdf

