Tóm tắt Luận án Bài toán chẩn đoán kỹ thuật công trình trong trường hợp thiếu số liệu và ứng dụng cho dầm bê tông cốt thép bị ăn mòn

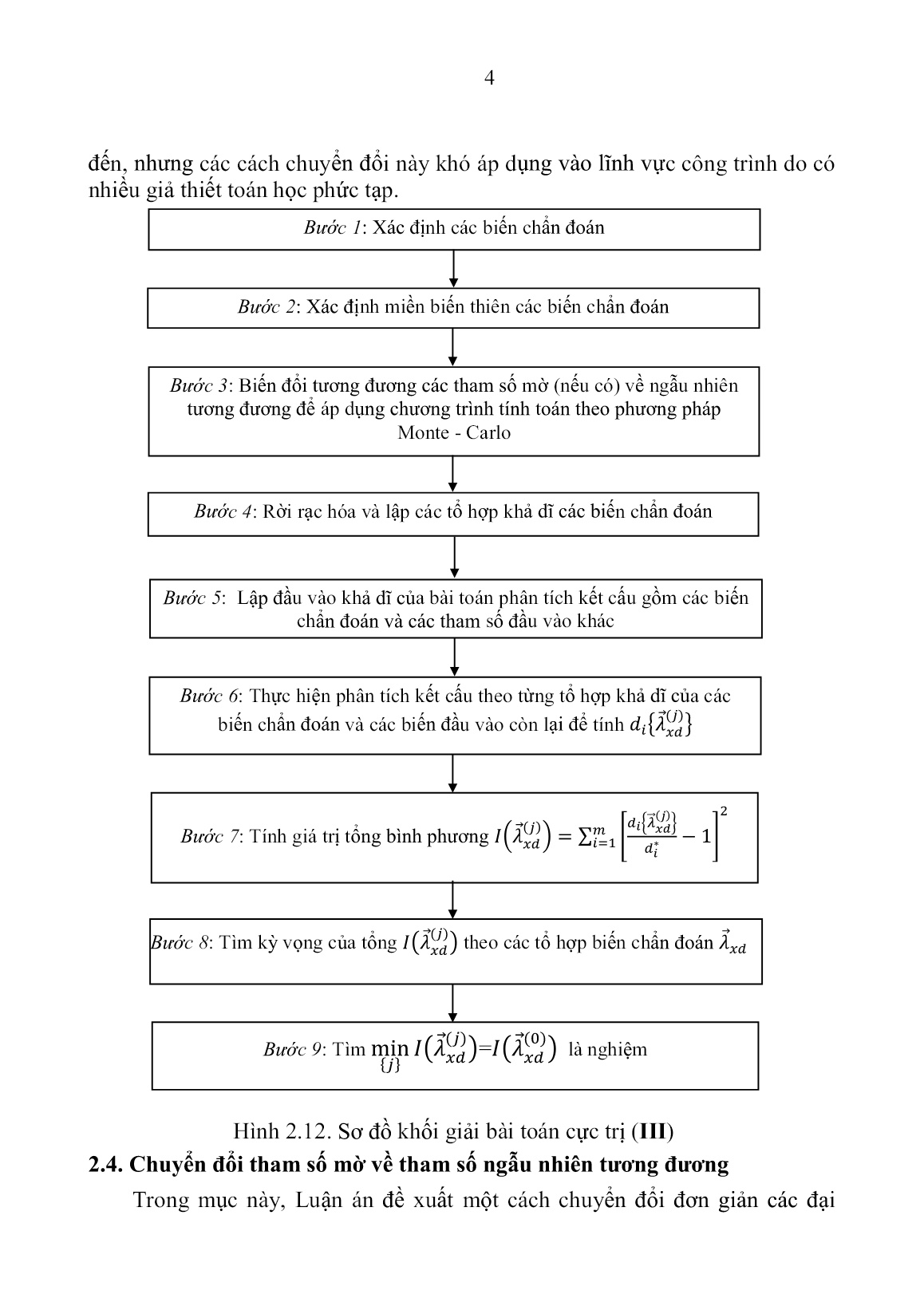
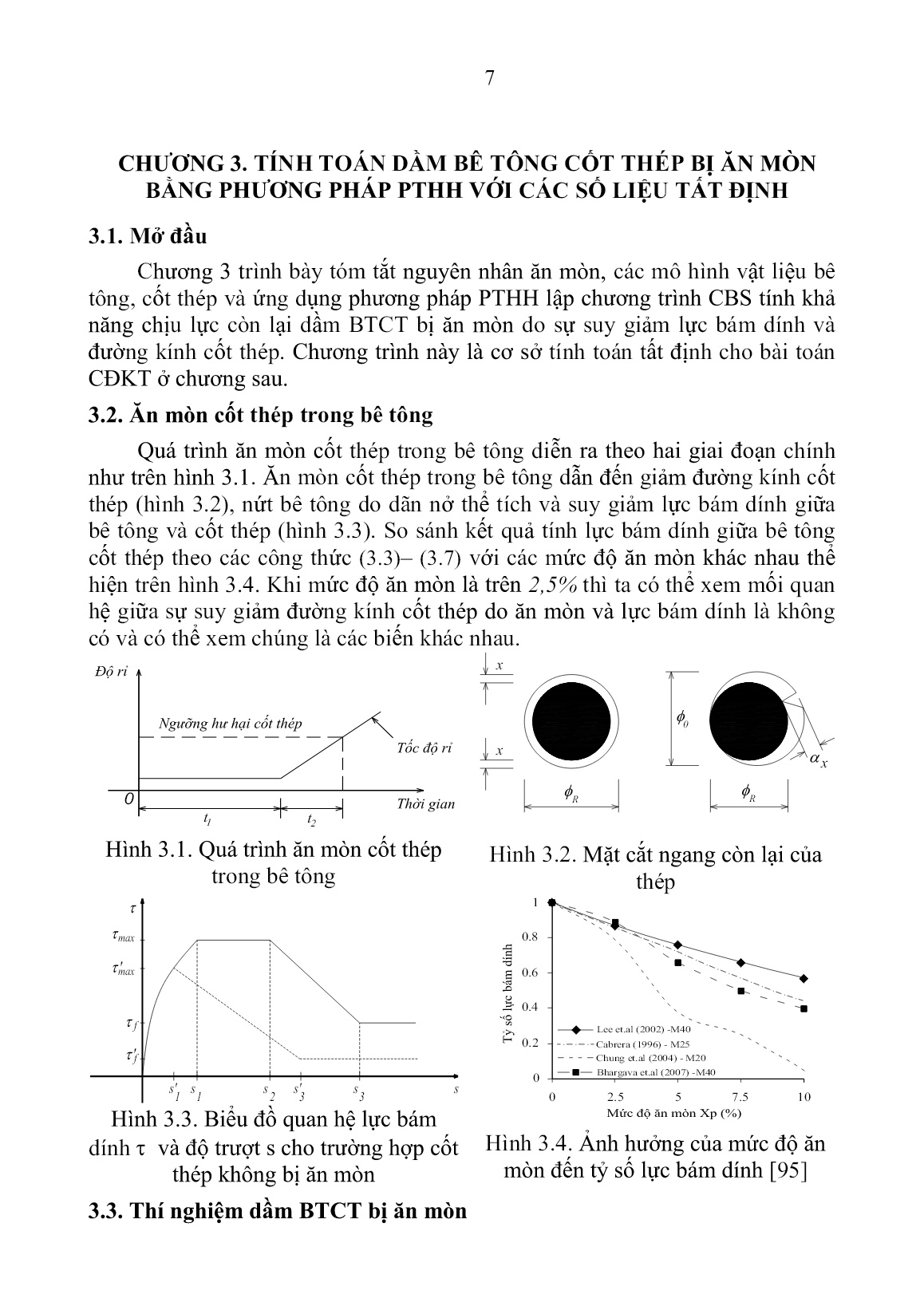
ng sai của đại lượng mờ. 
2.5. Phương pháp giải bài toán CĐKT công trình khi thiếu số liệu 
Sơ đồ khối để giải bài toán CĐKT công trình trong trường hợp thiếu số 
liệu, cụ thể là bài toán cực trị (III), thể hiện trên hình 2.12. Do rời rạc hóa miền 
các biến chẩn đoán D nên sẽ có sai số. Theo khả năng tính toán và yêu cầu về 
độ chính xác của lời giải, sau khi thực hiện tính toán theo 9 bước của sơ đồ 
khối, ta coi đó là “nghiệm thô”. Để tăng độ chính xác, ta tiến hành bao nghiệm 
thô bởi một miền 'D D (D’ bé hơn D) và thực hiện tương tự theo sơ đồ khối 
trên với bước lưới nhỏ hơn. 
2.6. Đánh giá về sai số và tính đa trị của nghiệm bài toán chẩn đoán 
Nhằm khắc phục tính vô nghiệm của bài toán CĐKT, thay vì chọn tiêu 
chuẩn đồng nhất hóa giữa số liệu đo đạc và số liệu lý thuyết, luận án đã chọn 
tiêu chuẩn độ lệch bình phương bé nhất vì các lý do sau: 
- Tiêu chuẩn đồng nhất hóa giữa số liệu đo đạc và số liệu lý thuyết dẫn 
đến giải hệ phương trình đại số siêu việt, phức tạp. Các phương trình có thể vô 
nghiệm, đặc biệt trường hợp sai số đo đạc là lớn; 
- Tiêu chuẩn độ lệch bình phương bé nhất dẫn đến bài toán cực trị. Do đó, 
ta luôn chọn được nghiệm làm cho tổng bình phương sai lệch giữa số liệu thực 
nghiệm và số liệu mô hình là bé nhất, nghĩa là chọn được mô hình lý thuyết gần 
nhất với số liệu thực nghiệm. Tất nhiên, để giá trị bé nhất (2.24) càng gần với 
giá trị lý tưởng thì ta phải xem xét lại 2 yếu tố: Mô hình toán học đã sát với 
thực tế chưa? và số liệu đo đạc đã đủ tin cậy chưa?. Nếu 2 yếu tố này đã thỏa 
mãn thì bài toán cực trị bao giờ cũng có lời giải vì cụ thể đối tượng đang tồn tại. 
Ta nhận thấy rằng, nghiệm chẩn đoán theo sơ đồ 9 bước như trên hình 
2.12 có thể đa trị, nghĩa là, có nhiều giá trị khác nhau của 𝐼 (𝜆𝑥𝑑
(𝑗)) cùng đạt min. 
Điều này được khẳng định ngay bằng toán học vì số lượng ẩn rất lớn, trong khi 
số phương trình (rút ta từ các số liệu đo đạc) lại rất hạn chế. Vì vậy để tiến tới 
lời giải có ý nghĩa thực tế thì cần phải có những chỉ tiêu nào đó để chọn 
nghiệm. Có 2 cách để khắc phục khó khăn trên là: Bổ sung thông tin bằng cách 
6 
khảo sát thêm, tất nhiên càng nhiều số liệu đo đạc tin cậy thì ta có thể chọn 
nghiệm tin cậy hơn và căn cứ vào các kiến thức, tài liệu thiết kế và kinh nghiệm 
của các nhà kỹ thuật để chọn nghiệm hợp lý. 
2.7. Kiểm tra độ tin cậy của thuật toán đề xuất 
So sánh kết quả chẩn đoán chiều dài của một dầm công xôn chịu tải trọng 
ngang theo kết quả đo dao động tại một số điểm trên dầm bằng phương pháp đề 
xuất với kết quả chẩn đoán đã được các tác giả Nguyễn Cao Mệnh và Trần 
Trọng Toàn giải quyết, cho thấy kết quả chẩn đoán là tin cậy được. 
2.8. Thí dụ tính toán theo phương pháp đề xuất 
Đưa ra một ví dụ có 2 trường hợp để minh họa và làm rõ phương pháp 
giải bài toán chẩn đoán kỹ thuật công trình cho các trường hợp tham số là tất 
định, ngẫu nhiên và mờ. Các ví dụ đã cho thấy tính khả thi và độ tin cậy của 
phương pháp giải đề xuất. Từ đó, tác giả sẽ nghiên cứu bài toán chẩn đoán khả 
năng chịu lực còn lại của kết cấu bê tông cốt thép bị ăn mòn, đây là một bài 
toán đặt ra nhiều trong thực tế nhưng chưa được giải quyết trọn vẹn. 
2.9 Kết luận chương 2 
1. Phân loại và thành lập bài toán CĐKT trong trường hợp thiếu số liệu 
dựa vào tiêu chuẩn độ lệch bình phương bé nhất nhằm khắc phục tính vô 
nghiệm của bài toán CĐKT mà tiêu chuẩn đồng nhất hóa thường gặp. 
2. Đề xuất một sơ đồ khối gồm 9 bước để giải bài toán CĐKT trong 
trường hợp thiếu số liệu, có các tham số tất định, ngẫu nhiên và mờ cùng tham 
gia, đồng thời phương trình trạng thái chỉ có nghiệm số. Phương pháp này cho 
phép tận dụng các thuật toán và chương trình phân tích kết cấu tất định hiện có, 
đồng thời khắc phục được các hạn chế của các phương pháp phân tích và 
CĐKT công trình trong trường hợp thiếu số liệu hiện nay. 
3. Chuyển đổi tham số mờ về ngẫu nhiên tương đương để sử dụng phương 
pháp Monte – Carlo. Việc chuyển đổi được thực hiện đơn giản hơn so với các 
phương pháp toán học chính xác, có thể ứng dụng dễ dàng vào bài toán chẩn 
đoán kỹ thuật công trình. 
4. So sánh kết quả chẩn đoán chiều dài của dầm công xôn chịu tải trọng 
ngang của Nguyễn Cao Mệnh và Trần Trọng Toàn với phương pháp đề xuất 
cho thấy kết quả chẩn đoán là tin cậy, sai số bé chấp nhận được. 
5. Một thí dụ có 2 trường hợp để minh họa và làm rõ phương pháp giải bài 
toán CĐKT công trình. 
7 
CHƯƠNG 3. TÍNH TOÁN DẦM BÊ TÔNG CỐT THÉP BỊ ĂN MÒN 
BẰNG PHƯƠNG PHÁP PTHH VỚI CÁC SỐ LIỆU TẤT ĐỊNH 
3.1. Mở đầu 
Chương 3 trình bày tóm tắt nguyên nhân ăn mòn, các mô hình vật liệu bê 
tông, cốt thép và ứng dụng phương pháp PTHH lập chương trình CBS tính khả 
năng chịu lực còn lại dầm BTCT bị ăn mòn do sự suy giảm lực bám dính và 
đường kính cốt thép. Chương trình này là cơ sở tính toán tất định cho bài toán 
CĐKT ở chương sau. 
3.2. Ăn mòn cốt thép trong bê tông 
Quá trình ăn mòn cốt thép trong bê tông diễn ra theo hai giai đoạn chính 
như trên hình 3.1. Ăn mòn cốt thép trong bê tông dẫn đến giảm đường kính cốt 
thép (hình 3.2), nứt bê tông do dãn nở thể tích và suy giảm lực bám dính giữa 
bê tông và cốt thép (hình 3.3). So sánh kết quả tính lực bám dính giữa bê tông 
cốt thép theo các công thức (3.3)– (3.7) với các mức độ ăn mòn khác nhau thể 
hiện trên hình 3.4. Khi mức độ ăn mòn là trên 2,5% thì ta có thể xem mối quan 
hệ giữa sự suy giảm đường kính cốt thép do ăn mòn và lực bám dính là không 
có và có thể xem chúng là các biến khác nhau. 
Hình 3.1. Quá trình ăn mòn cốt thép 
trong bê tông 
Hình 3.2. Mặt cắt ngang còn lại của 
thép 
Hình 3.3. Biểu đồ quan hệ lực bám 
dính  và độ trượt s cho trường hợp cốt 
thép không bị ăn mòn 
Hình 3.4. Ảnh hưởng của mức độ ăn 
mòn đến tỷ số lực bám dính [95] 
3.3. Thí nghiệm dầm BTCT bị ăn mòn 
0
t2t1

R

R

0
 x
x
x

max '
max
f
f '
s
3
s
3
s'
2
s
1
s
1
s'
Lee et.al (2002) -M40
Cabrera (1996) - M25
Chung et.al (2004) - M20
Bhargava et.al (2007) -M40
0 2.5 5 7.5 10
0
0.2
0.4
0.6
0.8
1
8 
Rodriguez và cộng sự đã nghiên cứu rất chi tiết trong phòng thí nghiệm về 
ảnh hưởng của sự ăn mòn cốt thép đến khả năng chịu lực của dầm BTCT. Số 
lượng mẫu dầm BTCT nghiên cứu là 31 với các mức độ ăn mòn khác nhau 
(hình 3.5). Bản đồ chi tiết đường nứt bê tông được thiết lập cho từng dầm (hình 
3.6). Từ bản đồ này, Rodriguez và cộng sự đã đưa ra dự báo mức suy giảm lực 
bám dính giữa bê tông và cốt thép max. Bốn dạng phá hoại cũng như thứ tự phá 
hoại khác nhau đã được quan sát (hình 3.8). 
Hình 3.5. Cấu tạo dầm thí nghiệm bê tông cốt thép của Rodriguez 
Hình 3.6. Sơ đồ vết nứt do sự ăn mòn của dầm 
Luận án chỉ xét dạng phá hoại 1 của dầm BTCT do cốt thép bị ăn mòn. 
3.4. Mô hình vật liệu bê tông và cốt thép (hình 3.10 và 3.11) 
2300
1
1
2
0
0
150
1-1
1
2
3
1
2
3
1.5
2.0
1.0
0.3
1.2
0.3
0.5
1.4
0.2
0.3
0.7 1.0
0.3
1.5 1.0
1.3
0.2
2.4
0.7
1.2
0.4
0.2
0.6 34 1.2 1.5 0.8 0.9
1.5
0.8
2.0
0.2
0.8
2.0
0.4 0.3
1.7 1.0
0.3
0.7
0.8
1.0
0.6
0.3
0.2
0.5
0.7
Hình 3.8. Các dạng phá hoại quan sát được trên dầm 
800 400 800
2
0
0
1
2
4 3
PP
9 
Hình 3.10. Mô hình ứng suất biến dạng của bê tông khi nén (a), khi kéo (b) 
Hình 3.11. Mô hình ứng suất biến dạng của cốt thép 
3.5. Mô hình PTHH tính toán dầm bê tông cốt thép bị ăn mòn 
Khi giải bài toán CĐKT dầm BTCT bị ăn mòn, ta gặp một số khó khăn: 
- Các chương trình hiện nay về tính toán dầm BTCT có xét đến sự ăn 
mòn cốt thép như Ansys, Atena, Abaqus, Diana,... đòi hỏi phải chia dầm thành 
nhiều phần tử. Ví dụ: Ali Ghods phải chia 100 đến 300 phần tử theo mỗi trục 
[68], Yang Xiaoming cũng phải sử dụng hàng ngàn phần tử để phân tích [112]; 
- Việc tính toán dầm BTCT bị ăn mòn là bài toán phi tuyến vật lý, phải 
dùng phép giải lặp như Newton – Raphson, Newton – Raphson cải tiến,...; 
- Bản thân phương pháp giải bài toán CĐKT công trình trong trường hợp 
thiếu số liệu đề xuất ở chương 2 dẫn đến sử dụng phương pháp Monte – Carlo 
cũng là một phép giải rất nhiều lần. 
Do đó cần thiết phải lập một chương trình PTHH tính dầm BTCT bị ăn 
mòn nhỏ gọn, nhanh hơn và có thể kết hợp với thuật toán chẩn đoán dầm BTCT 
bị ăn mòn trong trường hợp thiếu số liệu đề xuất ở chương 2. 
Phần tử dầm BTCT có kể đến lực bám dính bao gồm ba phần tử ghép lại 
như hình 3.12: a) phần tử bê tông, b) phần tử cốt thép và c) phần tử tiếp xúc. 
Mỗi đầu phần tử dầm bê tông cốt thép có nhiều điểm nút: 
- Các điểm nút liên kết phần tử bê tông và phần tử tiếp xúc, điểm nút này 
có 3 bậc tự do gồm chuyển vị theo trục X, Y và góc xoay quanh trục Z; 


E
K
tu


fcc
Ec

su
fct
a) b)
fct K


fsy
su


fsy
Es
EST
a) b)
10 
- Các điểm nút liên kết phần tử tiếp xúc với phần tử cốt thép, mỗi điểm 
nút này có 1 bậc tự do là chuyển vị dọc trục X. 
Chuyển vị nút của phần tử dầm BTCT gồm chuyển vị dọc u, chuyển vị 
ngang w, góc xoay  và chuyển vị dọc của cốt thép 𝑢𝑠𝑖, trong đó số lượng ẩn 𝑢𝑠𝑖 
phụ thuộc vào số lượng thanh thép trong dầm. 
Hình 3.12. Phần tử dầm bê tông cốt thép 
Hình 3.14. Phần tử bê tông 
Hình 3.15. Phần tử cốt thép 
Hình 3.16. Phần tử tiếp xúc: a) Mặt cắt dọc; b) Mặt cắt ngang 
 Phần tử bê tông gồm chuyển vị dọc xấp xỉ theo 𝑢 = 𝑁𝑢1𝑢1+𝑁𝑢2𝑢2 với 
𝑁𝑢1 = 1 − 𝑥 𝐿;⁄ 𝑁𝑢2 = 𝑥 𝐿⁄ , chuyển vị ngang 𝑤 = 𝑁𝑤1𝑤1+𝑁𝑤2𝜃1+𝑁𝑤3𝑤2 +
𝑁𝑤4𝜃2 với 𝑁𝑤1, 𝑁𝑤2, 𝑁𝑤3 và 𝑁𝑤4là các hàm dạng Hermite (hình 3.14). 
Phần tử cốt thép chỉ có chuyển vị dọc theo trục X như hình 3.15. Sử dụng 
giả thiết tiết diện phẳng, tính được: 
𝑢𝑠 = 𝑁𝑠1𝑤1 + 𝑁𝑠2𝜃1 + 𝑁𝑠3𝑤2+𝑁𝑠4𝜃2 + 𝑁𝑠5𝑢𝑠1 + 𝑁𝑠6𝑢𝑠2 (3.22) 
trong đó 𝑁𝑠1, 𝑁𝑠2, 𝑁𝑠3, 𝑁𝑠4, 𝑁𝑠5, 𝑁𝑠6 là các hàm dạng của phần tử cốt thép: 
Y
XZ
1 2
y
1
3
2
4
y
1 2
43
t 1,2
3,4
11 
𝑁𝑠1 = −𝑦𝑖𝑁𝑤1
′ ; 𝑁𝑠2 = −𝑦𝑖(𝑁𝑤2
′ − NΔ1); 𝑁𝑠3 = −𝑦𝑖𝑁𝑤3
′ 
𝑁𝑠4 = −𝑦𝑖(𝑁𝑤4
′ − NΔ2); 𝑁𝑠5 = 1 −
𝑥
𝐿⁄ ; 𝑁𝑠6 =
𝑥
𝐿⁄ 
(3.23) 
Phần tử tiếp xúc giữa cốt thép và bê tông như hình 3.16. Giả thiết chiều 
dày của phần tử tiếp xúc thứ i là t thì biến dạng trượt của phần tử có dạng: 
γi =
Δi
t
=
1
t
[NΔ1(𝑢1 − 𝑦𝑖𝜃1 − 𝑢𝑠1) + NΔ2(𝑢2 − 𝑦𝑖𝜃2 − 𝑢𝑠2)]
(3.27) 
Từ đó, luận án đã xác định được ma trận biến dạng của 3 loại phần tử bê 
tông, phần tử cốt thép và phần tử tiếp xúc trong phần tử dầm BTCT. Thay các 
biểu thức của chuyển vị và biến dạng vào phương trình cân bằng [115], ta nhận 
được phương trình cân bằng tĩnh cho bài toán biến dạng bé và phi tuyến vật lý: 
𝑃(𝜎) = 𝑓 (3.30) 
trong đó P() và f tương ứng là véc tơ ứng lực và véc tơ tải trọng ngoài: 
𝑃 = ∑ 𝑃𝑒(𝜎)𝑒 ; 𝑃
𝑒(𝜎) = ∫ 𝐵𝑇𝜎𝑑𝑉
𝑉𝑒
; (3.31) 
𝑓 = ∑ 𝑓𝑒𝑒 ; 𝑓
𝑒 = ∫ 𝑁𝑇𝑏𝑑𝑉
𝑉𝑒
+ ∫ 𝑁𝑇𝑡̅𝑑𝑆
𝑆𝑒
; (3.32) 
Trường hợp đàn hồi tuyến tính  = D, ta nhận được: 
𝑓(𝜎) = (∫ 𝐵𝑇𝐷𝐵𝑑Ω
Ω
) �̃� = 𝐾�̃�; (3.33) 
trong đó K gọi là ma trận độ cứng của phần tử. 
Luận án sử dụng phương pháp Newton – Raphson cải tiến để giải (3.30). 
Hình 3.18. Chia thớ mặt cắt ngang của tiết diện thanh 
Ứng suất tại mỗi thớ (hình 3.18) của phần tử bê tông tính theo đường 
cong ứng suất biến dạng của bê tông (hình 3.10). Giả thiết ứng suất trong cốt 
thép phân bố tuyến tính 𝜎𝑠 = 𝜎𝑠1 +
𝜎𝑠2−𝜎𝑠1
𝐿
𝑥 với 𝜎𝑠1 là ứng suất tại điểm đầu và 
𝜎𝑠2 là ứng suất tại điểm cuối của phần tử như hình 3.12. Tương tự, giả thiết ứng 
y
x
b
h

Aci
yi
ci
M
y
x
b
h

Aci
yi
ci
M
N

0
Asi Asi
12 
suất trong phần tử tiếp xúc phân bố tuyến tính có dạng 𝜏𝑠 = 𝜏𝑠1 +
𝜏𝑠2−𝜏𝑠1
𝐿
𝑥. 
3.6. Xây dựng chương trình tính toán dầm bê tông cốt thép bị ăn mòn 
Hình 3.19. Sơ đồ khối chương trình CBS tính dầm BTCT bị ăn mòn 
Xác định véc tơ ngoại lực mới nếu có pi 
Thực hiện các bước lặp thứ i 
Xác định phản lực của các phần tử trong kết cấu 
Tính toán tải trọng không cân bằng 
Thiết lập giá trị ban đầu cho số gia chuyển vị 
Tạo vòng lặp mới 
Thêm số gia chuyển vị 
Tính toán mô men dẻo của tiết diện 
Xác định phản lực của các phần tử trong kết cấu 
Tính toán tải trọng không cân bằng 
Thêm chuyển vị tính được vào chuyển vị bước trước 
Xây dựng ma trận độ cứng các phần tử của hệ 
Không hội tụ 
Hội tụ 
Tính toán sai số 
Kết thúc 
Bắt đầu 
Số gia chuyển vị j 
13 
Luận án đã xây dựng được một chương trình tính toán cho dầm BTCT bị 
ăn mòn với sơ đồ khối trên hình 3.19. Chương trình CBS sử dụng các mô hình 
vật liệu của bê tông trên hình 3.10, cốt thép trong hình 3.11b, ăn mòn cốt thép 
trên hình 3.2 và quan hệ lực bám dính đối với cốt thép như hình 3.3. 
Trong quá trình tính toán, tải trọng tác dụng lên dầm (không bị ăn mòn 
hay bị ăn mòn) được giả thiết là tăng từ từ cho đến khi cốt thép chịu kéo tại tiết 
diện nguy hiểm bị chảy dẻo hoàn toàn, tương ứng với dạng phá hoại dẻo hay 
dạng phá hoại 1 trên hình 3.8. 
Khi tính toán cốt thép bị ăn mòn, chương trình cũng giả thiết các thanh 
cốt thép bị ăn mòn là đều theo chiều dài thanh với giá trị ăn mòn là giá trị trung 
bình [55]. Việc xem xét mức độ ăn mòn khác nhau trên từng phần tử hay trên 
phạm vi nhỏ hơn vượt ra ngoài phạm vi nghiên cứu của luận án. 
Để đơn giản cho mô phỏng ứng xử của dầm, ta có thể xem mức độ ăn mòn 
trung bình của cốt thép chịu kéo và chịu nén là tương tự nhau. Trường hợp 
không có dữ liệu thí nghiệm, ta giả thiết lực bám dính của các thanh thép bị ăn 
mòn giảm tới 65% lực bám dính max [89, 90]. 
Đối với cốt thép chịu kéo bị ăn mòn thì mối quan hệ ứng suất và liên kết 
bám dính bị thu nhỏ lại bởi hệ số 0,65. Đối với cốt thép chịu nén bị ăn mòn, 
đường cong ứng suất và liên kết bám dính ban đầu không thay đổi. 
Chương trình được lập có xét đến các trường hợp dầm bê tông không có 
cốt đai và có cốt đai: 
- Khi không có cốt thép đai thì chọn cường độ bê tông tương ứng với bê 
tông không bị hạn chế nở hông (hình 3.3); 
- Do cốt thép đai chỉ ảnh hưởng đến cường độ của bê tông, tương đương 
với bê tông bị hạn chế nở hông, nên ta chỉ cần thay đồi cường độ bê tông từ số 
liệu nhập, không cần phải thay đổi chương trình. 
3.7. Kiểm tra độ tin cậy của chương trình tính toán 
Hình 3.20. Dầm đơn giản chịu tải thử nghiệm 
150 150800 400 800
PP
2
0
0
h
b
d
h=200
d=169
b=150
14 
Hình 3.25 là so sánh các kết quả tính toán đường cong quan hệ tải trọng 
và chuyển vị tại tiết diện giữa nhịp theo chương trình CBS, chương trình Ansys 
của Ali Ghods và kết quả thực nghiệm của Rodriguez và các cộng sự cho 
trường hợp dầm không bị ăn mòn (dầm D111), và dầm đã bị ăn mòn (dầm 
D115) nên phải xét đến sự suy giảm của lực bám dính giữa bê tông và cốt thép. 
Ta nhận thấy kết quả tính cho dầm đã bị ăn mòn theo chương trình CBS rất gần 
với kết quả tính toán bằng Ansys của Ali Ghods và kết quả thực nghiệm. Mặt 
khác, ta cũng nhận thấy rằng khi bị ăn mòn thì khả năng chịu tải trọng của dầm 
là giảm đáng kể. Như vậy, chương trình CBS là tin cậy, có thể dùng cho tính 
toán chuyển vị của dầm BTCT bị ăn mòn với sai số nhỏ, chấp nhận được 
Hình 3.25. So sánh kết quả tính của dầm 
bị ăn mòn (dầm D115) 
Hình 3.26. Biểu đồ quan hệ mô men 
và góc xoay tại tiết diện giữa nhịp 
Hình 3.26 là biểu đồ quan hệ mô men và góc xoay tại tiết diện giữa nhịp 
theo chương trình CBS để xác định khả năng chịu lực của dầm D115. Ta nhận 
thấy khả năng chịu mômen uốn còn lại của dầm theo kết quả thực nghiệm là 
11,6kNm [89, 90], trong khi kết quả tính theo chương trình CBS là 12,03kNm. 
Như vậy, sai số tính toán so với kết quả thực nghiệm là 3,5%. 
3.8. Ảnh hưởng của sự suy giảm đường kính cốt thép và lực bám dính 
Hình 3.27 thể hiện kết quả khảo sát ảnh hưởng của sự suy giảm đường 
kính cốt thép bị ăn mòn, trong đó giả thiết ăn mòn là đều dọc thanh, đến khả 
năng chịu tải trọng của dầm BTCT theo chương trình CBS với các trường hợp 
suy giảm đường kính cốt thép từ 3% đến 15%. Ta nhận thấy rằng, sự suy giảm 
đường cốt thép làm giảm đáng kể đến khả năng chịu tải của dầm: khi đường 
kính cốt thép giảm 3% thì khả năng chịu lực của dầm giảm 11,93% so với 
trường hợp không bị ăn mòn; khi đường kính cốt thép giảm 15% thì khả năng 
chịu tải của dầm giảm 23,8% so với trường hợp không bị ăn mòn. 
0
5
10
15
20
25
30
35
40
45
0 0.01 0.02 0.03 0.04 0.05
Ket qua TN (D115)
ANSYS của Ali Ghods (D 115)
ATENA (D115)
CBS (D115)T
ải
 t
rọ
n
g
 (
k
N
)
Chuyển vị giữa nhịp của dầm (m)
0
2
4
6
8
10
12
14
0 0.01 0.02 0.03 0.04 0.05 0.06
M
ô
 m
en
 (
k
N
.m
)
Góc xoay (Rad/m)
15 
Hình 3.28 thể hiện kết quả khảo sát ảnh hưởng của sự suy giảm lực bám 
dính giữa cốt thép và bê tông khi bị ăn mòn đến khả năng chịu tải trọng của 
dầm BTCT theo chương trình CBS với các trường hợp max=4.5MPa; 5,5MPa; 
...; 7MPa. Ta nhận thấy khi lực bám dính bị suy giảm mạnh thì ảnh hưởng rất 
lớn đến khả năng chịu lực của dầm BTCT. 
 Hình 3.27. Kết quả tính khi đường 
kính cốt thép thay đổi 
Hình 3.28. Kết quả tính khi lực bám 
dính thay đổi 
3.9. Kết luận chương 3 
1. Khi dầm BTCT bị ăn mòn thì các tham số như đường kính cốt thép Φ, 
lực bám dính max là tham số khó có thể đo đạc được. Khi mức độ ăn mòn trên 
2,5% có thể coi Φ, max không có mối quan hệ, là hai biến độc lập. Khi không 
có số liệu thực nghiệm thì có thể lấy max trong khoảng 65%-80%. Đây là cơ sở 
lựa chọn biến và miền biến thiên của biến chẩn đoán. 
2. Xây dựng được thuật toán và chương trình CBS, khảo sát sự ảnh hưởng 
của sự suy giảm Φ, max. Chương trình đảm bảo tin cậy, sai số chấp nhận được. 
CHƯƠNG 4. CHẨN ĐOÁN DẦM BÊ TÔNG CỐT THÉP BỊ ĂN MÒN 
TRONG TRƯỜNG HỢP THIẾU SỐ LIỆU 
4.1. Mở đầu 
Quy trình hiện nay về đánh giá khả năng chịu lực còn lại của kết cấu 
BTCT bị ăn mòn chưa đáp ứng được bài toán thực tế đặt ra trong trường hợp 
thiếu số liệu. Dưới đây, luận án sẽ kết hợp những kết quả đạt được của chương 
2 và chương 3, để xây dựng một sơ đồ khối giải bài toán chẩn đoán cho dầm 
BTCT bị ăn mòn. Độ tin cậy của thuật toán được kiểm chứng thông qua việc so 
sánh các kết quả tính toán theo thuật toán của luận án với kết quả thực nghiệm 
của Rodriguez et al. [89, 90] và của Mangatet al. [79], từ đó rút ra nhận xét và 
kết luận về các kết quả đạt được. 
0
5
10
15
20
25
30
35
40
45
0 0.01 0.02 0.03 0.04 0.05
Đường kính giảm 3%
Đường kính giảm 5%
Đường kính giảm 9%
Đường kính giảm 12%
Đường kính giảm 15%
Chuyển vị giữa nhịp của dầm (m)
T
ải
 t
rọ
n
g
 (
k
N
)
0
5
10
15
20
25
30
35
40
45
50
0 0.01 0.02 0.03 0.04 0.05
Tmax = 7.0Mpa
Tmax = 6.5Mpa
Tmax = 5.5Mpa
Tmax = 4.5Mpa
Chuyển vị giữa nhịp của dầm (m)
T
ải
 t
rọ
n
g
 (
k
N
)
16 
4.2. Khảo sát chi tiết các tham số trên dầm bê tông cốt thép bị ăn mòn 
Yêu cầu khảo sát là thu được các số liệu về tình trạng hư hỏng của kết 
cấu, cụ thể là lượng hóa bằng số liệu và bằng hình ảnh những vấn đề sau: 
- Sai lệch kích thước hình học của kết cấu; 
- Chất lượng bê tông thể hiện qua cường độ bê tông; 
- Biến dạng kết cấu thể hiện qua độ võng kết cấu; 
- Các đặc trưng vết nứt như số lượng, chiều rộng, chiều dài, chiều sâu và 
hướng vết nứt; 
- Mức độ ăn mòn hay mức độ rỉ cốt thép. 
Một số vấn đề tồn tại trong việc đánh giá kết cấu: 
- Xác định cường độ của bê tông đòi hỏi một số lượng mẫu đủ lớn để 
thống kê. Ngược lại nếu số lượng mẫu không đủ lớn dẫn đến kết quả sai số lớn; 
- Xác định đường kính thực còn lại của cốt thép là rất khó, nên chỉ có thể 
dự báo biến thiên trong một khoảng nào đó.; 
- Cốt thép bị ăn mòn, khó có thể xác định được max. Do vậy, khi tính toán 
khả năng chịu lực thường coi là bám dính tuyệt đối. 
4.3. Quy trình cơ bản chẩn đoán dầm bê tông cốt thép bị ăn mòn 
Hình 4.1. Mô hình tổ hợp khả dĩ của 1 với các biến ngẫu nhiên 
Hình 4.2. Mô hình tổ hợp khả dĩ của (ϕ1, ϕ2,  , ϕn) với các biến ngẫu nhiên 
0 
f f cc 
0 a2 b2 0
a3 b3f cc max
1
a1 b1
f( max)
f
ccj

maxj
0 
f f cc 
0 a2 b2 0 a3 b3f cc maxa1 b1
f( max)
f
ccj

maxj
i
17 
1. Xác định biến chẩn đoán: Chọn biến chẩn đoán là đường