Tóm tắt Luận án Nghiên cứu xác định trạng thái ứng suất ban đầu của đất đá và sự thay đổi của trạng thái ứng suất này khi có CTN

Trang 1

Trang 2

Trang 3
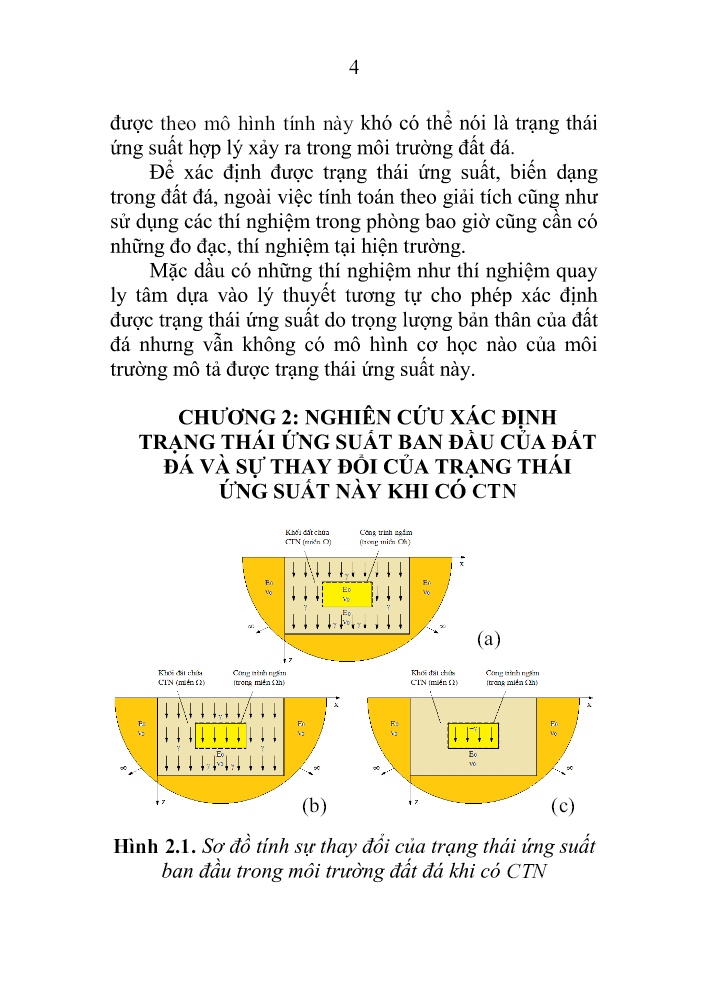
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Tóm tắt Luận án Nghiên cứu xác định trạng thái ứng suất ban đầu của đất đá và sự thay đổi của trạng thái ứng suất này khi có CTN", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Tóm tắt Luận án Nghiên cứu xác định trạng thái ứng suất ban đầu của đất đá và sự thay đổi của trạng thái ứng suất này khi có CTN

g thái ứng suất do trọng lượng bản thân của đất đá nhưng vẫn không có mô hình cơ học nào của môi trường mô tả được trạng thái ứng suất này. CHƢƠNG 2: NGHIÊN CỨU XÁC ĐỊNH TRẠNG THÁI ỨNG SUẤT BAN ĐẦU CỦA ĐẤT ĐÁ VÀ SỰ THAY ĐỔI CỦA TRẠNG THÁI ỨNG SUẤT NÀY KHI CÓ CTN Hình 2.1. Sơ đồ tính sự thay đổi của trạng thái ứng suất ban đầu trong môi trường đất đá khi có CTN (a) (b) (c) 5 Nội dung chủ yếu của chương này trình bày phương pháp xây dựng bài toán xác định trạng thái ứng suất ban đầu của đất đá bdi,jσ -(hình 2.1b) và trạng thái ứng suất khi chỉ xét trọng lượng bản thân khối đất đá trong khu vực xây dựng CTN -γi,jσ -(hình 2.1c) dựa trên nguyên lý thế năng biến dạng cực tiểu Castigliano nghĩa là sử dụng ứng suất làm ẩn. 2.2. Sử dụng nguyên lý thế năng biến dạng cực tiểu (NLTNBDCT) để xây dựng các phƣơng trình cân bằng (PTCB) Trong nội dung dưới đây chỉ trình bày mô hình môi trường đàn hồi tuyến tính và mô hình môi trường cực tiểu ứng suất tiếp lớn nhất. Trong luận án còn xét thêm mô hình môi trường đàn hồi không xét biến dạng ngang ( = 0) và mô hình môi trường đàn hồi có hệ số áp lực ngang K0 = ν 1 - ν . 2.2.1. Mô hình môi trường đàn hồi tuyến tính (ĐHTT) Theo NLTNBDCT, bài toán tìm trạng thái ứng suất cân bằng trong môi trường được đưa về giải bài toán quy hoạch với hàm mục tiêu là thế năng biến dạng cực tiểu của môi trường đàn hồi được viết như sau: 2 2 2x z x z xz Ω σ σ1 min + -νσ σ + 1+ ν τ dΩ E 2 2 Z (2.9a) và các ràng buộc là 2 PTCB sau: x xz xz z σ τ 0 x z τ σ γ 0 x z (2.9b) 6 Bằng phương pháp thừa số Lagrange, sử dụng phép tính biến phân ta nhận được hệ 5 phương trình (2.12) đủ để tìm được 5 ẩn chưa biết của bài toán như dưới đây : x xz xz z x z z x xz z x x z σ τ 0 x z τ σ γ 0 x z 1 u σ - νσ = = E x 1 w σ - νσ = = E z E u w τ = Gε 2 1+ ν x ε ε z (2.12) 2.2.4. Mô hình môi trường cực tiểu ứng suất tiếp lớn nhất (ƯSTLN) Tương tự như trên, ta có bài toán tìm trạng thái ứng suất cân bằng trong môi trường được đưa về giải bài toán quy hoạch với hàm mục tiêu là thế năng biến dạng cực tiểu của ứng suất tiếp lớn nhất được viết như sau : Hàm mục tiêu: 2 2x z Ω xz Ω σ - σ1 Z = + τ dΩ min G 2 (2.23) Với ràng buộc là hai PTCB được viết theo biểu thức (2.9b) như đã trình bày ở trên. Biến đổi tương tự như trên, ta cũng nhận được hệ 5 phương trình (2.26) như trình bày dưới đây : 7 x z x xz xz z x z z x xz xz σ τ 0 x z τ σ γ 0 x z 1 u σ -σ 2G x 1 w σ -σ 2G z G u w G τ = ε 2 x 2 ε ε z (2.26) Như vậy, bằng cách sử dụng nguyên lý thế năng biến dạng cực tiểu, các phương trình cân bằng và sử dụng phép tính biến phân ta không chỉ nhận được đầy đủ hệ phương trình vi phân cân bằng để xác định trạng thái ứng suất trong môi trường mà còn nhận được các liên hệ giữa ứng suất và biến dạng của môi trường. 2.3. Xác định trạng thái ứng suất (TTƢS) ban đầu trong môi trƣờng đất đá (MTĐĐ) do trọng lƣợng bản thân (TLBT) và sự thay đổi của trạng thái ứng suất này khi có CTN 2.3.1. Mô hình môi trường đàn hồi tuyến tính Bài toán xác định bdi,jσ Được đưa về giải bài toán quy hoạch với hàm mục tiêu là thế năng biến dạng cực tiểu của vật thể được viết theo biểu thức (2.27a) – biểu thức nhận được bằng cách thay E=E0 ; =0 vào biểu thức (2.9a) và các ràng buộc là hai PTCB được xét với toàn bộ môi trường đất đá có CTN ( miÒn Ω ) được biểu diễn như dưới đây : 8 σ τ τ σ γ x xz xz z t trong miÒn 0 XÐ x z 0 XÐ x t trong miÒn z Ω Ω (2.27b) Bài toán xác định -γi,jσ Tương tự ta cũng đưa về giải bài toán quy hoạch với hàm mục tiêu là thế năng biến dạng cực tiểu của vật thể được viết theo biểu thức (2.27a) và các ràng buộc là các PTCB (2.28) được viết như sau : σ τ τ σ τ σ γ x xz xz z xz z t trong miÒn t trong 0 XÐ x z miÒn h t trong miÒn 0 XÐ x z 0 XÐ x z h Ω Ω -Ω Ω (2.28) Hiệu của nghiệm hai bài toán trên cho ta trường ứng suất trong môi trường đất đá khi có CTN 0i,jσ . 2.3.4. Mô hình môi trường cực tiểu ƯSTLN Bài toán xác định bdi,jσ Tương tự như trên, ta có bài toán được đưa về giải bài toán quy hoạch với hàm mục tiêu là thế năng biến dạng cực tiểu của ứng suất tiếp lớn nhất được viết theo biểu thức (2.23) và các ràng buộc là hai PTCB được xét với toàn bộ môi trường đất đá có CTN ( miÒn Ω ) được viết theo biểu thức (2.27b). 9 Bài toán xác định -γi,jσ Tương tự như trên, bài toán được đưa về giải bài toán quy hoạch với hàm mục tiêu được viết theo biểu thức (2.23) và các ràng buộc được viết theo biểu thức (2.28). Hiệu của nghiệm hai bài toán trên cho ta trường ứng suất trong môi trường đất đá khi có CTN 0i,jσ . Trong nội dung của luận án còn xét thêm mô hình môi trường đàn hồi không xét biến dạng ngang ( = 0) và mô hình môi trường đàn hồi có hệ số áp lực ngang K0 = ν 1 - ν . 2.5. Khảo sát số Trong môi trường Matlab, tác giả đã xây dựng các chương trình tính để xác định trạng thái ứng suất ban đầu trong đất đá do trọng lượng bản thân và sự thay đổi trạng thái ứng suất này khi có CTN (khối đất đá trong CTN vẫn còn độ cứng) như sau: + Chương trình TS1 – Xác định trạng thái ứng suất ban đầu của đất đá với mô hình môi trường cực tiểu ứng suất tiếp lớn nhất; + Chương trình ES1 – Xác định trạng thái ứng suất ban đầu của đất đá với mô hình môi trường đàn hồi tuyến tính; + Chương trình ES2 – Xác định trạng thái ứng suất ban đầu của đất đá với mô hình môi trường đàn hồi có hệ số áp lực ngang K0 = 1 ; 10 + Chương trình TSh1 – Xác định trạng thái ứng suất của đất đá khi không xét trọng lượng bản thân khối đất đá trong công trình ngầm với mô hình môi trường cực tiểu ứng suất tiếp lớn nhất; + Chương trình ESh1 – Xác định trạng thái ứng suất của đất đá khi không xét trọng lượng bản thân khối đất đá trong công trình ngầm với mô hình môi trường đàn hồi tuyến tính; + Chương trình ESh2 – Xác định trạng thái ứng suất của đất đá khi không xét trọng lượng bản thân khối đất đá trong công trình ngầm với mô hình môi trường đàn hồi có hệ số áp lực ngang K0 = 1 ; Trong luận án, tác giả khảo sát khối đất có kích thước (9x9)m, được rời rạc thành 324 phần tử kích thước (0,5x0,5)m. Khối đất có E0 = 10 MPa, 0 = 0,3, = 20 kN/m 3 . Để đơn giản cho lập trình tính toán, lấy ví dụ trong khối đất có hầm tiết diện hình vuông (3x3)m, như hình vẽ 2.10 dưới đây. Hình 2.10. Sơ đồ rời rạc hóa khối đất có CTN 11 Dưới đây trình bày sự phân bố ứng suất ban đầu σz , σx trong khối đất tính toán và ứng suất σz , σx trong khối đất khi không xét trọng lượng bản thân khối đất trong CTN với mô hình cực tiểu ƯSTLN và mô hình ĐHTT. Các mô hình môi trường khác được trình bày trong luận án. Kết quả phân bố ứng suất ban đầu trong khối đất tính toán được thể hiện trên các hình vẽ dưới đây: 0.02 0.02 0.02 0.04 0.04 0.04 0.06 0.06 0.06 0.08 0.08 0.08 0.1 0.1 0.1 0.12 0.12 0.12 0.14 0.14 0.14 0.16 0.16 0.16 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 2.11. Trường ƯS σz (MPa) - (cực tiểu ƯSTLN) 0 00.0 1 0.01 0.01 0 .0 1 0 .0 2 0.02 0.02 0.02 0 .0 3 0.03 0.03 0.03 0 .0 3 0 .0 4 0.04 0.04 0 .0 4 0 .0 4 0 .0 4 0 .0 4 0 .0 5 0 .0 5 0 .0 5 0.05 0.0 5 0 .0 5 0 .0 5 0. 05 0.06 0 .0 6 0.06 0.0 6 0 .0 6 0. 06 0.07 0.07 0.07 0. 07 0. 07 0.08 0.08 0.08 0. 08 0. 08 0.09 0. 090.1 0. 1 0.11 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 2.12. Trường ƯS σz (MPa) - (ĐHTT) 0 0 0 0 0 0 0 0 0.02 0.02 0.02 0.04 0.04 0.04 0.06 0.06 0.06 0.08 0.08 0.08 0.1 0.1 0.1 0.12 0.12 0.12 0.14 0.14 0.14 0.16 0.16 0.16 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 2.17. Trường ƯS σx (MPa) - (cực tiểu ƯSTLN) -0.03 -0 .03-0.02 -0 .02-0.01 -0 .0 1 0 0 0 .0 1 0.01 0 .0 1 0.01 0.02 0.02 0. 02 0.02 0.02 0.02 0.02 0.02 0.03 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 2.18. Trường ƯS σx (MPa) - (ĐHTT) x (m) z (m ) 0 x (m) z (m ) 0 x (m) z (m ) 0 x (m) z (m ) 0 12 Trong luận án còn trình bày trường ứng suất ban đầu σz , σx , xz khi mở rộng khối đất tính toán theo chiều sâu và chiều rộng để thấy rõ việc thỏa mãn điều kiện vô hạn của bài toán. Kết quả phân bố ứng suất của trong khối đất khi không xét trọng lượng bản thân khối đất trong CTN được thể hiện trên các hình vẽ dưới đây: 0.02 0.02 0.02 0.04 0.04 0.04 0.06 0.06 0.06 0.08 0.0 8 0.08 0.08 0.1 0.1 0.1 0.1 0.12 0.12 0.12 0.14 0.14 0.14 0.1 6 0.16 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 2.29. Trường ƯS σz (MPa) - (cực tiểu ƯSTLN) 0 0 0 .0 0 5 0 .0 0 5 0.005 0.005 0.00 5 0 .0 0 5 0 .0 0 5 0 .0 1 0 .0 1 0.01 0.01 0 .0 1 0 .0 1 0 .0 10.015 0 .0 1 5 0 .0 1 5 0.015 0 .0 1 5 0 .0 1 5 0.02 0.02 0.02 0. 02 0. 02 0.02 0 .0 2 0.02 0 .0 2 0.025 0.025 0. 02 5 0.025 0.025 0 .0 2 5 0.03 0.03 0. 03 0.03 0.0 3 0. 03 0.035 0.035 0. 03 5 0.035 0.035 0.04 0.04 0.0 4 0.045 0.0 450.05 0.050.055 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 2.30. Trường ƯS σz (MPa) - (ĐHTT) 0 0 0.02 0.02 0.02 0.04 0.04 0.04 0.06 0.06 0.06 0.08 0.08 0.08 0.1 0.1 0.1 0.12 0.12 0.12 0.14 0.14 0.14 0.16 0.16 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 2.32. Trường ƯS σx (MPa) - (cực tiểu ƯSTLN) -0.04 -0 .0 4 -0.02 -0. 02 0 0 0 0 0 0 0 0 0 0.02 0.02 0.02 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 2.33. Trường ƯS σx (MPa) - (ĐHTT) Trong luận án cũng trình bày trường ứng suất σz , σx , xz trong khối đất khi không xét trọng lượng bản thân x (m) z (m ) 0 x (m) z (m ) 0 x (m) z (m ) 0 x (m) z (m ) 0 13 khối đất trong CTN khi mở rộng khối đất tính toán theo chiều sâu và chiều rộng để thấy rõ điều kiện khối đất nằm trong môi trường vô hạn cũng sẽ được thỏa mãn. Từ kết quả khảo sát trên nhận thấy đối với mô hình môi trường cực tiểu ứng suất tiếp lớn nhất bảo đảm hợp logic với điều kiện tải trọng và điều kiện vô hạn của khối đất tính toán hơn cả bởi ta nhận được trường ứng suất ban đầu σz = σx = γ.h, xz= 0. Còn đối với mô hình môi trường đàn hồi không nhận được kết quả như vậy. CHƢƠNG 3: XÂY DỰNG BÀI TOÁN TƢƠNG TÁC GIỮA CÔNG TRÌNH NGẦM VÀ MÔI TRƢỜNG ĐẤT ĐÁ Trong chương này trình bày phương pháp xây dựng bài toán xác định trạng thái ứng suất, biến dạng của đất đá xung quanh CTN có các dạng kết cấu chống đỡ khác nhau. Trong luận án, xét trường hợp kết cấu chống đỡ là các thanh chống đứng và các thanh chống ngang; kết cấu chống đỡ là khung có liên kết ngàm và khung có liên kết khớp ở 4 góc. Mô hình môi trường khảo sát là cực tiểu ứng suất tiếp lớn nhất và đàn hồi tuyến tính. Khi lấy hoàn toàn khối đất đá ra khỏi CTN, để tránh sụt lở, sụp đổ hoặc phá hỏng thì ta cần thay bằng các kết cấu chống đỡ, áp lực của MTĐĐ sẽ tác dụng trực tiếp lên kết cấu chống đỡ này và kết cấu chống đỡ sẽ có phản lực lên đất đá, ta gọi đó là tương tác ứng suất. Vì các kết cấu chống đỡ CTN và MTĐĐ đều có chuyển vị, tùy thuộc vào tương quan độ cứng cho nên trên biên CTN ta có chuyển vị của kết cấu chống đỡ cũng phải bằng với chuyển vị của MTĐĐ, ta có tương tác chuyển vị. 14 Bài toán được xây dựng như sau: 3.1. Kết cấu chống đỡ là các thanh chống đứng và các thanh chống ngang Hình 3.1. Sơ đồ bài toán xác định TTƯS, chuyển vị trong MTĐĐ khi kết cấu chống đỡ CTN là các thanh chống đứng và các thanh chống ngang 3.1.1. Mô hình môi trường cực tiểu ƯSTLN Bài toán được đưa về giải bài toán quy hoạch với: Hàm mục tiêu : c c 2 2x z xz Ω-Ωh lz lx2 2n m zc xc zc xc i=1 i=1co co0 0 σ - σ1 + τ dΩ G 2 min σ σ1 1 + b dz + b dx E 2 E 2 Z (3.31a) Và ràng buộc là các PTCB tương tác ứng suất (3.31b) và tương tác chuyển vị (3.31c) được viết như dưới đây: (a) (b) 15 σ τ σ τ τ σ τ σ σ σ σ σ 0 0 x zx x zx 0 0 xz z xz z 0 xc x 0 zc z trong miÒn - h trong + = + x z x z + = + x z x z miÒn - h trong miÒn h tron = g m x x = z z iÒn h Ω Ω Ω Ω Ω Ω (3.31b) γ γ γ τ τ σ σ σ σ - xz xz - co xc x - co zc z trong miÒn - h trong miÒn - u w + =0 x z u w G + + = z x u 2E + = x w 2E + = h trong miÒn h trong miÒn z h Ω Ω Ω Ω Ω Ω (3.31c) 3.1.2. Mô hình môi trường ĐHTT Hàm mục tiêu : c c 2 2 2x z 0 x z 0 xz 0Ω-Ωh lz lx2 2n m zc xc zc xc i=1 i=1co co0 0 σ σ1 + - ν σ σ + 1+ ν τ dΩ E 2 2 min σ σ1 1 + b dz + b dx E 2 E 2 Z (3.30a) Với ràng buộc là các PTCB tương tác ứng suất (3.30b) được viết giống như biểu thức (3.31b) và tương tác chuyển vị (3.30c) được trình bày như dưới đây: 16 (a) (b) (c) γ γ γ γ γ ν σ σ ν ν ν σ σ ν ν τ τ ν σ σ σ σ -0 0 x x 0 0 -0 0 z z 0 0 -0 xz xz 0 - co xc x - co zc z 2E u u w + = 1+ x 1-2 x z 2E w u w + = 1+ z 1-2 x z E u w + = 1+ + + trong miÒn - h trong miÒn z x u 2E + = x w 2E h tr+ = o i z ng m Ω Ω Ω Òn hΩ (3.30c) 3.2. Kết cấu chống đỡ là hệ khung Hình 3.4. Sơ đồ bài toán xác định TTƯS, chuyển vị trong MTĐĐ khi kết cấu chống đỡ CTN là hệ khung 17 3.2.1. Mô hình môi trường cực tiểu ƯSTLN Tương tự như trên, bài toán được đưa về giải bài toán quy hoạch với: Hàm mục tiêu: 2 2x z xz Ω-Ωh lx lx lz lz2 2 2 2 x1 x2 z1 z2 co co co co0 0 0 0 σ - σ1 + τ dΩ G 2 min M M M M + dx+ dx+ dz+ dz 2E I 2E I 2E I 2E I Z (3.33a) Và các ràng buộc là các PTCB tương tác ứng suất (3.33b) và tương tác chuyển vị (3.33c) được trình bày như dưới đây: σ τ σ τ τ σ τ σ σ σ σ σ 0 0 x zx x zx 0 0 xz z xz z 2 0x1 z12 2 0x2 z22 2 0z1 x12 2 0z2 x22 + = + x z x z + = + x z x z d M + =0 dx d M + = trong miÒn - h trong miÒn - h trong miÒn h trong miÒn h t 0 dx d M + =0 dz d M + rong miÒn h trong miÒn h=0 dz Ω Ω Ω Ω Ω Ω Ω Ω (3.33b) 18 γ γ γ γ τ τ σ σ σ σ σ σ - xz xz - 2 i,j x1 co0 2 i,j - 2 i,j x2 co0 2 i,j - i,j z1 0 i,j trong miÒn - h trong miÒn - h trong miÒn h trong miÒn u w + =0 x z u w G + + = z x d w M 1 -2E I = 0 dx d w M 1 -2E I = 0 1 h dx M Ω Ω Ω Ω Ω Ω γσ σ 2 co 2 - 2 i,j z2 co0 2 i,j trong miÒn h t d u -2E I = 0 dz d u rong miM 1 -2E I = 0 d z Òn h Ω Ω (3.33c) 3.2.2. Mô hình môi trường ĐHTT Hàm mục tiêu: 2 2 2x z 0 x z 0 xz 0Ω-Ωh lx lx lz lz2 2 2 2 x1 x2 z1 z2 co co co co0 0 0 0 σ σ1 + - ν σ σ + 1+ ν τ dΩ E 2 2 min M M M M + dx+ dx+ dz+ dz 2E I 2E I 2E I 2E I Z (3.32a) Với ràng buộc là các PTCB tương tác ứng suất (3.32b) được viết giống với biểu thức (3.31b) và tương tác chuyển vị (3.32c) được viết như dưới đây: 19 γ γ γ γ ν σ σ ν ν ν σ σ ν ν τ τ ν σ σ -0 0 x x 0 0 -0 0 z z 0 0 -0 xz xz 0 - i,j x1 i,j + trong miÒn - h + trong mi 2E u u w + = 1+ x 1-2 x z 2E w u w + = 1+ z 1-2 x z E u w + = Òn - h trong miÒn - 1+ z x M h 1 Ω Ω Ω Ω Ω Ω γ γ γ σ σ σ σ σ σ 2 co0 2 - 2 i,j x2 co0 2 i,j - 2 i,j z1 co0 2 i,j - 2 i,j z2 co0 2 i,j d w -2E I = 0 dx d w M 1 -2E I = 0 dx d u M 1 -2E I = 0 dz d u M 1 trong miÒn h tr -2E I = 0 ong miÒn h trong miÒn h trong miÒn h dz Ω Ω Ω Ω (3.32c) CHƢƠNG 4: KHẢO SÁT TRẠNG THÁI ỨNG SUẤT, BIẾN DẠNG CỦA ĐẤT ĐÁ XUNG QUANH CTN VÀ KẾT CẤU CHỐNG ĐỠ CTN 4.1. Chƣơng trình tính Trong môi trường Matlab, tác giả đã xây dựng các chương trình tính sau: + Chương trình TSch1: Xác định ứng suất, chuyển vị của đất đá xung quanh CTN với mô hình môi trường cực tiểu ứng suất tiếp lớn nhất, kết cấu chống đỡ là các thanh chống đứng và các thanh chống ngang; 20 + Chương trình ESch1: Xác định ứng suất, chuyển vị của đất đá xung quanh CTN với mô hình môi trường đàn hồi tuyến tính, kết cấu chống đỡ là các thanh chống đứng và các thanh chống ngang; + Chương trình TSch2: Xác định ứng suất, chuyển vị của đất đá xung quanh CTN với mô hình môi trường cực tiểu ứng suất tiếp lớn nhất, kết cấu chống đỡ là khung ngàm; + Chương trình ESch2: Xác định ứng suất, chuyển vị của đất đá xung quanh CTN với mô hình môi trường đàn hồi tuyến tính, kết cấu chống đỡ là khung ngàm; + Chương trình TSch3: Xác định ứng suất, chuyển vị của đất đá xung quanh CTN với mô hình môi trường cực tiểu ứng suất tiếp lớn nhất, kết cấu chống đỡ là khung khớp; + Chương trình ESch3: Xác định ứng suất, chuyển vị của đất đá xung quanh CTN với mô hình môi trường đàn hồi tuyến tính, kết cấu chống đỡ là khung khớp; 4.2. Khảo sát các kết quả của bài toán Khảo sát khối đất có các thông số như mục 2.5 chương 2 (hình vẽ 2.10). Trong luận án trình bày kết quả phân bố ứng suất, chuyển vị của đất đá xung quanh CTN có các dạng kết cấu chống đỡ khác nhau với mô hình cực tiểu ƯSTLN và ĐHTT. Dưới đây chỉ trình bày kết quả phân bố ứng suất, chuyển vị của đất đá xung quanh CTN có kết cấu chống đỡ là các thanh chống đứng và các thanh chống ngang và kết cấu chống đỡ là khung ngàm với mô hình cực tiểu ƯSTLN. 4.2.1. Bài toán 1: Kết cấu chống đỡ là các thanh chống đứng và các thanh chống ngang 21 x (m) z (m ) 0 x (m) z (m ) 0 Trường hợp mô đun đàn hồi của các thanh chống Eco=10 3 MPa, lớp đất phía trên CTN dày 3m, ta có: 0.02 0.02 0.02 0 .0 2 0 .0 2 0.02 0.04 0.04 0.04 0.04 0.0 4 0.04 0.06 0 .0 6 0.06 0 .0 6 0.06 0.06 0.06 0.08 0.08 0 .0 8 0.08 0.1 0.1 0.1 0.1 0.12 0.1 2 0.12 0.14 0.14 0 .14 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 4.3. Trường ứng suất σz (MPa) 0 0 0.02 0.02 0.02 0 .0 2 0 .0 2 0.02 0.04 0.04 0 .04 0.04 0.0 4 0.04 0.06 0 .0 6 0.06 0 .0 6 0.06 0.08 0.08 0 .0 8 0.08 0.1 0.1 0.1 0 .1 0 .1 0.12 0.12 0.12 0.14 0.14 0.14 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 4.4. Trường ứng suất σx (MPa) -0. 3 -0 .3 -0 .3 -0.3 -0 .2 -0 .2 -0 .2 -0 .2 -0 .2 -0.2 -0 .1 -0 .1 -0.1 -0 .1 -0 .1 -0 .1 -0 .1 -0 .1 -0 .1 -0 .1 0 0 0 0 0 0 0.1 0 .1 0 .1 0.1 0. 1 0 .1 0 .1 0. 1 0. 2 0 .2 0.2 0 .2 0.2 0 .3 0 .3 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 4.5. Trường chuyển vị đứng (cm) -0 .2 -0.15 -0.15 -0.1 -0.1 -0.1 -0.1 -0 .1 -0.1 -0.05 -0.05 -0.05 -0.0 5 -0 .0 5 -0.0 5 -0.05 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0.05 0.05 0. 05 0.05 0.05 0.05 0.0 5 0 .1 0. 1 0.1 0.1 0.1 0.1 0.15 0.15 0.2 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 Hình 4.6. Trường chuyển vị ngang (cm) 0 5 10 -0.01 -0.005 0 0.005 0.01 0.015 0.02 0.025 0 5 10 -0.01 -0.005 0 0.005 0.01 0.015 0.02 0 5 10 -0.01 -0.005 0 0.005 0.01 0.015 0.02 0.025 Hình 4.7. Ứng suất trong các thanh đứng (MPa) 1 2 3 4 5 6 7 -2 0 2 x 10 -3 1 2 3 4 5 6 7 -2 0 2 x 10 -4 1 2 3 4 5 6 7 -2 0 2 x 10 -3 Hình 4.8. Ứng suất trong các thanh ngang (MPa) x (m) z (m ) 0 x (m) z (m ) 0 22 4.2.3. Bài toán 3: Kết cấu chống đỡ là khung ngàm Trường hợp các dầm khung có mô đun đàn hồi Eco=10 4 MPa, chiều cao dầm khung hd = 20cm, lớp đất phía trên công trình
File đính kèm:
 tom_tat_luan_an_nghien_cuu_xac_dinh_trang_thai_ung_suat_ban.pdf
tom_tat_luan_an_nghien_cuu_xac_dinh_trang_thai_ung_suat_ban.pdf

