Tóm tắt Luận án Ứng dụng mạng nơron nhân tạo trong xử lý cấp 2 tin tức ra đa

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
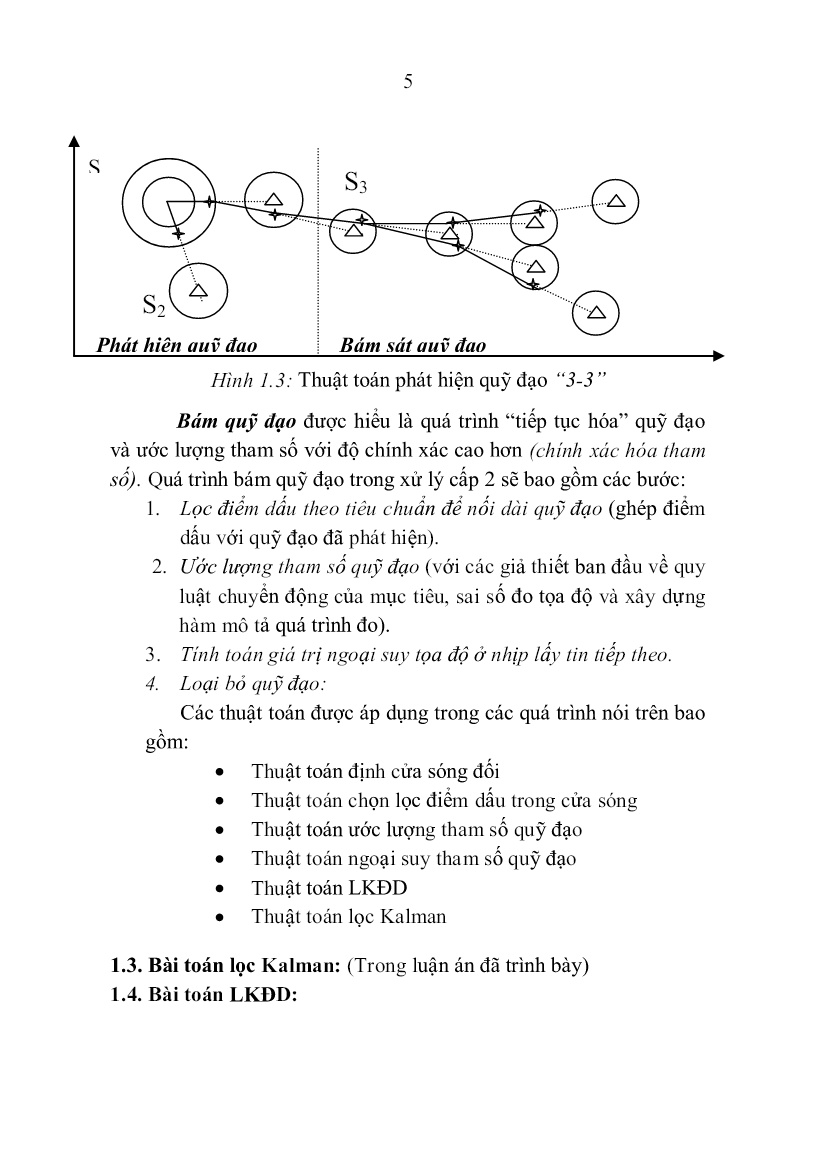
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Tóm tắt Luận án Ứng dụng mạng nơron nhân tạo trong xử lý cấp 2 tin tức ra đa", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Tóm tắt Luận án Ứng dụng mạng nơron nhân tạo trong xử lý cấp 2 tin tức ra đa

à hàm hợp lý cho mỗi tín hiệu điểm dấu và đƣợc tính theo công thức (1.44) trong luận án bản đầy đủ. 1.4.2.3 Thuật toán LKĐD theo xác suất đồng thời (JPDA) 𝑃 Ψ |𝑍 = 1 𝑐 𝜆𝑚 𝑘 −𝑇 𝑝𝑗 𝑡(𝑘) 𝑇 𝑡=1 (1.46) với 𝑝𝑗 𝑡(𝑘) là hàm hợp lý cho mỗi tín hiệu điểm dấu và đƣợc tính theo công thức (1.47). Kết luận Chƣơng 1 Từ những vấn đề nghiên cứu đã trình bày trong Chƣơng 1, ta rút ra các kết luận sau đây: - Mô hình HTRĐ liên kết thị tần đƣợc xây dựng từ các đài ra đa độc 8 lập có ý nghĩa kỹ thuật và thực tiễn rất lớn đối với điều kiện tác chiến hiện đại. - Việc sắp xếp dữ liệu điểm dấu, xác định chúng bằng các thuật toán và tiêu chuẩn xem chúng thuộc quỹ đạo mục tiêu nào là nội dung cơ bản của LKĐD. - Lọc Kalman mà cơ sở toán học chính của nó là lý thuyết ƣớc lƣợng thống kê là công cụ quan trọng trong giải bài toán xử lý cấp 2. - Từ các nghiên cứu nói trên ta thấy ràng, LKĐD và lọc Kalman là hai nội dung không thể tách rời trong xử lý cấp 2 tin tức ra đa . Từ những kết luận nêu trên, có thể giới hạn nội dung nghiên cứu "Ứng dụng công cụ mạng nơron nhân tạo trong xử lý cấp 2 tin tức ra đa" là: Tập trung vào thực hiện nhiệm vụ LKĐD - khâu quan trọng góp phần quyết định chất lƣợng các quá trình tiếp sau của lọc, bám quỹ đạo. CHƢƠNG 2 MẠNG NƠRON NHÂN TẠO VÀ ỨNG DỤNG MẠNG HOPFIELD TRONGXỬ LÝ CẤP 2 TIN TỨC RA ĐA 2.1. Tổng quát về mạng nơron nhân tạo: 2.1.1 Các khái niệm cơ bản về mạng nơron sinh học: Trên Hình 2.1 có mô tả cấu trúc và quan hệ trong nơron sinh học. Mạng nơron nhân tạo (Artificial Neuron Network-ANN) đƣợc xây dựng theo nguyên lý tổ chức và hoạt động tƣơng tự não ngƣời và đƣợc ứng dụng trong nhiều lĩnh vực khoa học khác nhau. Dạng tổng quát của nơron nhân tạo đƣợc vẽ trên Hình 2.2. Hình 2.1: Các quan hệ trong nơron sinh học S Vào Ra Nhân noron TruyÒn ph¸ t (action) Khí p thÇn kinh (synaps) w1 w2 w3 wn x1 x2 x3 xn i n i i w 1 xS Y=f(s) . . . đốt nhân Truyền phát action Truyền thu dendrite Khớp thần kinh synaps 9 Hình 2.2: Mô hình tổng quát nơron nhân tạo 2.2.Phân loại mạng nơron: 2.2.1. Mạng nơron truyền thẳng: 2.2.1.1 Mạng nơron nhân tạo một lớp: 2.2.1.2 Mạng nơron nhân tạo nhiều lớp: 2.2.1.3 Mạng nơron nhân tạo lan truyền ngược: 2.2.2. Mạng nơron phản hồi: 2.2.2.1 Mạng Hopfield: Hình 2.8: Mô hình mạng nơron Hopfield Xét mạng một lớp có mạch phản hồi gồm n đầu vào và m nơron (Hình2.8). Trong mỗi nơron thứ j đều có các tín hiệu lấy từ bên ngoài vào xj . Đáng chú ý là các tín hiệu đầu ra của nơron thứ j là yj đƣợc đƣa ngƣợc trở lại đầu vào của các nơron khác bởi trọng số wij, với i = 1,2,...,n và i ≠ 𝑗 (nghĩa là tín hiệu ra của mỗi nơron thứ i không đƣa ngƣợc trở lại đầu vào của chính nó wii=0). Trọng số của mạng có tính chất đối xứng: wij=wji. Tập các giá trị đầu ra iy của tất cả các nơron ở bƣớc thứ N nào đó sẽ tạo thành véctơ trạng thái NY của mạng. Mạng nhƣ vậy gọi là mạng Hopfield. Hàm năng lượng mạng Hopfield, Định lý Lyapunov: Cụ thể xem tài liệu [9] và luận án bản đầy đủ. . . . . . . . . . . . . . . . . x1 xj xn y1 yj yn wj1 w1j wnj w1n 10 2.2.2.2 Một số ứng dụng của mạng Hopfield: 1. Ứng dụng trong phân lớp và nhận dạng 2. Ứng dụng mạng Hopfield trong bài toán tối ƣu hóa: Nội dung bài toán nhƣ sau: Giả thiết rằng có n thành phố và đã biết khoảng cách giữa các thành phố đó. Nhiệm vụ của người bán hàng là phải thực hiện đi đến tất cả các thành phố đó với quãng đường ngắn nhất mà không phải lặp lại một thành phố quá một lần. Để giải quyết bài toán đã nêu, cách đặt vấn đề đơn giản nhất là liệt kê tất cả các đƣờng đi khả thi để tính toán tổng khoảng cách cho mỗi đƣờng đi và chọn đƣờng đi với quãng đƣờng ngắn nhất. Tuy nhiên nếu là n thành phố thì số đƣờng đi khả thi sẽ là n!/2n. Do vậy, dù là đơn giản, nhƣng cách đặt vấn đề nhƣ trên sẽ là không khả thi. Yêu cầu của bàn toán chỉ là xác định con đƣờng ngắn nhất nối một tập hữu hạn nào đó các thành phố với điều kiện mỗi thành phố chỉ đƣợc tính một lần. Đầu những năm 80 của thế kỷ trƣớc, ngay sau khi xây dựng xong mô hình mạng nơron mang tên mình, Hopfield đã cùng đồng nghiệp Tank [38] đã xây dựng cách tiếp cận giải bài toán TSP. Theo đó, để biểu diễn các hành trình có thể, hai nhà bác học đã đề xuất xây dụng một dạng ma trận đặc biệt, mà trong đó, các thành phố đƣợc thể hiện theo hàng. Còn cột sẽ phản ánh trình tự các thành phố trên đƣờng đi. Và ở tại vị trí nào đó của ma trận sẽ nhận giá trị là 1, nếu nhƣ thứ tự thành phố (ở cột tƣơng ứng) nằm trên đƣờng đi (ở hàng tƣơng ứng). Xét tổng quát, nếu giả thiết có n thành phố, thì sẽ có (n!/2n) phƣơng án đi. Và cần phải tìm trong số đó phƣơng án có quãng đƣờng ngắn nhất. Việc sử dụng hàm năng lƣợng và các điều kiện cực tiểu của nó đã cho phép giải bài toán trên một cách nhanh chóng. Sau khi tối thiểu hóa hàm năng lƣợng với các điều kiện ràng 11 buộc (xem tại trang 58 của Luận án bản đầy đủ), với số lƣợng các thành phố lần lƣợt là: 5,10,15,20,25 thì kết quả nhận đƣợc cùng với số lần lặp và thời gian hội tụ của mạng theo Bảng 2.1. Bảng 2.1: Kết quả nhận đƣợc tƣơng ứng với số lƣợng các thành phố Số thành phố Số lần lặp Thời gian(s) Kết quả 5 152 0.4652 Tốt 10 581 1.8075 Tốt 15 1021 3.2873 Tốt 20 2433 7.6458 Tốt 25 5292 16.2264 Chấp nhận đƣợc 2.3. Ứng dụng mạng Hopfield để giải bài toán LKĐD trong xử lý cấp 2 thông tin ra đa: 2.3.1 Sự liên quan giữa hai bài toán TSP và LKĐD ra đa: Vấn đề tìm kiếm xác suất 𝛽𝑥 𝑖 (𝑘) từ tỷ số hợp lý 𝜌𝑥 𝑖 (k) có các đặc tính giống nhƣ ở bài toán TSP. Nếu các điện áp đầu ra của mạng nơron đƣợc coi là các xác suất liên kết thì các cột có thể biểu diễn các quỹ đạo của mục tiêu trong khi các hàng có thể biểu diễn các điểm dấu. Khi đó mạng đƣợc thiết kế với đầu vào là các hàm hợp lý chuẩn hóa, đầu ra là các giá trị xác suất liên kết giữa quỹ đạo và các điểm dấu. Bằng việc xem xét các đặc tính của JPDA, ta thấy rằng bài toán TSP và JPDA có những điểm tƣơng đồng nhƣ sau: - Về bản chất đều là bài toán tối ƣu với các điều kiện ràng buộc ban đầu. Trong bài toán TSP phải lựa chọn cách đi để quãng đƣờng đi là ngắn nhất (lựa chọn thứ tự các thành phố để đi) trong khi bài toán JPDA chọn mục điểm dấu phù hợp nhất để gán với quỹ đạo. - Khi ứng dụng mạng nơron Hopfield vào giải hai bài toán, lôgic xây dựng ma trận cũng giống nhau: 12 + Ở TSP, các cột là thứ tự đến các thành phố, các hàng là đại diện cho các thành phố trong hành trình. + ở JPDA, các cột là các quỹ đạo đã khởi tạo của các mục tiêu, các hàng là các điểm dấu đo. - Các điều kiện ràng buộc cho từng bài toán cùng tƣơng tự: Điều kiện ràng buộc theo hàng ma trận: + Với TSP: Không thể cùng một lúc đến hai thành phố. + Với JPDA: Không thể ứng với một quỹ đạo mà lại có hai điểm dấu. Điều kiện ràng buộc theo cột ma trận: + Với TSP: Với mỗi thành phố chỉ đƣợc đến đúng một lần. + Với JPDA: Không thể với một điểm dấu mà lại có nguồn gốc từ hai mục tiêu. Điều kiện xét tất cả các sự kiện: tất cả các thành phố đều đƣợc xem xét (TSP) tƣơng ứng là tất cả các điểm dấu đều đƣợc xét (JPDA). Vì vậy, về nguyên tắc việc xây dựng hàm năng lƣợng E cho hai bài toán cũng tƣơng ứng nhƣ nhau (ngoại trừ một số hạng trong hàm năng lƣợng của JPDA có thêm một ràng buộc qui định tổng các xác suất liên kết của một quỹ đạo bằng 1 thỏa mãn phƣơng trình (1.36), trong hàm năng lƣợng ETSP không có ràng buộc này). Tóm lại, vì có nhiều điểm tƣơng đồng giữa hai bài toán nên phƣơng pháp giải cũng không có nhiều sự khác nhau. Trong mục trƣớc đã xem xét cách giải bài toán TSP sau đây sẽ áp dụng vào giải bài toán JPDA. 2.3.2 Quá trình áp dụng mạng Hopfield giải bài toán LKDĐ ra đa trong xử lý cấp 2 : Ở đây, việc xác định xác suất LKĐD 𝛽𝑥 𝑖 (𝑘) từ các hàm hợp lý cũng gần giống và tƣơng tự nhƣ giải bài toán TSP. Nếu quy ƣớc mức đầu ra của nơron trong mạng là xác suất LKĐD, thì có thể xây dựng mô hình mạng với chỉ số hàng là các điểm dấu đo đƣợc và chỉ số cột là các mục tiêu, đầu vào mạng là các hàm hợp lý và đầu ra là 13 các xác suất liên kết. Hàm năng lƣợng LKĐD có dạng phƣơng trình (2.15) Trong đó 𝜌𝑥 𝑖 (k) là hàm chuẩn hóa của tỉ số hợp lý 𝑝𝑥 𝑖 (k) . Sau khi biến đổi, sử dụng hàm tiếp hợp T, hàm năng lƣợng có dạng: 𝐸𝐷𝐴𝑃 ∗ = − 1 2 𝑇𝑥 ,𝑖 ,𝑦 ,𝑗 𝑗𝑖𝑦𝑥 × 𝑉𝑥 ,𝑦 × 𝑉𝑦 ,𝑗 − 𝑉𝑥 ,𝑦 𝑖𝑥 × 𝐼𝑥 ,𝑖 (2.24) Xác suất hậu nghiệm tìm đƣợc sau khi tối thiểu hóa hàm năng lƣợng với bốn điều kiện ràng buộc (không thể thu đƣợc hai điểm dấu đồng thời từ một mục tiêu và cũng không thể có một điểm dấu đồng thời là của hai mục tiêu, với mỗi kết quả đo chỉ có duy nhất một điểm dấu chân thực...). Các bƣớc còn lại tƣơng tự nhƣ cách giải bài toán TSP. Kết luận Chƣơng 2 Việc giải bài toán LKĐD ra đa sử dụng công cụ mạng Hopfield cũng đƣợc giải quyết tƣơng tự nhƣ bài toán TSP. Đặc biệt trong đó, việc tính toán, xác định xác suất liên kết điểm dấu có mở rộng sử dụng thêm một hệ số trong xây dựng hàm năng lƣợng (2.15) bằng việc sử dụng hàm hợp lý chuẩn hóa (2.16) và bốn điều kiện ràng buộc sẽ dẫn tới việc mạng sẽ ổn định khi hàm năng lƣợng đạt giá trị cực tiểu, khi đó các giá trị xác suất liến kết sẽ đƣợc lấy tại đầu ra của mạng. Việc lựa chọn hợp lý các hệ số M1 M4 sẽ quyết định thời gian hội tụ của mạng. CHƢƠNG 3 MÔ PHỎNG, TÍNH TOÁN KẾT QUẢ TRÊN PHẦN MỀM MATLAB 3.1 Đặt đầu bài tính toán mô phỏng và tiêu chí đánh giá: 3.1.1 Mô tả đầu bài tính toán mô phỏng: 1. Mô tả đầu bài: "Ứng dụng công cụ mạng Hopfield tính toán xác suất LKĐD dùng trong lọc, bám quỹ đạo trong xử lý cấp 2 tin tức ra đa với số 14 lượng mục tiêu Imax được xử lý trong điều kiện có nhiễu tác động. Tiến hành đánh giá chúng theo các tiêu chí lựa chọn". 2. Các dữ liệu đầu vào: - Số lƣợng quỹ đạo có thể thực hiện không vƣợt quá Imax. - Số các chu kỳ nhịp lấy tin là Kmax. - Trong từng chu kỳ nhịp lấy tin k và ứng với mỗi quỹ đạo, tồn tại không quá 1 điểm dấu chân thực và không quá số điểm dấu giả xác định . 3. Các kết quả đầu ra cần có: - Các quỹ đạo đƣợc lọc, bám thể hiện trên đồ thị từng quỹ đạo tƣơng ứng với số lƣợng mục tiêu khác nhau. - Kết quả sai số bám sát. - Tập thời gian xử lý của mỗi mục tiêu. 3.1.2 Xây dựng tiêu chí đánh giá: Theo [23],[49], chỉ tiêu chất lƣợng lọc, bám xác định theo: - Số lƣợng quỹ đạo đƣợc bám trên tổng số các quỹ đạo thực. - Sai số giữa quỹ đạo lọc, bám so với quỹ đạo thực. - Và khả năng đáp ứng thời gian thực quá trình bám quỹ đạo là tổng thời gian xử lý của các mục tiêu so sánh với thời gian quan sát của đài ra đa. 3.2. Tổng hợp các lƣu đồ thuật toán tính toán, mô phỏng: 3.2.1 Tổng hợp lưu đồ thuật toán tổng quát: (Hình 3.1) 3.2.2. Tổng hợp thuật toán tạo và xuất dữ liệu đầu vào: (Hình 3.2) 3.2.3. Tổng hợp thuật toán tính toán xác suất LKĐD sử dụng mạng Hopfield: Ở đây, ta thực hiện tổ chức mạng Hopfield theo dạng ma trận. Trong đó: chỉ số theo hàng chỉ thị vị trí của điểm dấu trong gói tin, chỉ số theo cột chỉ thị chỉ số của mục tiêu trong tập hợp các quỹ đạo hiện thời. Một điểm lƣu ý ở đây, chỉ số hàng thứ 0 là để chỉ thị vị trí 15 của điểm dấu ngoại suy. Tại mỗi nút mạng, giá trị đầu ra của mạng Vxi chính là giá trị xác suất liên kết của điểm dấu thứ x đối với quỹ Hình 3.1: Lƣu đồ thuật toán tổng quát đạo mục tiêu thứ i. Giá trị đầu ra của nơron này sẽ đƣợc đƣa đến đầu vào của các nơron khác trong mạng thông qua một trọng số tiếp hợp Tx,i,y,j. Tác động vào mỗi nơron còn có thành phần hệ số bias Ix,i (Hình 3.3). Bộ trọng số liên kết Tx,i,y,j và hệ số bias Ix,i đƣợc cập nhật theo (2.22) và (2.23). Trong quá trình mô phỏng cũng giả thiết rằng, các điểm dấu nhận đƣợc để đƣa vào LKĐD là kết quả sau quá trình xử lý sơ cấp nên mọi tín hiệu tạp nội bộ, và các dạng nhiễu tạp tích cực tác động vào máy thu coi nhƣ đã đƣợc loại trừ. Các điểm dấu giả đƣợc giả thiết là do sự vƣợt ngƣỡng ngẫu nhiên của mức tạp (do sự nhầm lẫn của bộ xử lý sơ cấp tín hiệu ra đa). Start T¹ o vµ xuÊt d÷ liÖu m« pháng ®Çu vµo 1: k Khëi t¹ o vÞ trÝ ban ®Çu cho c¸ c quü ®¹ o maxkk M¹ ng Hopfield tÝnh XS LK§ D XuÊt d÷ liÖu vÒ x¸ c suÊt liª n kÕt Läc Kalman 1: kk XuÊt d÷ liÖu quü ®¹ o End + - 16 3.3. Tổng hợp bộ số liệu đầu vào mô phỏng và lựa chọn các tham số mạng Hopfiel và mục tiêu: Hình 3.2: Lƣu đồ thuật toán tạo, xuất dữ liệu đầu vào Theo phân tích ở các mục trƣớc, cùng với việc tham khảo tham số kỹ thuật của các đài ra đa và máy bay trong thực tế, bộ số liệu đầu vào dùng cho tính toán, mô phỏng đƣợc tổng hợp và khởi tạo ban đầu tƣơng ứng trong các Bảng 3.1 và 3.2 Kết quả mô phỏng: (Từ Hình 3.4 đến Hình 3.13 trong luận án). Quan sát kết quả mô phỏng LKĐD, lọc bám bằng công cụ Start ;maxI;maxk maxG § Æt 1 2 maxkk 3 4 maxIi 5 1: kk 6 iJ k k max max ? 1 7 iii qsiii HBHBHB TaVV : : 8 9 )cos(]),1[(:),( )sin(]),1[(:),( iqsitruetrue iqsitruetrue HBTVikYikY HBTVikXikX 10 )1,1(),(:),( )1,1(),(:),( randnlikYikY randnlikXikX Yitruemeasure Xitruemeasure 1: ii + - + - - + 1: k 12 11 1: i maxkk 13 G¸n tËp ®iÓm dÊu 14 max;0: MM 15 maxIi 16 )(%: maxMrandm 17 mMM : 18 maxmax IGM 19 mim 20 migg : )1,1(),(:),( )1,1(),(:),( randnikYgkZ randnikXgkZ XimeasurenoiseY XimeasurenoiseX 21 1: mm ii 1: kk 22 23 Luu tËp d÷ liÖu t¹o gi¶ dï ng cho tÝnh to¸n 24 End 25 + - - - - + + + § Æt ];;;;[ max00 i iiii JHBVR max1: Ii 17 Hình 3.3: Tổ chức mạng Hopfield xác định xác suất LKĐD mạng nơron Hopfield, ta có những nhận xét nhƣ sau: Các quỹ đạo sau lọc bám (đƣờng màu đỏ) đều thể hiện đúng các quy luật chuyển động của mục tiêu nhƣ đầu bài (đƣờng màu xanh) và 100% số mục tiêu đƣợc bám quỹ đạo. Điều này khẳng định rằng sự đúng đắn của phƣơng pháp. Về sai số lọc bám, quỹ đạo đƣợc LKĐD bằng phƣơng pháp mạng nơron đều có sai số lọc bám (đồ thị Hình 3.10) nằm trong giới hạn cho phép (nhỏ hơn sai số của đài ra đa). Điều này thoả mãn tiêu chí thứ hai trong Mục 3.1.2 thể hiện chất lƣợng của các bộ lọc bám. Tại các thời điểm mục tiêu cơ động (thời điểm thay đổi hƣớng bay), sai số lọc bám có xu hƣớng tăng nhƣng vẫn trong giới hạn cho phép và ngay sau thời điểm có động lại trở về trạng thái ổn định. .. .. .. .. .. . . . . . . . . . . . . . . . . .. .. V1,1 V1,2 V1,j V1,i U1,1 U1,2 U1,i U1,j I1,1 I1,2 I1,j I1,i .. . . . . . . . . . . . . . . . . .. .. T mục tiêu chỉ số i,j (m (k )+ 1 ) đ iể m d ấ u c h ỉ s ố x ,y Hướng lan truyền V0,1 V2,1 Nơ ron 18 Các giá trị ƣớc lƣợng tốc độ của mục tiêu sau bộ lọc bám (thực chất là của các bộ lọc Kalman) khi đƣa đến đầu vào nó các điểm dấu đƣợc gán với quỹ đạo mục tiêu bằng phƣơng pháp mạng nơron đều thỏa mãn các điều kiện ban đầu (Hình 3.10, tốc độ trung bình của mục tiêu là 300m/s). Tại thời điểm cơ động, giá trị tốc độ cũng thay đổi. Trong quá trình mô phỏng có giả thiết các mục tiêu có quỹ đạo giao cắt nhau. Kết quả là sau lọc bám vẫn đảm bảo bám sát đầy đủ số lƣợng quỹ đạo ban đầu, điều này rất khó thực hiện khi áp dụng LKĐD theo thuật toán lân cận gần nhất (NNA). Quá trình mô phỏng lọc bám cũng tính đến việc cơ động của mục tiêu theo hƣớng bay khác nhau nhƣ trong thực tế tác chiến (các mục tiêu không chuyển động thẳng). Đầu ra các bộ lọc bám vẫn đảm bảo kết quả ở đầu ra. Về thời gian xử lý LKĐD, lọc bám (các Bảng 3.3 3.5), khi số lƣợng mục tiêu còn ít (dƣới 5 mục tiêu), thời gian xử lý của hai phƣơng pháp gần nhƣ bằng nhau nhƣng khi số lƣợng mục tiêu tăng lên thì đã có sự khác nhau rõ rệt. Đến 20 mục tiêu thì phƣơng pháp truyền thống đã không còn đảm bảo đƣợc nữa, trong khi đó mạng nơron vẫn đảm bảo có kết quả lọc bám ở đầu ra. Trong phƣơng pháp nơron, các mục tiêu đƣợc xử lý song song nên thời gian xử lý với mỗi mục tiêu là nhƣ nhau trong toàn bộ chu kỳ quan sát của đài ra đa. Với cấu hình máy tính không phải là cao(máy tính DESKTOP có cấu hình Pentium I 5 cores, tốc đô ̣ 3GHz, RAM 4GB), với kết quả lọc bám 20 mục tiêu nhƣ mô phỏng đã đủ để chứng minh cho tính khả thi của phƣơng pháp này. Nếu thực hiện trên công nghệ nhúng (FPGA), DSP thì tốc độ xử lý sẽ đƣợc nâng cao hơn nữa, kết quả là số lƣợng quỹ đạo đƣợc bám sát sẽ đƣợc nhiều hơn. 19 KẾT LUẬN VÀ KIẾN NGHỊ A. Kết quả của luận án: 1. Đã tổng hợp một cách hệ thống về lý thuyết bài toán xử lý cấp 2 tin tức ra đa từ các mô hình tổ chức hệ thống ra đa đến các thuật toán đã áp dụng trong quá trình xử lý. Thông qua việc nghiên cứu, phân tích các thuật toán LKĐD ứng với các không gian mô hình động học của mục tiêu kết hợp với các tính chất, kết quả của lọc Kalman đã khẳng định LKĐD và lọc, bám quỹ đạo là hai mặt của một vấn đề không thể tách rời trong quá trình xử lý cấp 2 tin tức ra đa và đặc biệt quan trọng trong môi trƣờng dày đặc mục tiêu và có nhiễu tác động vào quá trình đo đạc tham số mục tiêu của đài ra đa. Đã phân tích, làm rõ lý do thuật toán JPDA mặc dù mang tính tổng quát, phù hợp với tình huống bám nhiều mục tiêu có quỹ đạo giao cắt nhƣng việc áp dụng gặp khó khăn về dung lƣợng tính toán. 2. Đã nghiên cứu tổng hợp lý thuyết mạng nơron nhân tạo (ANN), các loại mạng cụ thể và các ứng dụng của chúng, đi sâu phân tích về mạng nơron Hopfield, định lý Lyapunov, hàm năng lƣợng(mục 2.2.2.1)và những tính toán cụ thể cho các mô hình mạng phát triển từ Hopfield thông qua các điều kiện ràng buộc tối ƣu ... áp dụng để giải bài toán kinh điển TSP từ đó hình thành cách giải bài toán LKĐD trong ra đa. Các nội dung này đƣợc trình bày cụ thể ở Chƣơng 2 của luận án. 3. Đã hình thành cách giải quyết một bài toán LKĐD ra đa thông qua việc phân tích bài toán tối ƣu có điều kiện “Ngƣời bán hàng du lịch - TSP” và đƣa ra phƣơng pháp giải bằng công cụ mạng nơron Hopfield với mô hình mạng (Hình 2.13) và việc sử dụng hàm năng lƣợng (2.10) cùng các điều kiện ràng buộc. Các bƣớc thực hiện giải bao gồm: xây dựng sơ đồ 20 mạng; xác định các trọng số trong mạng; thiết kế hàm kích hoạt cho đến thiết kế đầu vào và hệ các biểu thức tính toán đi kèm (2.10)....(2.14) đã cho phép xây dựng quy trình giải bài toán LKĐD bằng mạng Hopfield. 4. Đã đặt ra đầu bài với các thông số sát với thực tế của các đài ra đa, phƣơng tiện bay, tình huống nhiễu để thực hiện mô hình hóa, lập trình phần mềm mô phỏng tính toán, xử lý đƣa ra kết quả nhƣ thực tế xử lý trên đài ra đa và đánh giá các kết quả nghiên cứu đối với các nội dung trên theo các tiêu chí đánh giá nhƣ: số lƣợng quỹ đạo bám trên tổng số quỹ đạo thực ở các tình huống khác nhau, độ chính xác ƣớc lƣợng tham số quỹ đạo và chất lƣợng bám sát. Đã tiến hành tổng hợp lƣu đồ thuật toán mô phỏng tổng quát (Hình 3.1). Đã tính toán xác suất LKĐD sử dụng mạng Hopfield theo phƣơng pháp cực tiểu hóa hàm năng lƣợng đƣợc xây dựng theo phƣơng trình Lyapunov với bốn điều kiện biên (bốn điều kiện ràng buộc) (2.17) ÷ (2.20). Công cụ mô phỏng sử dụng phần mềm tiên tiến MATLAB cho phép xem xét trực quan, đánh giá chính xác các kết quả quá trình xử lý cấp 2 tin tức ra đa ứng dụng công cụ mạng nơron. Các kết quả mô phỏng đã chứng minh ƣu thế về mặt thời gian thực của công cụ mạng nơron. B. Những đóng góp mới của luận án: Luận án đã có những đóng góp nhƣ sau vào lĩnh vực nghiên cứu xử lý cấp 2 tin tức ra đa: 1. Đã nghiên cứu áp dụng một phƣơng pháp để LKĐD ra đa mà cụ thể là xây dựng một bộ lọc bám quỹ đạo mục tiêu ra đa với việc ứng dụng phần mềm MATLAB xây dựng bộ chƣơng trình phần mềm mô phỏng, tính toán xử lý LKĐD trong xử lý cấp 2 tin tức ra đa áp dụng thuật toán JPDA dùng công cụ mạng nơron Hopfield so sánh với phƣơng thức tính toán giải tích đơn th
File đính kèm:
 tom_tat_luan_an_ung_dung_mang_noron_nhan_tao_trong_xu_ly_cap.pdf
tom_tat_luan_an_ung_dung_mang_noron_nhan_tao_trong_xu_ly_cap.pdf

