Tóm tắt Luận án Ước lượng và đánh giá sinh khối và dự trữ carbon trên mặt đất đối với Rkx và Rtr để làm cơ sở cho việc quản lý rừng ở tỉnh Ninh Thuận

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
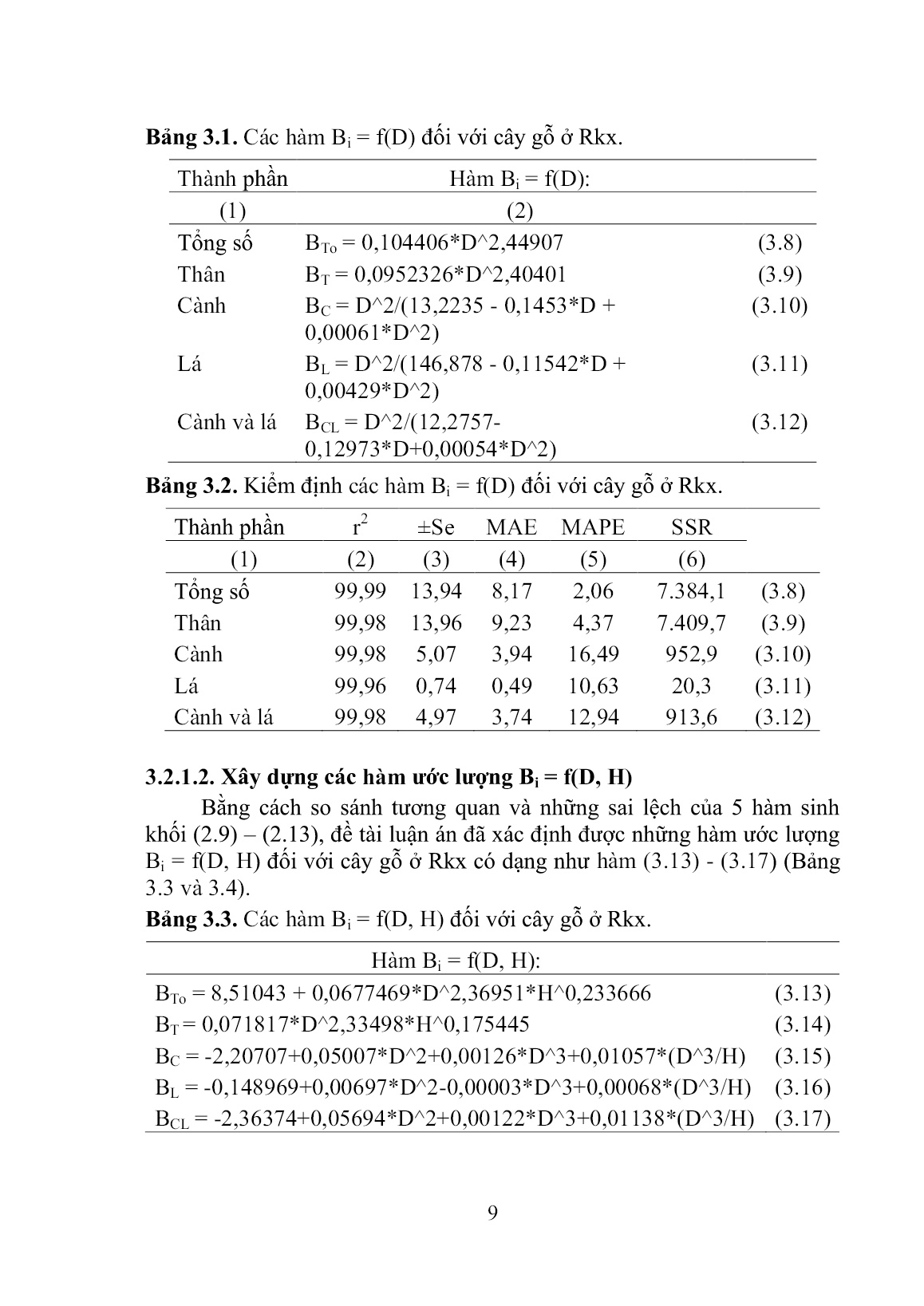
Trang 9
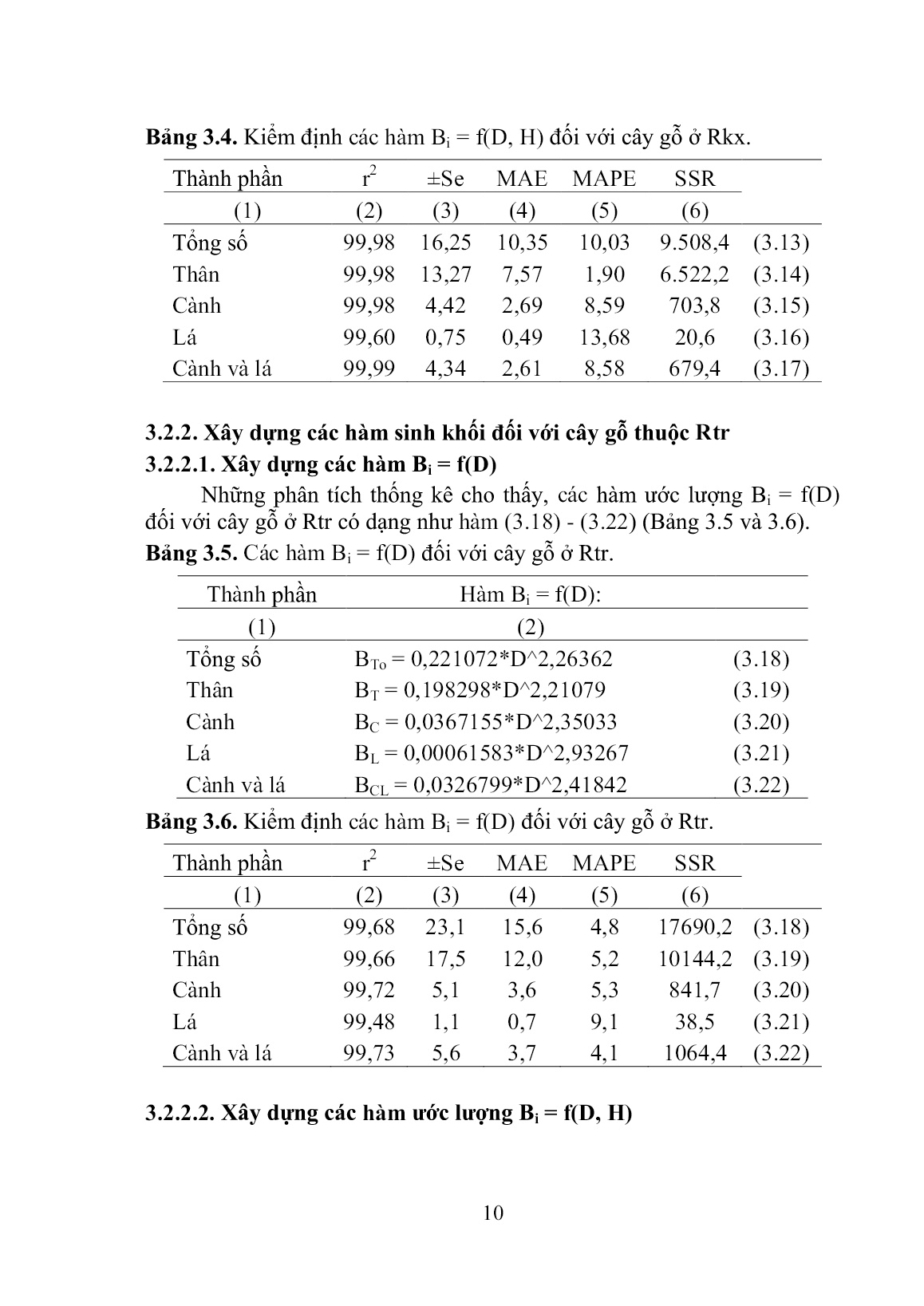
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Tóm tắt Luận án Ước lượng và đánh giá sinh khối và dự trữ carbon trên mặt đất đối với Rkx và Rtr để làm cơ sở cho việc quản lý rừng ở tỉnh Ninh Thuận", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Tóm tắt Luận án Ước lượng và đánh giá sinh khối và dự trữ carbon trên mặt đất đối với Rkx và Rtr để làm cơ sở cho việc quản lý rừng ở tỉnh Ninh Thuận

ử lý số liệu Nội dung 1. Phân tích tổ thành loài cây gỗ của Rkx và Rtr. Tổ thành quần thụ được xác định theo phương pháp của Thái Văn Trừng (1999). Cấu trúc của các trạng thái rừng được xác định thông qua phân bố N/D, phân bố N/H và phân bố M/D. Để dự đoán số cây theo cấp D, đề tài kiểm định hàm phân bố N/D ở các trạng thái rừng theo hàm phân bố mũ và phân bố lognormal. Nội dung 2. Xây dựng những hàm sinh khối đối với cây cá thể. Hàm ước lượng H = f(D) và V = f(D, H) được xây dựng dựa theo 3 hàm (2.1) – (2.3). H = 1/(a + b/D) (2.1) H = a*D^b (2.2) VT = a*D^b*H^c (2.3) Những hàm sinh khối đối với các thành phần (Bi = BT, BC, BL và BCL) được xác định theo hai dạng: Bi = f(D) và Bi = f(D, H). Những hàm Bi = f(D) được kiểm định theo 5 hàm (2.4) – (2.8). Những hàm thích hợp được chọn theo tiêu chuẩn SSRmin. Bi = a*exp(-b*D^-c) (2.4) Bi = D^2/(a+b*D + c*D^2) (2.5) Bi = a*D^b (2.6) Bi = a*(1-exp(-b*D))^c (2.7) B = a*exp(b*D) (2.8) Những hàm ước lượng Bi = f(D, H) được kiểm định theo 5 hàm (2.9 – 2.13). Những hàm thích hợp được chọn theo tiêu chuẩn SSRmin. B = a*D^b*H^c (2.9) B = a + b*D^2 + c*D^3 + d*(D^3/H) (2.10) B = a + b*D^2 + c*(D^2/H) (2.11) B = a*(D^2*H)^b (2.12) B = a*(D*H)^b (2.13) Nội dung 3. Phương pháp ước lượng sinh khối dựa theo số liệu điều tra rừng. Ở đây Bi được xác định theo 5 phương pháp. Phương pháp 1 xác định sinh khối quần thụ dựa theo số liệu của những ô mẫu kết hợp với hàm B = f(D). Phương pháp 2 xác định sinh khối cây gỗ dựa theo thể tích thân cây gỗ. Hàm Bi = f(V) thích hợp được kiểm định theo 2 hàm (2.14) và (2.15). Phương pháp 3 xác định sinh khối cây gỗ dựa theo hệ số điều 7 chỉnh sinh khối: Bi = VThân*BEFi. Hàm BEFi = f(X) (X = D và V) thích hợp được kiểm định theo 3 hàm (2.16) và (2.18). Bi = a*V^b (2.14) Bi = V^2/(a + b*V - c*V^2) (2.15) BEFi = (a + b/X)^2 (2.16) BEFi = a*X^b (2.17) BEFi = sqrt(a + b/X) (2.18) Phương pháp 4 xác định sinh khối cây cá thể dựa theo tỷ lệ sinh khối của các thành phần: Bi = BThân*Ri. Hàm Ri = f(D) thích hợp được kiểm định theo 3 hàm (2.19) và (2.21). Ri = a + b*ln(D) (2.19) Ri = 1/(a + b*sqrt(D)) (2.20) Ri = a*D^b (2.21) Phương pháp 5 xác định sinh khối quần thụ dựa theo hàm Bi = f(G) và Bi = f(M). Hàm Bi = f(X) (X = G và M) thích hợp được kiểm định theo 3 hàm (2.22) và (2.24). Bi = sqrt(a + b*X^2 (2.22) Bi = a*X^b (2.23) Bi = X^2/(a + b*X + c*X^2) (2.24) Nội dung 4. So sánh những phương pháp xác định sinh khối. Trong đề tài này, sinh khối ở mức cây gỗ đã được ước lượng theo 6 phương pháp khác nhau: Bi = f(D); Bi = f(D, H); Bi = f(V); Bi = V*BEFi với BEFi = f(D); Bi = V*BEFi với BEFi = f(V); Bi = BT*Ri với Ri = f(D). Sinh khối quần thụ được xác định theo 4 phương pháp: Sử dụng hàm sinh khối cây cá thể và số liệu điều tra trên những ô mẫu; Bi = f(G); Bi = f(M); Hàm phân bố N/D cùng với những hàm Bi = f(D). Sự khác biệt giữa các phương pháp ước lượng sinh khối cây gỗ và quần thụ được so sánh bằng bảng ANOVA. Nội dung 5. Ước lượng sinh khối và dự trữ C của Rkx và Rtr. Sinh khối bình quân trên 1 ha được xác định bằng các hàm sinh khối kết hợp với số liệu của các ô mẫu. Khối lượng các bon (C, tấn) dự trữ trong sinh khối trên mặt đất đối với Rkx và Rtr được xác định bằng cách nhân diện tích rừng với sinh khối 1 ha; trong đó PC = 0,47. Khối lượng CO2 (tấn) mà hai kiểu đã hấp thu được xác định bằng cách nhân khối lượng C (tấn/ha) với hệ số chuyển đổi từ CO2 thành C. 8 Chƣơng 3 KẾT QUẢ NGHIÊN CỨU VÀ THẢO LUẬN 3.1. Kết cấu loài cây gỗ và cấu trúc của Rkx và Rtr 3.1.1. Kết cấu loài cây gỗ và cấu trúc của Rkx Kết quả nghiên cứu cho thấy, số loài cây gỗ bắt gặp là 39 loài. Mật độ dao động từ 212 – 483 cây/ha; trung bình 374 cây/ha. Tiết diện ngang dao động từ 7,7 – 22,3 m2/ha; trung bình 13,6 m2/ha. Trữ lượng gỗ dao động từ 51,4 - 190,0 m3/ha; trung bình 104,0 m3/ha. Phân bố N/D của trạng thái rừng IIB có dạng 1 đỉnh lệch trái và phù hợp với phân bố lognormal (3.1). Phân bố N/D của trạng thái rừng IIIA1, IIIA2 và IIIA3 có dạng giảm theo hình chữ “J” và phù hợp với hàm phân bố mũ (3.2 – 3.4). f(x) = (1/Di*4,24 2 )*exp(-ln(Di- 15,7) 2 /2*4,24 2 ) (3.1) N = 120,634*exp(-0,04342*D) - 12,1688 (3.2) N = 326,199*exp(-0,07162*D) – 4,40842 (3.3) N = 486,372*exp(-0,10759*D) + 6,53792 (3.4) Phân bố N/H của trạng thái rừng IIB có dạng một đỉnh, còn trạng thái rừng IIIA1 – IIIA3 có dạng nhiều đỉnh. 3.1.2. Kết cấu loài cây gỗ và cấu trúc của Rtr Kết quả nghiên cứu cho thấy, số loài cây gỗ bắt gặp là 25 loài. Mật độ dao động từ 211 – 414 cây/ha; trung bình 297 cây/ha. Tiết diện ngang từ 5,5 – 14,0 m2/ha; trung bình 8,8 m2/ha. Trữ lượng gỗ từ 48,0 - 99,2 m 3 /ha; trung bình 64,4 m 3/ha. Phân bố N/D của 3 trạng thái rừng IIB, IIIA1 và IIIA2 có dạng giảm theo hình chữ “J” và phù hợp với hàm phân bố mũ (3.5 – 3.7). Đường cong phân bố N/H của cả 3 trạng thái rừng này đều có dạng nhiều đỉnh. N = 172,106*exp(-0,085892*D) + 0,788579 (3.5) N = 154,023*exp(-0,086861*D) – 0,722805 (3.6) N = 241,783*exp(-0,068680*D) – 7,16333 (3.7) 3.2. Xây dựng các hàm sinh khối đối với cây gỗ thuộc Rkx và Rtr 3.2.1. Xây dựng các hàm sinh khối đối với cây gỗ thuộc Rkx 3.2.1.1. Xây dựng các hàm Bi = f(D) Bằng cách so sánh tương quan và sai lệch của 5 hàm sinh khối (2.4) – (2.8), đề tài luận án đã xác định được những hàm ước lượng Bi = f(D) đối với cây gỗ ở Rkx có dạng như hàm (3.8) - (3.12) (Bảng 3.1 và 3.2). 9 Bảng 3.1. Các hàm Bi = f(D) đối với cây gỗ ở Rkx. Thành phần Hàm Bi = f(D): (1) (2) Tổng số BTo = 0,104406*D^2,44907 (3.8) Thân BT = 0,0952326*D^2,40401 (3.9) Cành BC = D^2/(13,2235 - 0,1453*D + 0,00061*D^2) (3.10) Lá BL = D^2/(146,878 - 0,11542*D + 0,00429*D^2) (3.11) Cành và lá BCL = D^2/(12,2757- 0,12973*D+0,00054*D^2) (3.12) Bảng 3.2. Kiểm định các hàm Bi = f(D) đối với cây gỗ ở Rkx. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 99,99 13,94 8,17 2,06 7.384,1 (3.8) Thân 99,98 13,96 9,23 4,37 7.409,7 (3.9) Cành 99,98 5,07 3,94 16,49 952,9 (3.10) Lá 99,96 0,74 0,49 10,63 20,3 (3.11) Cành và lá 99,98 4,97 3,74 12,94 913,6 (3.12) 3.2.1.2. Xây dựng các hàm ƣớc lƣợng Bi = f(D, H) Bằng cách so sánh tương quan và những sai lệch của 5 hàm sinh khối (2.9) – (2.13), đề tài luận án đã xác định được những hàm ước lượng Bi = f(D, H) đối với cây gỗ ở Rkx có dạng như hàm (3.13) - (3.17) (Bảng 3.3 và 3.4). Bảng 3.3. Các hàm Bi = f(D, H) đối với cây gỗ ở Rkx. Hàm Bi = f(D, H): BTo = 8,51043 + 0,0677469*D^2,36951*H^0,233666 (3.13) BT = 0,071817*D^2,33498*H^0,175445 (3.14) BC = -2,20707+0,05007*D^2+0,00126*D^3+0,01057*(D^3/H) (3.15) BL = -0,148969+0,00697*D^2-0,00003*D^3+0,00068*(D^3/H) (3.16) BCL = -2,36374+0,05694*D^2+0,00122*D^3+0,01138*(D^3/H) (3.17) 10 Bảng 3.4. Kiểm định các hàm Bi = f(D, H) đối với cây gỗ ở Rkx. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 99,98 16,25 10,35 10,03 9.508,4 (3.13) Thân 99,98 13,27 7,57 1,90 6.522,2 (3.14) Cành 99,98 4,42 2,69 8,59 703,8 (3.15) Lá 99,60 0,75 0,49 13,68 20,6 (3.16) Cành và lá 99,99 4,34 2,61 8,58 679,4 (3.17) 3.2.2. Xây dựng các hàm sinh khối đối với cây gỗ thuộc Rtr 3.2.2.1. Xây dựng các hàm Bi = f(D) Những phân tích thống kê cho thấy, các hàm ước lượng Bi = f(D) đối với cây gỗ ở Rtr có dạng như hàm (3.18) - (3.22) (Bảng 3.5 và 3.6). Bảng 3.5. Các hàm Bi = f(D) đối với cây gỗ ở Rtr. Thành phần Hàm Bi = f(D): (1) (2) Tổng số BTo = 0,221072*D^2,26362 (3.18) Thân BT = 0,198298*D^2,21079 (3.19) Cành BC = 0,0367155*D^2,35033 (3.20) Lá BL = 0,00061583*D^2,93267 (3.21) Cành và lá BCL = 0,0326799*D^2,41842 (3.22) Bảng 3.6. Kiểm định các hàm Bi = f(D) đối với cây gỗ ở Rtr. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 99,68 23,1 15,6 4,8 17690,2 (3.18) Thân 99,66 17,5 12,0 5,2 10144,2 (3.19) Cành 99,72 5,1 3,6 5,3 841,7 (3.20) Lá 99,48 1,1 0,7 9,1 38,5 (3.21) Cành và lá 99,73 5,6 3,7 4,1 1064,4 (3.22) 3.2.2.2. Xây dựng các hàm ƣớc lƣợng Bi = f(D, H) 11 Những phân tích thống kê cho thấy, các hàm ước lượng B = f(D, H) đối với cây gỗ ở Rtr có dạng như hàm (3.23) - (3.27) (Bảng 3.7 và 3.8). Bảng 3.7. Các hàm Bi = f(D, H) đối với cây gỗ ở Rtr. Hàm Bi = f(D, H): BTo = -36,6254+1,63824*D^2+0,01484*D^3- 0,90699*(D^3/H) (3.23) BT = -28,1845+1,2815*D^2+0,010773*D^3- 0,705187*(D^3/H) (3.24) BC = 0,0109769*D^0,454818*H^2,64175 (3.25) BL = -1,46167+0,08332*D^2+0,001258*D^3- 0,06336*(D^3/H) (3.26) BCL = 0,0072315*D^0,047762*H^3,30274 (3.27) Bảng 3.8. Kiểm định các hàm Bi = f(D, H) đối với cây gỗ ở Rtr. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 99,70 23,2 16,3 6,7 16.644,3 (3.18) Thân 99,68 17,5 12,3 6,6 9493.9 (3.19) Cành 99,73 5,0 3,5 5,3 797.0 (3.20) Lá 99,53 1,1 0,7 14,9 34,3 (3.21) Cành và lá 99,75 5,5 3,7 4,1 982,8 (3.22) 3.2.3. Xây dựng các hàm sinh khối trên mặt đất từ số liệu điều tra Rkx 3.2.3.1. Hàm sinh khối dựa theo thể tích thân cây (1) Hàm thể tích thân cây Những phân tích thống kê cho thấy, hàm ước lượng H = f(D) có dạng như hàm (3.28). Hàm ước lượng V = f(D, H) có dạng như hàm (3.29). Các hàm ước lượng Bi = f(V) có dạng như hàm 3.30 - 3.34 (Bảng 3.9 – 3.10). H = 1/(0,0244541 + 0,984367/D) (3.28) r 2 = 99,4%; Se = 0,003; P < 0,001. V = 0,0000349*D^1,99334*H^1,01211 (3.29) R 2 = 99,9%; Se = 0,003; P < 0,001. 12 (2) Hàm ƣớc lƣợng sinh khối dựa theo thể tích thân cây Các hàm ước lượng Bi = f(V) đối với cây gỗ ở Rkx có dạng như hàm (3.30) - (3.34) (Bảng 3.9 và 3.10). Bảng 3.9. Các hàm Bi = f(V) đối với cây gỗ ở Rkx. Thành phần Hàm Bi = f(V): (1) (2) Tổng số BTo = V^2/(-0,000033+0,001361*V- 0,000011*V^2) (3.30) Thân BT = 581,374*V^1,00316 (3.31) Cành BC = V^2/(-0,000078+0,006204*V- 0,000139*V^2) (3.32) Lá BL = 9,69685*V^0,761433 (3.33) Cành và lá BCL = V^2/(-0,000140+0,005939*V- 0,000123*V^2) (3.34) Bảng 3.10. Kiểm định hàm Bi = f(V) đối với cây gỗ ở Rkx. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 99,98 16,40 11,18 18,60 9.953,1 (3.30) Thân 99,98 16,85 12,78 7,49 10.797,1 (3.31) Cành 99,98 5,33 3,25 35,05 1.054,7 (3.32) Lá 99,59 0,73 0,49 11,43 20,7 (3.33) Cành và lá 99,98 4,92 3,14 19,42 895,6 (3.34) 3.2.3.2. Xây dựng các hàm điều chỉnh sinh khối đối với cây gỗ thuộc Rkx (1) Hàm ƣớc lƣợng BEFi = f(D) Những phân tích thống kê cho thấy, các hàm ước lượng BEFi = f(D) đối với cây gỗ ở Rkx có dạng như hàm (3.35) – (3.38) (Bảng 3.11 – 3.12). Bảng 3.11. Các hàm BEFi = f(D) đối với cây gỗ thuộc Rkx. Thành phần Hàm BEFi = f(D) đối với các thành phần: (1) (2) Tổng số BEFTo = (0,835973 + 1,65451/D)^2 (3.35) 13 Thân BEFT = (0,726805 + 1,786060/D)^2 (3.36) Cành BEFC = (0,370148 + 1,695580/D)^2 (3.37) Cành và lá BEFCL = (0,380201 + 1,75667/D)^2 (3.38) Bảng 3.12. Kiểm định sai lệch của các hàm BEFi = f(D) đối với cây gỗ thuộc Rkx. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 98,19 0,0181 0,0137 1,67 0,0125 (3.35) Thân 99,36 0,0104 0,0082 1,26 0,0042 (3.36) Cành 96,36 0,0140 0,0104 5,42 0,0075 (3.37) Cành và lá 97,16 0,0132 0,0097 4,84 0,0066 (3.38) Bằng cách thay thế D vào các hàm (3.35) – (3.38) ở Bảng 3.11, có thể nhận thấy các hệ số BEFi đều giảm dần theo sự gia tăng cấp D (cm); trong đó BEFi ở cấp D = 10 - 46 cm suy giảm nhanh hơn so với cấp D = 46 – 94 cm. Nói chung, khi dự đoán BEFi (tấn/m 3) dựa theo cấp D = 10 - 94 cm, thì các hệ số BEFTo, BEFT, BEFC và BEFCL bình quân tương ứng là 0,783; 0,608; 0,177 và 0,187 (tấn/m3). (2) Hàm ƣớc lƣợng BEFi = f(V) Những phân tích thống kê cho thấy, các hàm ước lượng BEFi = f(V) đối với cây gỗ ở Rkx có dạng như hàm (3.39) – (3.42) (Bảng 3.13 – 3.14). Bảng 3.13. Các hàm ước lượng BEFi = f(V) đối với cây gỗ thuộc Rkx. Thành phần Hàm BEFi = f(V) đối với các thành phần: (1) (2) Tổng số BEFTo = sqrt(0,618877 + 0,006341/V) (3.39) Thân BEFT = sqrt(0,372672 + 0,005066/V) (3.40) Cành BEFC = sqrt(0,030549 + 0,001097/V) (3.41) Cành và lá BEFCL = sqrt(0,034115 + 0,001237/V) (3.42) 14 Bảng 3.14. Kiểm định sai lệch của các hàm BEFi = f(V) đối với cây gỗ thuộc Rkx. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 89,80 0,0430 0,0327 3,70 0,0703 (3.39) Thân 89,53 0,0422 0,0337 4,91 0,0678 (3.40) Cành 96,41 0,0139 0,0110 5,20 0,0074 (3.41) Cành và lá 95,76 0,0161 0,0125 5,48 0,0099 (3.42) Bằng cách thay thế V vào các hàm (3.39) – (3.42) ở Bảng 3.13, có thể nhận thấy các giá trị BEFi đều giảm dần theo sự gia tăng V; trong đó BEFi ở cấp V < 0,4652 (tương ứng cấp D < 28 cm) giảm nhanh hơn so với cấp V = 0,4652 – 8,9113 (tương ứng cấp D = 28 – 94 cm). Nói chung, khi dự đoán BEFi (tấn/m 3) dựa theo V (m3) tương ứng với cấp D = 10 – 94 cm, thì BEFTo, BEFT, BEFC và BEFCL bình quân tương ứng là 0,801; 0,625; 0,185 và 0,195 (tấn/m3). (3) Hàm ƣớc lƣợng tỷ lệ sinh khối đối với cây gỗ ở Rkx Những phân tích thống kê cho thấy, hàm ước lượng Ri = f(D) đối với cây gỗ ở Rkx có dạng như hàm (3.43) – (3.46) (Bảng 3.15 – 3.16). Nói chung, tốc độ gia tăng RTo và RCL ở cấp D = 10 – 46 cm nhanh hơn so với cấp D = 46 – 94 cm. So với sinh khối thân cây thuộc cấp D = 10 – 94 cm (100%), các giá trị RTo, RC, RL và RCL bình quân tương ứng là 130,0%, 28,5%, 1,5% và 30,0%. Bảng 3.15. Các hàm ước lượng Ri = f(D) đối với những cây gỗ ở Rkx. Thành phần Hàm Ri = f(D) đối với các thành phần: (1) (2) Tổng số RTo = 1,08383 + 0,05718*Ln(D) (3.43) Cành RC = 0,0345055 + 0,0662483*Ln(D) (3.44) Lá RL = 1/(6,17273 + 9,12935*sqrt(D)) (3.45) Cành và lá RCL = 0,08383 + 0,05718*Ln(D) (3.46) 15 Bảng 3.16. Kiểm định sai lệch của các hàm Ri = f(D) đối với những cây gỗ ở Rkx. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 99,58 0,0026 0,0012 0,74 0,0004 (3.43) Cành 99,40 0,0036 0,0012 0,74 0,0005 (3.44) Lá 96,62 0,0012 0,0005 2,40 0,0001 (3.45) Cành và lá 99,58 0,0026 0,0012 0,55 0,0002 (3.46) 3.2.3.3. Xây dựng hàm sinh khối đối với quần thụ thuộc Rkx (1) Hàm ƣớc lƣợng Bi = f(G) Những phân tích thống kê cho thấy, hàm ước lượng Bi = f(G) đối với Rkx có dạng như hàm (3.47) – (3.49) (Bảng 3.17 – 3.18). Bảng 3.17. Các hàm Bi = f(G) đối với Rkx. Thành phần Hàm Bi = f(G) đối với các thành phần: (1) (2) Tổng số BTo = G^2/(-0,00541+0,17501*G - 0,00088*G^2) (3.47) Thân BT = G^2/(-0,06271 + 0,22824*G - 0,00114*G^2) (3.48) Cành và lá BCL = G^2/(-0,10538 + 0,71008*G - 0,00294*G^2) (3.49) Bảng 3.18. Kiểm định các hàm Bi = f(G) đối với Rkx. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 97,6 11,1 8,6 11,1 2.103,8 (3.47) Thân 97,9 7,9 6,2 10,3 1.072,5 (3.48) Cành và lá 97,4 2,7 2,1 10,3 126,8 (3.49) (2) Hàm ƣớc lƣợng Bi = f(M) Hàm ước lượng Bi = f(M) đối với Rkx có dạng như hàm (3.50) – (3.52) (Bảng 3.19 – 3.20). 16 Bảng 3.19. Các hàm Bi = f(M) đối với Rkx. Thành phần Hàm Bi = f(M) đối với các thành phần: (1) (2) Tổng số BTo = M^2/(9,55951 + 1,00007*M + 0,00109*M^2) (3.50) Thân BT = M^2/(9,67883 + 1,301610*M + 0,00142*M^2) (3.51) Cành và lá BCL = M^2/(32,4375 + 4,08979*M + 0,00492*M^2) (3.52) Bảng 3.20. Kiểm định các hàm Bi = f(M) đối với Rkx. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 98,4 9,2 6,4 8,3 1.436,2 (3.50) Thân 98,6 6,5 4,5 7,6 730,0 (3.51) Cành và lá 98,2 2,2 1,5 7,5 91,7 (3.52) 3.2.4. Xây dựng các hàm sinh khối trên mặt đất từ số liệu điều tra Rtr 3.2.4.1. Hàm sinh khối dựa theo thể tích thân cây (1) Hàm thể tích thân cây Những phân tích thống kê cho thấy, hàm ước lượng H = f(D) có dạng như hàm (3.53). Hàm ước lượng V = f(D, H) có dạng như hàm (3.54). Hàm ước lượng Bi = f(V) có dạng như hàm 3.55 – 3.59 (Bảng 3.21 – 3.22). H = 1,58532*D^0,716512 (3.53) r 2 = 94,7%; Se = 1,3; MAE = 1,1; MAPE = 9,7%; P < 0,001. V = 0,000035*D^1,99997*H^1,00003 (3.54) R 2 = 99,9%; Se = 0,00003; MAE = 00002; MAPE = 0,02%. (2) Hàm ƣớc lƣợng sinh khối dựa theo thể tích thân cây Các hàm ước lượng Bi = f(V) đối với cây gỗ ở Rtr có dạng như hàm (3.55) - (3.59) (Bảng 3.21 và 3.22). 17 Bảng 3.21. Các hàm Bi = f(V) đối với cây gỗ ở Rtr. Thành phần Hàm Bi = f(V): (1) (2) Tổng số BTo = 777,839*V^0,83301 (3.55) Thân BT = 576,648*V^0,81357 (3.56) Cành BC = 176,646*V^0,86493 (3.57) Lá BL = 24,1928*V^1,08280 (3.58) Cành và lá BCL = 201,023*V^0,89003 (3.59) Bảng 3.22. Kiểm định các hàm Bi = f(V) đối với cây gỗ ở Rtr. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 99,68 22,9 15,5 4,8 17.289,6 (3.55) Thân 99,66 17,3 11,9 5,3 9.926,6 (3.56) Cành 99,72 5,0 3,6 5,3 825,2 (3.57) Lá 99,49 1,1 0,9 9,2 37,2 (3.58) Cành và lá 99,74 5,5 3,7 4,1 1036,7 (3.59) 3.2.4.2. Xây dựng các hàm điều chỉnh sinh khối đối với cây gỗ thuộc Rtr (1) Hàm ƣớc lƣợng BEFi = f(D) Những phân tích thống kê cho thấy, hàm ước lượng BEFi = f(D) đối với cây gỗ ở Rtr có dạng như hàm (3.60) – (3.63) (Bảng 3.23 – 3.24). Bảng 3.23. Các hàm BEFi = f(D) đối với cây gỗ thuộc Rtr. Thành phần Hàm BEFi = f(D) đối với các thành phần: (1) (2) Tổng số BEFTo = 3,98667*D^-0,452887 (3.60) Thân BEFT = 3,5747*D^-0,505579 (3.61) Cành BEFC = 0,662015*D^-0,365971 (3.62) Cành và lá BEFCL = 0,588873*D^-0,297814 (3.63) 18 Bảng 3.24. Kiểm định sai lệch của các hàm BEFi = f(D) đối với cây gỗ thuộc Rtr. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 99,98 0,0030 0,0020 0,18 0,00030 (3.60) Thân 99,98 0,0020 0,0010 0,19 0,00020 (3.61) Cành 99,97 0,0007 0,0005 0,22 0,00002 (3.62) Cành và lá 99,97 0,0007 0,0004 0,18 0,00001 (3.63) Bằng cách thay thế D vào các hàm (3.60) – (3.63) ở Bảng 3.23, có thể nhận thấy BEFi của những thành phần cây gỗ ở Rtr đều giảm dần từ cấp D = 8 - 48 cm; trong đó BEFi ở cấp D < 28 cm giảm nhanh hơn so với cấp D = 28 – 48 cm. Nói chung, các hệ số BEFTo, BEFT, BEFC và BEFCL bình quân của các cây gỗ ở cấp D = 8 - 48 cm tương ứng là 0,965; 0,737; 0,209 và 0,230 (tấn/m3). (2) Hàm ƣớc lƣợng BEFi = f(V) Những phân tích thống kê cho thấy, hàm ước lượng BEFi = f(V) đối với cây gỗ ở Rtr có dạng như hàm (3.64) – (3.67) (Bảng 3.25 – 3.26). Bảng 3.25. Các hàm BEFi = f(V) đối với cây gỗ thuộc Rtr. Thành phần Hàm BEFi = f(V) đối với các thành phần: (1) (2) Tổng số BEFTo = 0,778104*V^-0,166735 (3.64) Thân BEFT = 0,576873*V^-0,186159 (3.65) Cành BEFC = 0,176799*V^-0,134731 (3.66) Cành và lá BEFCL = 0,201092*V^-0,109643 (3.67) Bảng 3.26. Kiểm định sai lệch của các hàm BEFi = f(V) đối với cây gỗ thuộc Rtr. Thành phần r2 ±Se MAE MAPE SSR (1) (2) (3) (4) (5) (6) Tổng số 99,98 0,002 0,001 0,15 0,00023 (3.64) Thân 99,99 0,002 0,001 0,16 0,00015 (3.65) Cành 99,97 0,007 0,005 0,20 0,00014 (3.66) Cành và lá 99,97 0,006 0,004 0,17 0,00001 (3.67) 19 Bằng cách thay thế V vào các hàm (3.64) – (3.67) ở Bảng 3.25, có thể nhận thấy các hệ số BEFi đều giảm dần theo sự gia tăng V; trong đó BEFi giảm nhanh ở cấp V < 0,473 m 3 (tương ứng D < 28 cm), giảm chậm ở cấp V = 0,473 – 2,048 m3 (tương ứng D = 28 – 48 cm). Nói chung, các hệ số BEFTo, BEFT, BEFC và BEFCL bình quân đối với cây gỗ ở cấp V = 0,016 m 3 – 2,048 m3 (tương ứng 8 cm < D < 48 cm) tương ứng là 0,965; 0,737; 0,209 và 0,230 (tấn/m3). (3) Hàm ƣớc lƣợng tỷ lệ sinh khối đối với cây gỗ ở Rtr Những phân tích thống kê cho thấy, hàm ước lượng Ri = f(D) đối với cây gỗ ở Rtr có dạng như hàm (3.68) – (3.71) (Bảng 3.27 – 3.28). Bảng 3.27. Các hàm ước lượng Ri = f(D) đối với những cây gỗ ở Rtr. Thành phần Hàm Ri = f(D) đối với các thành phần: (1) (2) Tổng số RTo = 1,12951*D^0,0490917 (3.68) Cành RC = 0,184868*D^0,139972 (3.69) Lá RL = 0,00317027*D^0,716111 (3.70) Cành và lá RCL = 0,164518*D^0,208156 (3.71) Bảng 3.28. Kiểm định sai lệch của hàm Ri = f(D) đ
File đính kèm:
 tom_tat_luan_an_uoc_luong_va_danh_gia_sinh_khoi_va_du_tru_ca.pdf
tom_tat_luan_an_uoc_luong_va_danh_gia_sinh_khoi_va_du_tru_ca.pdf

