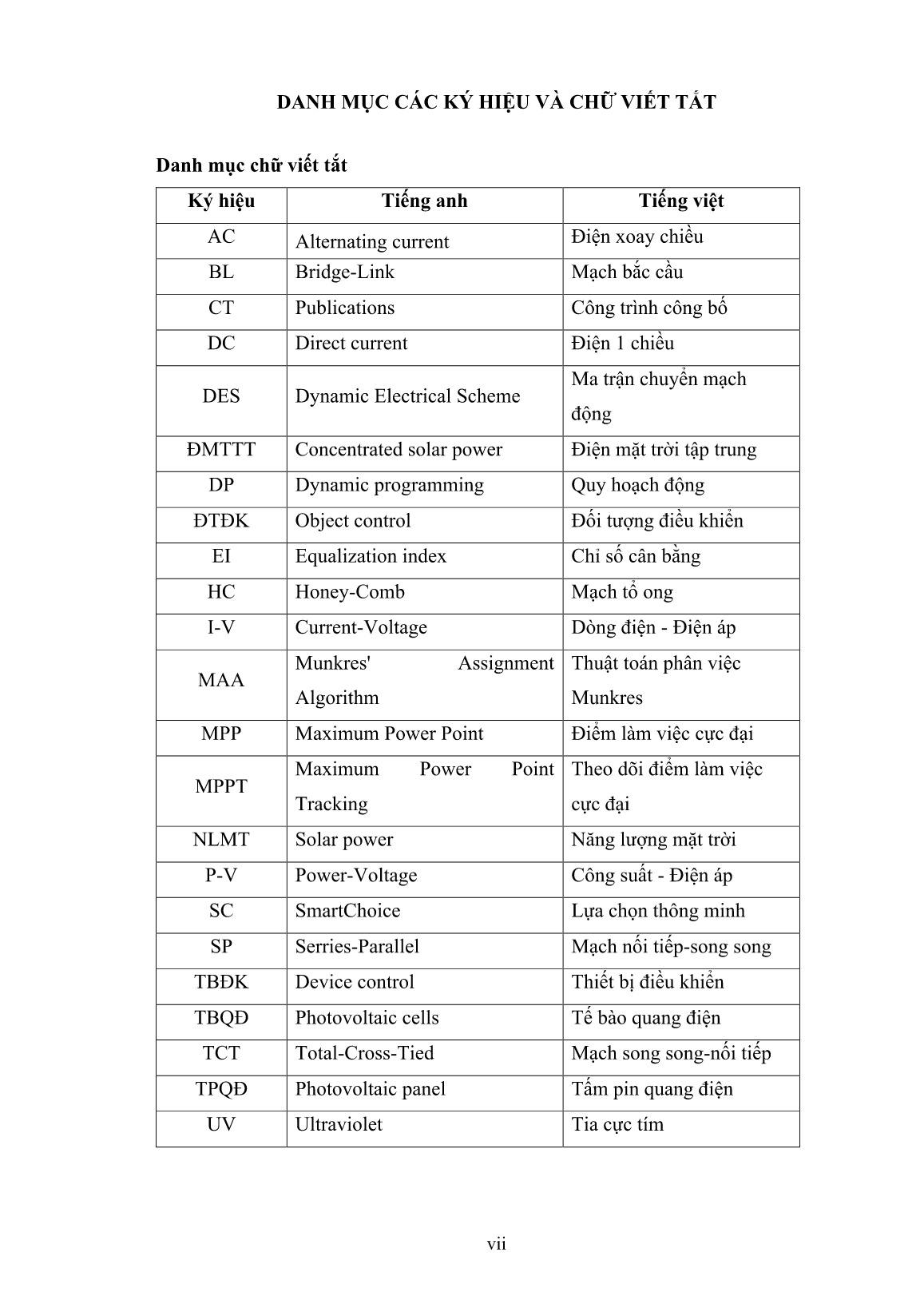
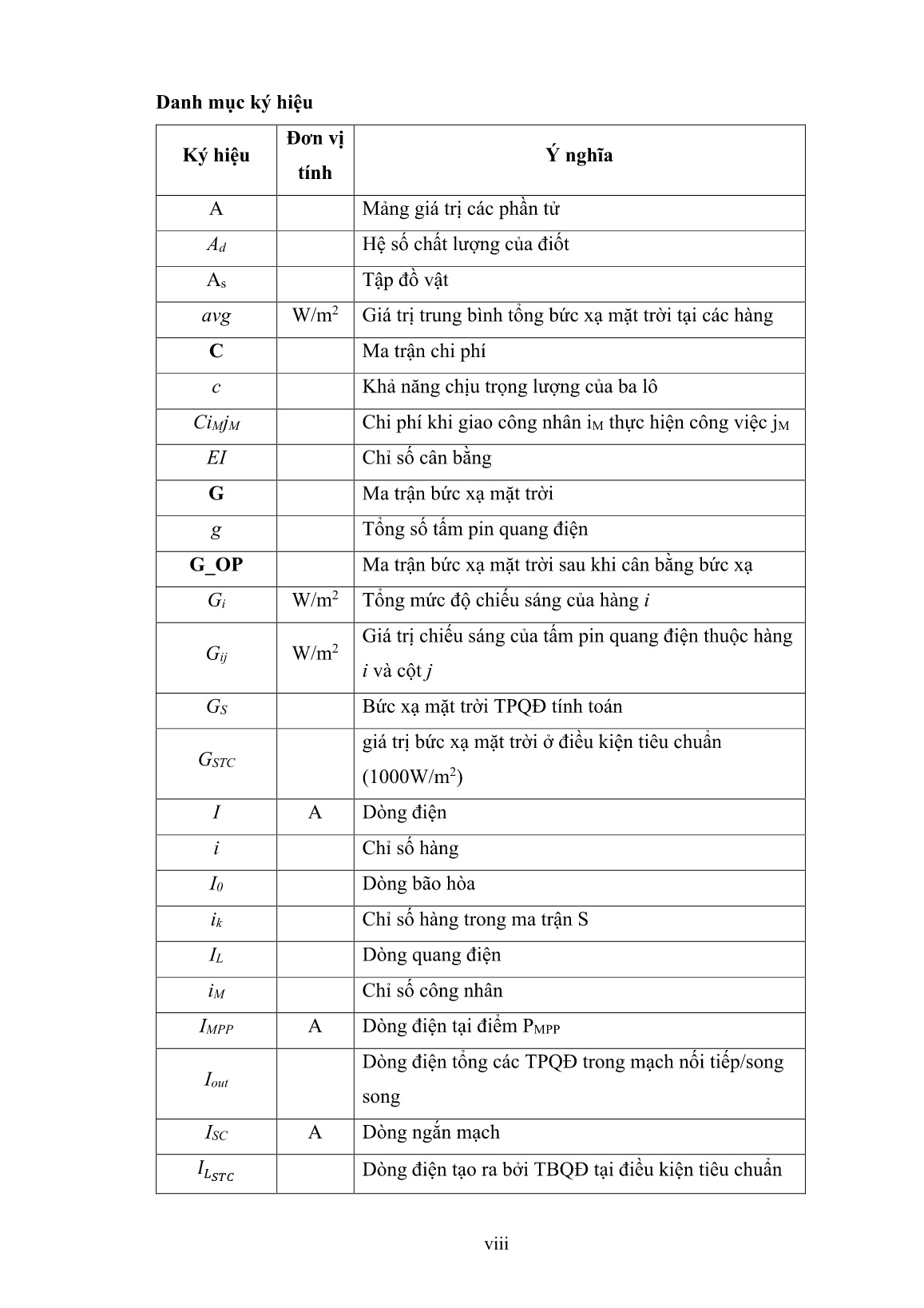
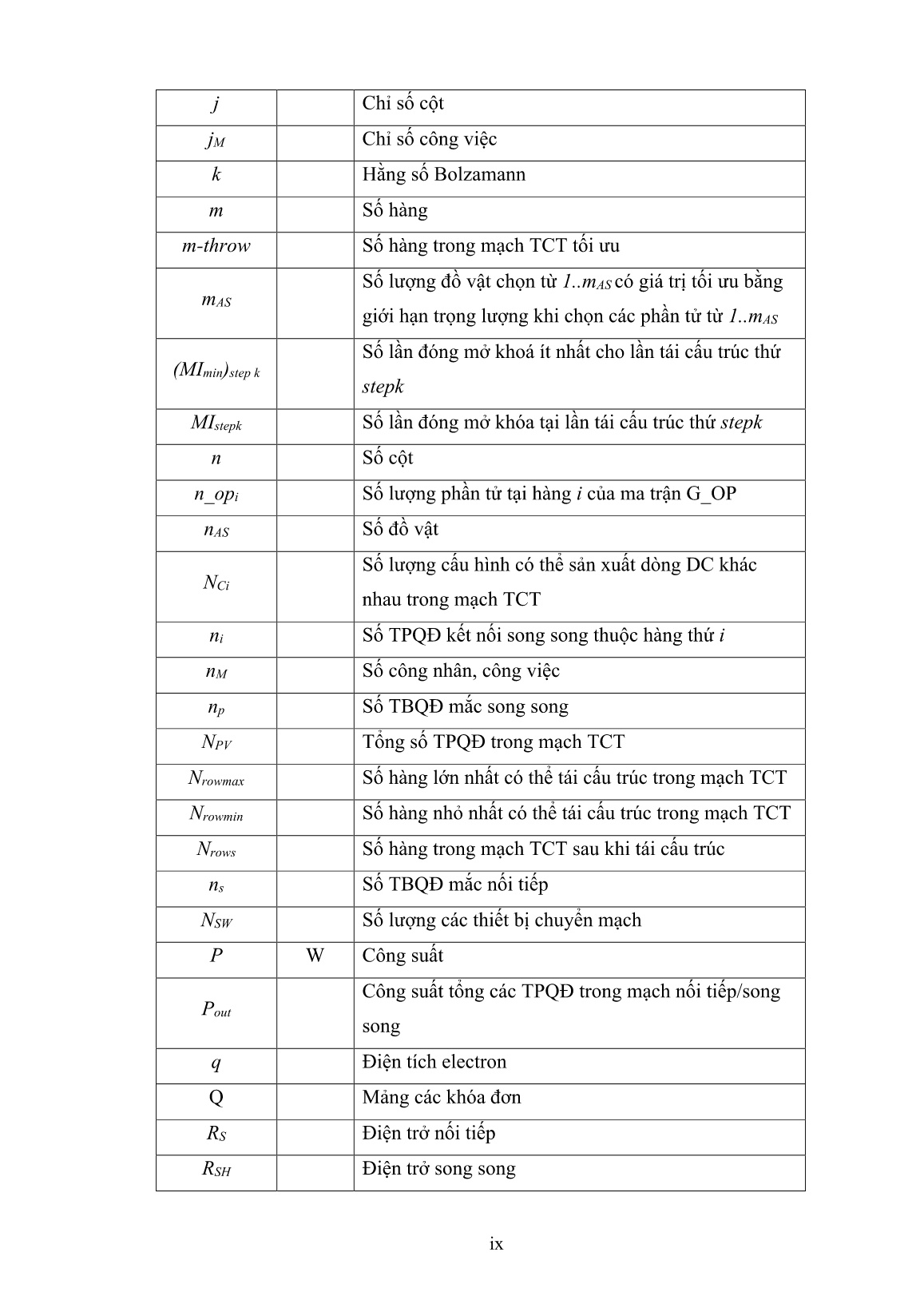
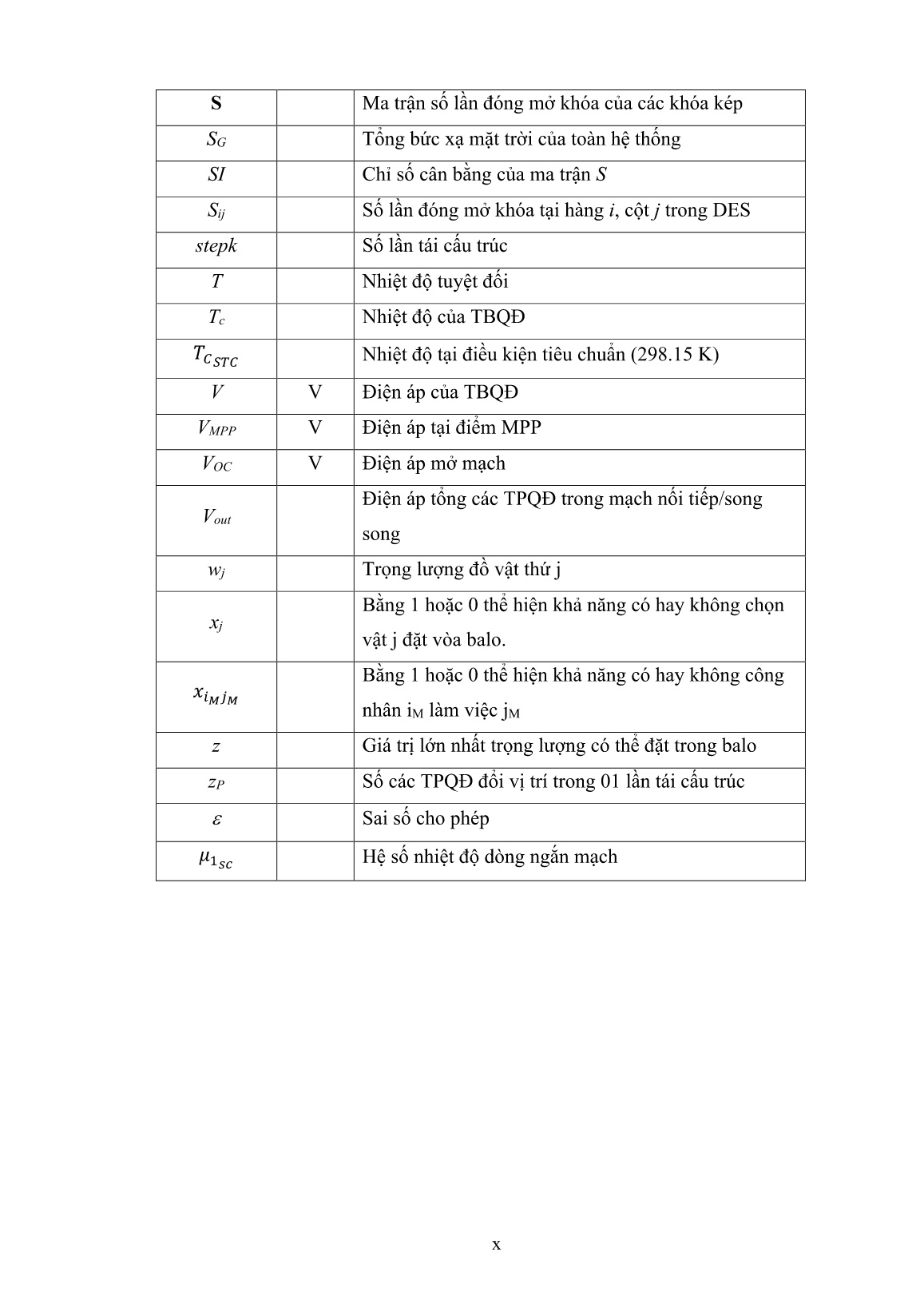
Luận án Đề xuất các thuật toán điều khiển tối ưu cho bài toán tái cấu trúc hệ thống pin mặt trời

h và điều khiển tối ưu động. 
2.1.1 Điều khiển tối ưu tĩnh 
Bài toán điều khiển tối ưu tĩnh là bài toán trong đó quan hệ vào, ra và biến 
trạng thái của mô hình không phụ thuộc vào thời gian. Giá trị đầu ra tại một thời 
điểm chỉ phụ thuộc vào các giá trị đầu vào và trạng thái tại thời điểm đó. 
Mô hình hệ thống được cho như sau: 
yk = fk(u1, u2, ... , ur) với k = 1, 2, ..., m ( 2-1 ) 
viết gọn lại thành y = f(u). 
 58 
Hàm mục tiêu như sau: 
Q = Q(u,y) ( 2-2 ) 
Thay y = f(u) và hàm mục tiêu được: 
Q = Q(u,y) = Q(u,f(u)) = Q(u) ( 2-3 ) 
như vậy Q chỉ phục thuộc và các đầu vào và đầu ra. 
Với bài toán điều khiển tối ưu tĩnh, đây chính là bài toán cực trị với những 
điều kiện ràng buộc. Có nhiều phương pháp giải bài toán cực trị, ở đây chúng ta 
chủ yếu nghiên cứu các phương pháp phi tuyến, đó là các phương pháp: 
• Các phương pháp không dùng đạo hàm riêng. 
• Phương pháp Newton-Raphson 
• Phương pháp sử dụng hàm phạt và hàm chặn 
2.1.2 Điều khiển tối ưu động 
Bài toán điều khiển tối ưu động là bài toán trong đó mô hình toán học có 
ít nhất một phương trình vi phân. x*+xy = z+v*, {w ( 2-4 ) 
Cho mô hình hệ thống như sau: *̇+ = z+(*/, *Z,  , *>, {/, {Z,  , {}) với i = 1..n ( 2-5 ) 
viết gọn thành: *̇ = zv*, {w. 
Các đầu ra của hệ thống là: 
 59 
~ = v*, {w với ~ = (~/, ~Z,  , ~d) ( 2-6 ) 
 Hàm mục tiêu được định nghĩa như sau: 
Ä = Åz4()W *, {)xy ( 2-7 ) 
trong đó: T là thời gian xảy ra quá trình tối ưu. 
Với bài toán tối ưu động có các phương pháp giải như sau: 
• Phương pháp biến phân kinh điển. 
• Phương pháp cực đại của Pontrjagin. 
• Phương pháp quy hoạch động của Bellman. 
2.2 Thiết lập bài toán điều khiển tối ưu 
2.2.1 Cấu trúc điều khiển trong hệ thống NLMT 
Mặc dù các cấu trúc mạch lực rất đa dạng, nhưng đều có đặc điểm chung 
về sơ đồ khối chức năng điều khiển ứng dụng cho pin mặt trời chỉ ra trên Hình 
2-1 [58]. Trong đó, một hệ thống điều khiển điện tử công suất cho pin mặt trời 
được chia làm ba cấp chức năng như dưới đây. 
+ Điều khiển cấp 1 (basic functions): Vòng điều khiển phía trong với các 
mạch vòng điện áp, dòng điện và điều chế độ rộng xung cho thiết bị biến đổi 
công suất. Xuất hiện thuật toán vòng khóa pha PLL đồng bộ điện áp lưới cho các 
yêu cầu nối lưới. 
+ Điều khiển cấp 2 (PV specific funtions): Cấp điều khiển đặc trưng của 
pin mặt trời như: thuật toán xác định điểm làm việc có công suất lớn nhất MPPT 
(maximum power point tracking), bảo vệ chống cô lập (anti – islanding) và giám 
sát, chẩn đoán lỗi của pin mặt trời. 
 60 
+ Điều khiển cấp 3 (ancillary functions): Dựa trên đặc điểm cấu trúc mạch 
lực và chế độ làm việc có thể tích hợp thêm các chức năng cho hệ thống điều 
khiển điện tử công suất như: lọc tích cực, bù công suất phản kháng... Nhiệm vụ 
chính của tầng điều khiển cấp 3 là thực hiện các nhiệm vụ điều khiển mang tính 
chất điều độ, được cài đặt qua hệ thống SCADA (điều khiển giám sát), rất quan 
trọng khi hòa với lưới. 
 61 
Hình 2-1. Sơ đồ khối chức năng điều khiển ĐTCS nối lưới cho pin mặt trời 
 62 
Nghiên cứu sử dụng trong luận án đưa ra phương pháp tái cấu trúc kết nối 
các tấm pin quang điện giúp hệ thống luôn làm việc với hiệu suất cao nhất 
(optimal PV arrays reconfiguration). Bản chất của việc tái cấu trúc chính là thay 
đổi kết nối các TPQĐ bằng cách đóng mở các khóa trong ma trận chuyển mạch 
Hình 2-2 (CT1). 
(a) (b) (c) 
Hình 2-2. Tái cấu trúc các tấm pin: (a) Cấu hình kết nối TCT, (b) Ma trận 
chuyển mạch, (c) Sơ đồ kết nối động nhờ ma trận chuyển mạch 
Bộ tái cấu trúc có vị trí nằm trước inverter nhằm thay đổi kết nối của các 
TPQĐ, như vậy mạch điều khiển áp dụng trong bộ tái cấu trúc thuộc điều khiển 
cấp 2 - cấp điều khiển đặc trưng của pin mặt trời. 
2.2.2 Bộ tái cấu trúc 
Mô hình hệ thống NLMT hòa lưới có dự trữ tổng quát như Hình 1-14. Các 
TPQĐ tạo ra dòng điện 1 chiều DC, qua bộ chuyển đổi dòng điện (inverter) có 
chức năng tích điện vào ắc quy, chuyển đổi DC/AC phục vụ tải trong gia đình 
hoặc hòa lưới. 
Mục tiêu của luận án là phân tích và đưa ra các phương pháp mới cho bài 
toán tái cấu trúc hệ thống NLMT sử dụng mạch kết nối TCT dưới điều kiện chiếu 
sáng không đồng nhất dựa trên chiến lược cân bằng bức xạ (CT1..4) nhằm mục 
tiêu giảm tổn thất công suất, tăng hiệu suất làm việc của hệ thống NLMT. Thuật 
 14 
advantages and disadvantages of each method are explained. Connect solar modules are 
connected in series in order to increase the total voltage and in parallel to increase the 
total current. 
PV Reconfiguration techniques. HANOI May 2013 
Array topologies 
Figure 2-7: Connection topologies of the PV array 
1 
2 
m 
1 2 n1 
n2 
nm 
 63 
toán điều khiển tối ưu được lập trình trong thiết bị được gọi là bộ tái cấu trúc 
(reconfiguration system), lắp trước bộ chuyển đổi (inverter) nhằm mục đích nâng 
cao hiệu suất làm việc hệ thống NLMT trong điều kiện chiếu sáng không đồng 
nhất. Vị trí của bộ tái cấu trúc thể hiện trong Hình 2-3. 
Hình 2-3. Bộ tái cấu trúc trong hệ thống NLMT hòa lưới có dự trữ 
Bộ tái cấu trúc (CT1) được mô tả trong Hình 2-4 bao gồm thành phần 
chính là ma trận chuyển mạch và bộ điều khiển. Ban đầu, bộ điều khiển có chức 
năng đo đếm dòng điện, điện áp của các TPQĐ, ước tính mức độ chiếu sáng, tìm 
cấu hình kết nối cho công suất hệ thống là cao nhất. Sau đó, bộ điều khiển ra 
lệnh đóng mở các khóa trong ma trận chuyển mạch, chuyển cấu hình kết nối các 
TPQĐ từ cấu hình ban đầu đến cấu hình tối ưu. 
Chức năng chính của bộ tái cấu trúc giúp hệ thống NLMT luôn luôn hoạt 
động với công suất là cao nhất, đầu ra của bộ tái cấu trúc là dòng DC, nhiệm vụ 
đảm bảo đầu vào cho inverter hoạt động. 
Bộ tái 
cấu trúc 
 64 
Hình 2-4. Các thành phần trong bộ tái cấu trúc (CT1) 
2.2.3 Đề xuất hệ thống điều khiển 
Trong luận án, tác giả đề xuất áp dụng hệ thống điều khiển hở để xây 
dựng bộ tái cấu trúc theo lưu đồ như Hình 2-5 (CT2). 
Hình 2-5. Hệ thống điều khiển hở cho Bộ tái cấu trúc 
Trong hệ thống điều khiển hở bao gồm các thành phần: 
- Bộ thiết bị đo dòng điện, điện áp, làm tín hiện đầu vào cho bộ vi xử lý. 
- Bộ vi xử lý phân tích, tìm cấu hình kết nối tối ưu, lựa chọn phương pháp 
chuyển mạch tối ưu, gửi tín hiệu điều khiển cho bộ chuyển mạch. 
- Bộ chuyển mạch điều khiển ma trận chuyển mạch đóng mở khóa, chuyển 
cấu hình kết nối hệ thống NLMT từ ban đầu đến cấu hình kết nối tối ưu. 
 65 
2.2.4 Đề xuất phương pháp điều khiển tối ưu 
Hình 2-6. Lưu đồ phương pháp điều khiển tối ưu áp dụng trong bộ tái cấu trúc 
Phương pháp điều khiển tối ưu áp dụng trong bộ tái cấu trúc Hình 2-6 được 
đề xuất (xem CT2) bao gồm 2 bài toán chính: bài toán tìm kiếm cấu hình cân 
bằng bức xạ và bài toán lựa chọn phương pháp chuyển mạch tối ưu. Dữ liệu đầu 
vào của phương pháp là bức xạ mặt trời và vị trí kết nối hiện tại của từng TPQĐ. 
Kết quả đầu ra của phương pháp là vị trí kết nối mới của từng TPQĐ. 
Như vậy, đây là bài toán trong đó quan hệ vào, ra và biến trạng thái của 
mô hình không phụ thuộc vào thời gian, giá trị đầu ra tại một thời điểm chỉ phụ 
thuộc và các giá trị đầu vào và trạng thái tại thời điểm đó. Phương pháp điều 
khiển tối ưu tĩnh được lựa chọn áp dụng cho hai bài toán tối ưu trên. 
 66 
2.3 Một số bài toán tối ưu sử dụng trong luận án 
2.3.1 Bài toán Subset sum problem 
2.3.1.1 Nội dung bài toán 
Bài toán Subset sum problem được Knapsack giới thiệu đầu tiên vào năm 
1990 [59], phát biểu như sau: 
Cho tập AS có nAS đồ vật và 1 cái ba lô, với wj là trọng lượng của đồ vật 
thứ j; c là khả năng chịu trọng lượng của ba lô; 
Yêu cầu: Chọn một số các đồ vật gần bằng c nhất, mà không được vượt 
quá c. 
Tức là tìm giá trị lớn nhất của Ç = ∑ Ñ-*->Ö#-e/ thỏa mãn điều kiện ∑ Ñ-*- ≤ á>Ö#-e/ với *- = 0	äã	1, å ∈ i = {1, . . , K?(} sao cho *- =ê1, Kế{	áℎọK	đồ	ñậy	yℎứ	å	0, Kế{	RℎôK	áℎọK	đồ	ñậy	yℎứ	å 
Tổng quát bài toán với hàm mục tiêu tối đa trọng lượng z: 
 maximize	z	 = cÑ-*->Ö#-e/ ( 2-8 ) 
Ràng buộc: 
⎩⎪⎨
⎪⎧ cÑ-*- ≤ á>Ö#-e/ 	*- = 0	äã	1,	å ∈ i = {1, . . , K?(}Ñ- ≥ 0	å ∈ i = {1, . . , K?(} 
( 2-9 ) 
Điều kiện ràng buộc trọng lượng z không vượt quá c, xj thể hiện có chọn 
đồ vật thứ j hay không và các đồ vật có trọng lượng lớn hơn hoặc bằng 0. 
 67 
2.3.1.2 Giải thuật quy hoạch động (Dynamic programming) 
Để giải bài toán Subset sub problem, Knapsack đã đề xuất sử dụng thuật 
toán quy hoạch động với nội dung sau: 
Cho 1 cặp số nguyên mAS (1 ≤ j?( ≤ K?() và á̂ (1 ≤ á̂ ≤ á), gọi zd(á̂) 
là giá trị trọng lượng tối ưu để chọn trong số các đồ vật từ {1, 2, ..., mAS} có giới 
hạn trọng lượng bằng á̂. Như vậy, giá trị trọng lượng tối ưu khi chọn trong số nAS 
đồ vật với giới hạn trọng lượng c là z>Ö#(á). 
Dễ dàng nhận thấy tại thời điểm ban đầu, nếu chỉ xét duy nhất đồ vật 1 và 
trọng lượng á̂: 
 z/(á̂) = ¢ 0Ñ/ 	 Kế{	á̂ < Ñ/;	Kế{	á̂ 	≥ Ñ/;	 ( 2-10 ) 
với việc giới hạn trọng lượng á̂, việc chọn tối ưu trong các đồ vật từ {1, 
2, ..., mAS} để có giá trị trọng lượng lớn nhất sẽ có 2 khả năng: 
- Nếu không chọn gói thứ mAS thì zdÖ#(á̂) là giá trị lớn nhất có thể bằng 
cách chọn trong số các gói {1, 2, ..., mAS - 1} với giới hạn trọng lượng là á̂. Tức 
là: 
 zdÖ#(á̂) = zdÖ#N/(á̂) ( 2-11 ) 
- Nếu có chọn gói thứ mAS (tất nhiên chỉ xét tới trường hợp này khi mà ÑdÖ#≤ á̂) thì zdÖ#(á̂)bằng giá trị gói thứ mAS là ÑdÖ# cộng với giá trị lớn nhất 
có thể có được bằng cách chọn trong số các gói {1, 2, ...,mAS - 1} với giới hạn 
trọng lượng á̂ - ÑdÖ#. Tức là về mặt giá trị thu được: 
 zdÖ#(á̂) = 	zdÖ#N/vá̂ − ÑdÖ#w + ÑdÖ# ( 2-12 ) 
Tổng kết với j?( = 2, , K?(; 
 68 
zdÖ#(á̂) = ¢ zdÖ#N/(á̂)max	(zdÖ#N/(á̂), zdÖ#N/(á̂ − ÑdÖ#) + ÑdÖ# 	 Kế{	á̂ < ÑdÖ# − 1;Kế{	á̂ 	≥ 	ÑdÖ#;	 (2-13 ) 
lặp lại cho đến khi tính được giá trị z>Ö#(á), độ phức tạp tính toán •(K?(á). 
Độ phức tạp không phải là độ đo chính xác lượng tài nguyên máy cần 
dùng, mà đặc trưng cho động thái của hệ thống khi kích thước đầu vào tăng lên. 
Chẳng hạn với thuật toán có độ phức tạp tuyến tính O(nAS), nếu kích thước đầu 
vào tăng gấp đôi thì có thể ước tính rằng tài nguyên cần dùng cũng tăng khoảng 
gấp đôi. Nhưng với thuật toán có độ phức tạp bình phương O(nAS2) thì tài nguyên 
sẽ tăng gấp bốn. 
2.3.2 Bài toán Munkres' Assignment Algorithm 
2.3.2.1 Phát biểu bài toán 
Bài toán phân công công việc lần đầu được tác giả James Munkres trình 
bày tại [60]. 
Bài toán này có nội dung như sau: Có nM công nhân (iM = 1, 2, ... , nM) và 
nM công việc (jM = 1, 2, ... , nM). Để giao cho công nhân iM thực hiện công việc 
jM cần một chi phí CiMjM ≥ 0. Vấn đề là cần giao cho người nào làm việc gì (mỗi 
người chỉ làm một việc, mỗi việc chỉ do một người làm) sao cho chi phí tổng 
cộng nhỏ nhất? 
Ma trận C tổng quát Hình 2-7: 
Công 
nhân 
Công việc 
1 2 ... nM 
1 C11 C12 ¶/>, 
2 C21 C22 ¶Z>, 
... 
nM ¶>,/ ¶>,Z ¶>,>, 
Hình 2-7. Ma trận chi phí C dạng tổng quát 
 69 
Mô hình toán học của bài toán như sau: 
 Çß = c c ¶+,-,*+,-,>,-,e/
>,
+,e/ → j©K ( 2-14 ) 
Với các điều kiện: 
 c *+,-,>,-,e/ = 1	, ©ß = 	1,  , Kß 
(mỗi công nhân chỉ làm một việc) 
( 2-15 ) 
 c *+,-,>,+,e/ = 1	, åß = 	1,  , Kß 
(mỗi việc chỉ do một công nhân làm) 
( 2-16 ) 
 *+,-, = 0	ℎ™~	1	, ©ß 	= 	1	,  , Kß	; 	åß 	= 	1	, 	, Kß 
(biến nhị nguyên) 
( 2-17 ) 
vì có các điều kiện ( 2-15 ) ( 2-16 ) nên điều kiện ( 2-17 ) có thể thay bằng 
 *+,-, nguyên ≥0, iM = 1 , 2 , ... , nM ; jM = 1 , 2 , ... , nM ( 2-18 ) 
2.3.2.2 Phương pháp Hungari 
Để giải bài toán MAA, Harold W. Kuhn đã đề xuất Phương pháp Hungari 
năm 1955 [61], được xây dựng trên các nguyên tắc sau: 
Nguyên tắc 1. Giả sử ma trận chi phí C của bài toán không âm và có ít 
nhất nM phần tử bằng 0. Hơn nữa nếu nM phần tử 0 này nằm ở nM hàng khác nhau 
và nM cột khác nhau thì phương án giao cho người iM thực hiện công việc tương 
ứng với số 0 này ở hàng iM sẽ là phương án tối ưu (lời giải). 
 70 
Lý giải: 
Theo giả thiết của nguyên tắc, mọi phương án giao việc có chi phí không 
âm. Trong khi đó, phương án giao việc nêu trong nguyên tắc có chi phí bằng 0, 
nên chắc chắn phương án đó là tối ưu. 
Nguyên tắc 1 cho thấy rằng ta có thể biến đổi ma trận chi phí của bài toán 
mà không làm ảnh hưởng tới lời giải của nó. Vì thế phương pháp giải sẽ thực 
hiện ý tưởng biến đổi ma trận chi phí cho đến khi đạt tới ma trận có ít nhất một 
phần tử 0 trên mỗi hàng và mỗi cột. 
Nguyên tắc 2. Cho C = ¶+,-, là ma trận chi phí của bài toán giao việc 
(nM công nhân, nM việc) và X* = +´,-,∗ là một lời giải (phương án tối ưu) của 
bài toán này. Giả sử C' là ma trận nhận được từ C bằng cách thêm số ≠ ≠ 0 
(dương hay âm) vào mỗi phần tử ở hàng r của C. Khi đó X* cũng là lời giải của 
bài toán giao việc với ma trận chi phí C'. 
Lý giải: 
Hàm mục tiêu của bài toán giao việc mới bằng: 
ÇÆ = c c ¶+,-,Æ *+,-, =>,-,e/
>,
+,e/ c c ¶+,-,*+,-, + c v¶}-, + ≠w
>,
-,e/ *}-,
>,
-,e/
>,
+,e/+,Ø}
= c c ¶+,-,*+,-, + ≠ ×>,-,e/
>,
+,e/ c *}-,
>,
+,e/ = c c ¶+,-,*+,-, + ≠
>,
-,e/
>,
+,e/ 
( 2-19 ) 
Đẳng thức cuối cùng có được là do tổng các +´,-, trên mỗi hàng, mỗi cột 
đều bằng 1. Vì thế, giá trị nhỏ nhất của z' đạt được khi và chỉ khi: 
 Ç = c c ¶+,-,*+,-,>,-,e/
>,
+,e/ 
( 2-20 ) 
là nhỏ nhất. Cụ thể là, z' đạt cực tiểu tại X = X*. 
 71 
Nguyên tắc 2 vẫn còn đúng nếu ta thêm một hằng số vào mỗi phần tử trên 
cùng một cột của ma trận chi phí. Vậy, chiến thuật của ta là biến đổi C bằng cách 
thêm hằng số vào các hàng và các cột của ma trận chi phí. 
Hình 2-8. Lưu đồ thuật toán phương pháp hungari 
Phương pháp hungari bao gồm các bước sau đây: 
Bước 0 (Bước chuẩn bị). Trừ các phần tử trên mỗi hàng của C cho phần 
tử nhỏ nhất trên hàng đó, tiếp theo trừ các phần tử trên mỗi cột cho phần tử nhỏ 
nhất trên cột đó. Kết quả ta nhận được ma trận C' có tính chất: trên mỗi hàng, 
cột có ít nhất một phần tử 0 và bài toán giao việc với ma trận C' có cùng lời giải 
như bài toán với ma trận C (nguyên tắc 2). 
Bước 1 (Đánh dấu * cho phần tử 0). Với mỗi hàng, lần lượt từ hàng 1 tới 
hàng nM, đánh dấu * cho phần tử 0 đầu tiên (trên hàng đó) không nằm trên cột 
đã có phần tử 0* (phần tử 0 được đánh dấu *). Xét hai khả năng: 
 72 
- Nếu sau khi đánh dấu thấy có đủ nM phần tử 0* thì dừng: các phần tử 0* 
sẽ cho lời giải cần tìm. Cụ thể là: người iM được giao thực hiện công việc tương 
ứng với phần tử 0* trên hàng iM (nguyên tắc 1). 
- Nếu số phần tử 0* nhỏ hơn n thì chuyển sang thực hiện bước 2. 
Bước 2. Lần lượt từ hàng 1 tới hàng nM, tìm hàng đầu tiên không chứa 
phần tử 0*, giả sử đó là hàng i0. Vì trên mỗi hàng đều có ít nhất một phần tử 0, 
nên trên hàng i0 phải có phần tử 0, chẳng hạn ở cột j0. Xuất phát từ ô (i0, j0), ta 
sẽ xây dựng một dây chuyền các ô kế tiếp nhau theo chiều dọc (theo cột), ngang 
(theo hàng) nối các phần tử 0 với 0* và 0* với 0 (gọi tắt là dây chuyền đan) nhờ 
hai thao tác: 
Bước 2.1. (Tìm 0* theo cột) Giả sử ta đang ở phần tử 0 trong ô (ik, jk) với 
k ≥ 0, ta tìm phần tử 0* trong cột jk. 
 + Nếu tìm thấy thì thêm vào dây chuyền đang xét ô chứa phần tử 
0* này, rồi thực hiện thao tác (bước 2.2) dưới đây; 
 + Nếu trái lại, ta đổi mỗi phần tử 0 trên dây chuyền đan này thành 
0* và đổi mỗi 0* (cũ) thành 0. Sau đó, nếu có đủ nM phần tử 0* thì dừng. Nếu 
chưa đủ, thì xét hàng tiếp theo không chứa 0* (nếu còn), hoặc chuyển sang bước 
3 (nếu đã xét hết). 
Bước 2.2. (Tìm 0 theo hàng) Giả sử ta đang ở phần tử 0* trong ô (ik+1, jk), 
với k ³ 0. Trên hàng ik+1 ta tìm phần tử 0 không nằm trên cột đã có mặt trong dây 
chuyền đang xét. Có hai khả năng: 
 + Nếu tìm được thì ta thêm vào dây chuyền đang xét ô chứa phần 
tử 0 này, rồi thực hiện thao tác (bước 2.1) nêu trên đây để tìm tiếp 0* theo cột. 
 + Nếu trái lại, thì ta gọi jk là cột thiết yếu và loại khỏi dây chuyền 
đang xét hai ô (ik+1, jk) và (ik, jk), tức quay lui trên dây chuyền đang xét. 
 73 
 ++ Nếu sau đó vẫn còn ô trên dây chuyền đang xét (k ≥ 1), 
ta lại xuất phát từ phần tử 0* trong ô (ik, jk-1) và lặp lại thao tác (bước 2.2) với 
hàng ik thay cho hàng ik+1, nghĩa là trên hàng ik ta tìm phần tử 0, không nằm trên 
cột jk (cột thiết yếu) và trên các cột trước đó đã có mặt trong dây chuyền đang 
xét. 
 ++ Nếu không còn ô nào trên dây chuyền này (k = 0), thì ta 
lại tìm phần tử 0 ở tương giao của hàng không chứa 0* và cột không phải là thiết 
yếu. Nếu thấy phần tử 0 như thế, chẳng hạn trong ô ( ©4Æ 	, å4Æ ), ta lặp lại thao tác 
(bước 2.1), xuất phát từ ô ( ©4Æ 	, å4Æ ). Nếu hết phần tử 0 như thế thì ta chuyển sang 
bước 3. 
Bước 3. (Xác định hàng thiết yếu) Lúc này chưa có đủ n phần tử 0* và ở 
bước 2 ta đã xác định được các cột thiết yếu. Bây giờ ta cần xác định các hàng 
thiết yếu. Một hàng gọi là thiết yếu nếu hàng đó chứa phần tử 0* ở cột không 
phải là thiết yếu. 
König, chuyên gia về lý thuyết đồ thị người Hungari, đã chứng minh 
nguyên tắc sau đây làm cơ sở lý luận cho việc biến đổi tiếp ma trận C' ở bước 4. 
Nguyên tắc 3. Số tối đa các phần tử 0* (phần tử 0 được đánh dấu *) bằng 
số tối thiểu các hàng và cột thiết yếu. Hơn nữa, số hàng và cột này chứa trọn 
mọi phần tử 0 và 0* của C'. 
Bước 4. (Biến đổi ma trận C') Giả sử a là số nhỏ nhất trong số các phần 
tử của ma trận C' thuộc hàng và cột không thiết yếu. Từ nguyên tắc 3 suy ra a 
> 0, vì mọi phần tử 0 đều nằm trên các hàng và cột thiết yếu. Biến đổi các phần 
tử trong C' bằng cách: trừ a vào mọi phần tử thuộc các hàng không thiết yếu và 
thêm a vào mọi phần tử thuộc các cột thiết yếu. Việc làm này tương đương với 
trừ a vào mọi phần tử thuộc hàng và cột không thiết yếu, và thêm a vào mọi 
phần tử thuộc hàng và cột đều là thiết yếu. Quay trở lại thực hiện bước 2 để đánh 
thêm dấu * cho các phần tử 0 trong ma trận thu được. 
 74 
Để ý rằng sau khi biến đổi ma trận C' như trên, thì trong ma trận C'' vừa 
nhận được, các phần tử 0* trong C' vẫn được giữ nguyên như cũ, và ở một số 
hàng không thiết yếu sẽ có thêm các phần tử 0 mới. Do đó tạo khả năng đánh 
thêm dấu * cho các phần tử 0 mới này. 
Thuật toán Kuhn có độ phức tạp tính toán bằng O(n3), nó rất dễ được thực 
thi và lập trình trên máy tính. 
2.3.2.3 Ví dụ 
Để minh họa cho các bước của thuật toán giải nêu trên, ta giải bài toán 
phân việc với nM = 4 và ma trận chi phí như sau: 
( 2-21 ) 
Thực hiện bước 0, ta nhận được ma trận C': Trên mỗi hàng, mỗi cột đều 
có chứa phần tử 0. 
Ở bước 1, ta đánh dấu * cho phần tử 0 ở hàng 1, cột 1 và phần tử 0 ở hàng 
2, cột 2 (vì trên cột 2 chưa có phần tử 0*). Hàng 3 và 4 chỉ có phần tử 0 ở cột 1 
mà cột này đã có 0* ở hàng 1, vì thế không thể đánh dấu * được nữa. Kết quả là 
mới có hai phần tử 0*, ta chuyển sang thực hiện Bước 2. 
( 2-22 ) 
Bước 2: Bắt đầu xét từ hàng 3, hàng chưa có phần tử 0*. Ô đầu tiên của 
hàng này chứa phần tử 0 là ô (3, 1). Ta tìm phần tử 0* trong cột 1 (thao tác A) 
và thấy 0* ở ô (1, 1), tiếp đó ta tìm phần tử 0 trong hàng 1 (thao tác B) và thấy 0 
Sӕ hya bӣi Trung tâm Hӑc OiӋX ± Ĉҥi hӑc Thii NgX\rQ  
 14 
biӃQ ÿӕi QgүX), Wӭc Oj biӃQ ÿәi Pa WUұQ C' WhjQh C" = ijc - ui - vj, sao cho ui, vj 
YүQ Oj ShѭѫQg iQ cӫa bji WRiQ ÿӕi QgүX (Wӭc C" • 0). BiӃQ ÿәi Pa WUұQ chi Sht 
ÿѭӧc Whӵc hiӋQ chR ÿӃQ khi Pa WUұQ ÿy cy ÿӫ n ShҫQ Wӱ 0* Whu dӯQg WhXұW WRiQ. 
1.3. 9Ë DӨ ÈP DӨNG 
9t Gө 1.4. ĈӇ PiQh hӑa chR cic bѭӟc cӫa WhXұW WRiQ giҧi QrX WUrQ, Wa giҧi 
bji WRiQ ShkQ YiӋc Yӟi n = 4 và Pa WUұQ chi Sht Qhѭ VaX: 
C = 
7852
4961
2623
7765
 ⇒ C' = 
5430
3650
0201
2010
. 
Thӵc hiӋQ Bѭӟc 0, Wa QhұQ ÿѭӧc Pa WUұQ C': TUrQ Pӛi hjQg, Pӛi cӝW ÿӅX 
cy c ӭa ShҫQ Wӱ 0. 
Ӣ Bѭӟc 1, Wa ÿiQh dҩX * chR ShҫQ Wӱ 0 ӣ hjQg 1, cӝW 1 Yj ShҫQ Wӱ 0 ӣ 
hjQg 2, cӝW 2 (Yu WUrQ cӝW 2 chѭa cy ShҫQ Wӱ 0*). HjQg 3 Yj 4 chӍ cy ShҫQ Wӱ 0 
ӣ cӝW 1 Pj cӝW Qj\ ÿm cy 0* ӣ hjQg 1, Yu WhӃ kh{Qg WhӇ ÿiQh dҩX * ÿѭӧc Qӳa. 
KӃW TXҧ Oj Pӟi cy hai ShҫQ Wӱ 0*, Wa chX\ӇQ VaQg Whӵc hiӋQ Bѭӟc 2. 
C' = 
5430
3650
0201
2010
. 
Bѭӟc 2: BҳW ÿҫX [pW Wӯ hjQg 3, hjQg chѭa cy ShҫQ Wӱ 0*. Ð ÿҫX WirQ cӫa 
hjQg Qj\ chӭa ShҫQ Wӱ 0 Oj { (