Luận án Tìm kiếm ảnh dựa trên đồ thị chữ ký nhị phân

¥y S-Tree (M.A. Nascimento, 2002 ) là c¥y nhi·u nh¡nh c¥n b¬ng theo chi·u cao.
Méi nút trong c¥y S-Tree gồm nhi·u chú ký li¶n k¸t đến c¡c nút con. Méi ph¦n tû cõa
nút l¡ gồm chú ký và định danh cõa đối tưñng.
2.6. C¥y Sig-Tree
2.6.1. Giới thi»u c¥y Sig-Tree
 Méi nút trong c¥y Sig-Tree gồm hai thành ph¦n để li¶n k¸t đến nút cha và li¶n k¸t
đến c¡c nút con. Ph¦n này thi¸t k¸ c§u trúc và c¡c thao t¡c tr¶n c¥y Sig-Tree gồm:
ch±n nút, lo¤i bỏ nút, t¡ch nút và t¼m ki¸m tr¶n c¥y.
2.6.2. Thi¸t k¸ c§u trúc dú li»u c¥y Sig-Tree
 Méi nút trong c¥y Sig-Tree có hai ph¦n: (1) Ph¦n li¶n k¸t đến nút cha gồm chú
ký tê hñp và ph¦n li¶n k¸t v· nút cha: hsignature; parenti; (2) Ph¦n nëi dung là tªp
c¡c chú ký và li¶n k¸t đến nút con: fSIGi = hsignaturei; nextiiji = 1; :::; kg. Méi nút
l¡ cũng gồm hai ph¦n: ph¦n li¶n k¸t nút cha hsignature; parenti và ph¦n nëi dung
fSIGi = hsignaturei; oidiiji = 1; :::; kg là tªp chú ký nhị ph¥n và định danh.
 4
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
2.6.3. Ph²p tê hñp c¡c chú ký tr¶n c¥y Sig-Tree
 Trong c¥y Sig-Tree, méi chú ký cõa nút cha là tê hñp c¡c chú ký cõa nút con. N¸u
c¡c thành ph¦n cõa nút con thay đổi th¼ ph£i tê hñp l¤i c¡c chú ký cõa nút cha và
thực hi»n cho đến nút gèc. Thuªt to¡n tê hñp chú ký được đề xu§t như sau:
Thuªt to¡n 2.5. Tê hñp chú ký
Input: Nút v c¦n tê hñp.
Output: C¥y Sig-Tree sau khi tê hñp.
Function UnionSignature(v)
 Begin
 if v ! parent 6= null then
 Signature = _(SIGi ! sig); SIGi 2 v;
 v ! parent ! (SIGi ! sig) = Signature; UnionSignature(v ! parent);
 end if
 Return Sig-Tree; End. =0
M»nh đề 2.3. Độ phùc t¤p cõa Thuªt to¡n 2.5 là O(k log n), với n là sè chú ký
tr¶n c¥y, k là chi·u dài chú ký.
2.6.4. Ph²p t¡ch mët nút tr¶n c¥y Sig-Tree
 K¸t qu£ cõa ph²p t¡ch nút là hai cụm chú ký rời nhau tương ùng với hai nút trong
c¥y Sig-Tree. Vi»c t¡ch nút làm cho c¥y Sig-Tree t«ng trưởng theo hướng gèc. Thuªt
to¡n t¡ch nút được đề xu§t như sau:
Thuªt to¡n 2.6. T¡ch nút
Input: Tªp c¡c chú ký S cõa nút c¦n t¡ch, chú ký α và β.
Output: Hai nút đã được t¡ch gồm NodeA và NodeB.
Function SplitNode(S, α, β)
 Begin
 NodeA = {α}; NodeB = {β;}
 for si 2 S do
 T½nh đë đo d(α; si) và d(β; si);
 if d(α; si) < d(β; si) then Ch±n si vào NodeA
 else Ch±n chú ký si vào NodeB;
 end if
 end for
 Return {NodeA, NodeB};
 End. =0
 5
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
Thuªt to¡n 2.7. T¡ch nút trong c¥y Sig-Tree
Input: Nút c¦n t¡ch v.
Output: C¥y Sig-Tree sau khi được t¡ch.
Function SplitTree(v)
 Begin
 T¤o tªp chú ký S cõa nút v; Tr½ch xu§t hai chú ký α, β cõa nút v;
 {NodeA, NodeB} = SplitNode(S, α, β);
 T¤o hai chú ký tê hñp SigA, SigB cõa NodeA, NodeB;
 G¡n vparent là nút cha cõa nút v;
 if (v ! parent == null) then Root = fSigA; SigBg
 else Bê sung chú ký SigA, SigB vào nút vparent; UnionSignature(v ! parent);
 if (vparent đầy) SplitTree(v ! parent); end if
 end if
 Return Sig-Tree; End. =0
M»nh đề 2.4. Độ phùc t¤p cõa Thuªt to¡n 2.6 là O(M), với M là sè chú ký.
M»nh đề 2.5. Độ phùc t¤p cõa Thuªt to¡n 2.7 là O(k(log n)2 + M log n), với
M; n; k l¦n lượt là sè chú ký tèi đa cõa nút, sè chú ký tr¶n c¥y, chi·u dài chú ký.
2.6.5. Ph²p lo¤i bỏ chú ký tr¶n c¥y Sig-Tree
 Vi»c lo¤i bỏ mët nút trong c¥y d¨n đến ph£i lo¤i bỏ mët ph¦n tû tương ùng cõa
nút cha. N¸u nút cha sau khi lo¤i bỏ có sè ph¦n tû ½t hơn sè lượng tèi thiºu th¼ ph£i
lo¤i bỏ luôn nút cha và thu gom c¡c chú ký t¤i nút l¡ theo nút cha này và thực hi»n
thao t¡c ch±n trở l¤i. Mët gi£i ph¡p đề xu§t là thực hi»n g¡n định danh đối tượng
oid = null n¸u như mët nút l¡ sau khi lo¤i bỏ có sè lượng ph¦n tû nhỏ hơn sè lượng
tèi thiºu. Khi thực hi»n thao t¡c ch±n chú ký t¤i mët nút l¡, n¸u sè lượng ph¦n tû có
oid 6= null nhi·u hơn sè lượng tèi thiºu th¼ thực hi»n lo¤i bỏ c¡c ph¦n tû có oid = null.
Thuªt to¡n 2.8. Lo¤i bỏ chú ký
Input: Chú ký Sig và nút l¡ v, sè chú ký tèi thiºu m.
Output: C¥y Sig-Tree sau khi lo¤i bỏ chú ký.
Function DeleteNode(Sig; v; m)
 Begin
 Khởi t¤o SIG = v:SIG sao cho v:SIG = Sig;
 if (v:count > m) then Lo¤i bỏ ph¦n tû SIG; UnionSignature(v)
 else v:SIG ! oid = null;
 end if
 Return Sig-Tree; End. =0
 6
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
M»nh đề 2.6. Độ phùc t¤p cõa Thuªt to¡n 2.8 là O(k log n), với n là sè chú ký
tr¶n c¥y, k là chi·u dài chú ký.
2.6.6. Ph²p ch±n chú ký tr¶n c¥y Sig-Tree
 Méi l¦n ch±n chú ký vào nút l¡ thực hi»n đếm sè ph¦n tû kh¡c trèng, n¸u vượt
qua sè lượng tèi thiºu th¼ lo¤i bỏ c¡c ph¦n tû trèng này. N¸u nút l¡ bị đầy th¼ t¡ch
nút theo Thuªt to¡n 2.7. Thuªt to¡n ch±n chú ký được đề xu§t như sau:
Thuªt to¡n 2.9. Ch±n chú ký
Input: Chú ký Sig và nút v.
Output: C¥y Sig-Tree sau khi ch±n nút.
Function InsertNode(Sig, v)
 Begin
 if (v là nút l¡) then
 Ch±n chú ký Sig vào nút v;
 if (sè lượng ph¦n tû nút v > m) then Lo¤i bỏ c¡c nút trèng; end if
 UnionSignature(v);
 if (nút v đầy) then SplitTree(v); end if
 else
 Chọn SIG 2 v : độ đo d(SIG:Sig; Sig) nhỏ nh§t;
 v = SIG ! next; InsertNode(v);
 end if
 Return Sig-Tree; End. =0
M»nh đề 2.7. Độ phùc t¤p cõa Thuªt to¡n 2.9 là O(k(log n)2 + M log n), với
M; n; k l¦n lượt là sè chú ký tèi đa cõa nút, sè chú ký tr¶n c¥y, chi·u dài chú ký.
2.6.7. T¼m ki¸m tr¶n c¥y Sig-Tree
 Luªn ¡n mô t£ vi»c t¼m ki¸m dựa tr¶n c§u trúc STACK tr¶n c¥y Sig-Tree như sau:
Thuªt to¡n 2.10. T¼m ki¸m £nh tr¶n c¥y Sig-Tree
Input: Chú ký t¼m ki¸m Sig và c¥y Sig-Tree.
Output: Tªp SigOid = fhsigi; oidii ji = 1; : : : ; pg.
Function STreeRetrieval(Sig, Sig-Tree)
 Begin
 Khởi t¤o:
 v = Root;
 SigOid = ; ; STACK = ;;
 while (not Empty(STACK )) do
 7
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
 v = Pop(STACK );
 if (v không ph£i nút l¡) then
 Chọn SIG0 2 v: d(SIG0 ! sig; Sig) nhỏ nh§t;
 Push(STACK, Sig0 ! next)
 else SigOid = SigOid [ fhv ! sigi; v ! oidii ji = 1;:::; jvjg;
 end if
 end while
 Return SigOid; End. =0
M»nh đề 2.8. Độ phùc t¤p cõa Thuªt to¡n 2.10 là O(M log n), với M là sè chú
ký tèi đa cõa nút tr¶n c¥y, n là sè chú ký tr¶n c¥y.
2.7. Thực nghi»m t¼m ki¸m £nh dựa tr¶n c¥y Sig-Tree
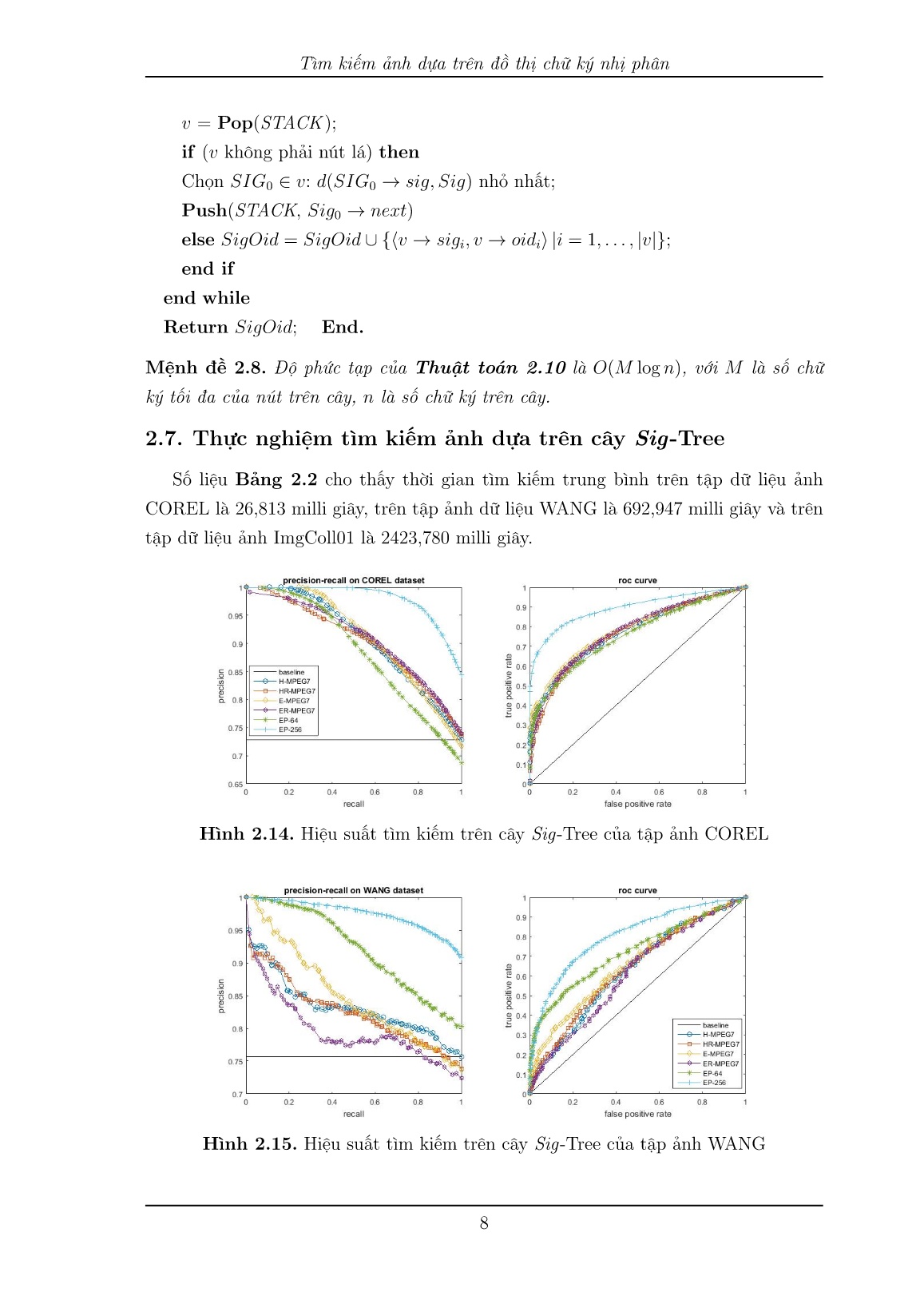
 Sè li»u B£ng 2.2 cho th§y thời gian t¼m ki¸m trung b¼nh tr¶n tªp dú li»u £nh
COREL là 26,813 milli gi¥y, tr¶n tªp £nh dú li»u WANG là 692,947 milli gi¥y và tr¶n
tªp dú li»u £nh ImgColl01 là 2423,780 milli gi¥y.
 H¼nh 2.14. Hi»u su§t t¼m ki¸m tr¶n c¥y Sig-Tree cõa tªp £nh COREL
 H¼nh 2.15. Hi»u su§t t¼m ki¸m tr¶n c¥y Sig-Tree cõa tªp £nh WANG
 8
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
 H¼nh 2.16. Hi»u su§t t¼m ki¸m tr¶n c¥y Sig-Tree cõa tªp £nh ImgColl01
 B£ng 2.2. Đánh gi¡ hi»u su§t giúa c¡c phương ph¡p tr¶n c¡c tªp dú li»u £nh
 B£ng 2.3. So s¡nh hi»u su§t t¼m ki¸m giúa c¡c phương ph¡p
 K¸t qu£ thực nghi»m được so s¡nh với c¡c phương ph¡p kh¡c đã công bè tr¶n tªp
dú li»u £nh COREL. Sè li»u so s¡nh tø B£ng 2.3 cho th§y phương ph¡p t¼m ki¸m
£nh theo nëi dung dựa tr¶n chú ký nhị ph¥n và c¥y Sig-Tree có thời gian t¼m ki¸m
nhanh hơn và độ ch½nh x¡c không k²m hơn c¡c phương ph¡p kh¡c.
2.8. Têng k¸t chương
 Chương 2 đã ti¸p cªn phương ph¡p t¼m ki¸m £nh dựa tr¶n chú ký nhị ph¥n và
c¥y Sig-Tree. K¸t qu£ thực nghi»m cho th§y phương ph¡p đ· xu§t là gi£i ph¡p hi»u
qu£ để t¼m ki¸m £nh theo nëi dung. Tuy nhi¶n, qu¡ tr¼nh truy t¼m cụm phụ thuëc vào
c¡c mùc tr¶n c¥y và ph²p t¡ch gh²p có thº £nh hưởng tr¶n toàn bë c¥y Sig-Tree. V¼
vªy, luªn ¡n thực hi»n c£i ti¸n phương ph¡p b¬ng c¡ch ph¥n cụm dựa tr¶n c§u trúc
đồ thị nh¬m t«ng độ ch½nh x¡c t¼m ki¸m £nh.
 9
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
Chương 3. ĐỀ XUẤT PHƯƠNG PHÁP TÌM KIẾM ẢNH
 DỰA TRÊN ĐỒ THỊ CHỮ KÝ
3.1. Giới thi»u
 Chương này x¥y dựng c§u trúc đồ thị S-kGraph và m¤ng Sig-SOM tr¶n cơ sở gom
cụm chú ký nhị ph¥n. Tø đó, luªn ¡n tr¼nh bày c¡c thuªt to¡n và thực nghi»m cho
phương ph¡p t¼m ki¸m £nh dựa tr¶n chú ký nhị ph¥n.
3.2. Chú ký nhị ph¥n cõa h¼nh £nh
Định nghĩa 3.1. Chú ký nhị ph¥n cõa đối tượng đặc trưng O tr¶n £nh I là mët chuéi
 O O O O O
bit SigI = b1 b2 :::bN , sao cho bi = 1 n¸u khèi thù i cõa £nh I và vùng đặc trưng O có
 O
di»n t½ch giao nhau lớn hơn ngưỡng θ cho trước, bi = 0 n¸u ngược l¤i; với N = n × k
là sè lượng c¡c khèi £nh.
 O O O O C C C C
Định nghĩa 3.2. Gọi SigI = b1 b2 :::bN và SigI = b1 b2 :::bM l¦n lượt là chú ký nhị
ph¥n đối tượng và chú ký nhị ph¥n màu s­c. Khi đó, chú ký nhị ph¥n cõa h¼nh £nh I
được định nghĩa là:
 O O O O O C C C
 Sig(I) = SigI ⊕ SigI = b1 b2 :::bN b1 b2 :::bM (3.1)
 Chú ký nhị ph¥n cõa h¼nh £nh gồm: (1) d¢y N-bit mô t£ chú ký nhị ph¥n đối
tượng; (2) d¢y M-bit mô t£ chú ký nhị ph¥n màu s­c (đã tr¼nh bày ở Chương 2).
3.3. Độ đo tương tự
 O C O C
Định nghĩa 3.3. Gọi Sig(I) = SigI ⊕ SigI và Sig(J) = SigJ ⊕ SigJ l¦n lượt là chú
ký nhị ph¥n cõa hai h¼nh £nh I và J. Độ đo tương tự cõa đối tượng đặc trưng và màu
 O O C C
s­c là µO(sigI ; sigJ ) và µC (sigI ; sigJ ) được x¡c định như sau:
 N
 O O 1 P O O
 µO(sigI ; sigJ ) = N (sigI [i]XORsigJ [i]) (3.2)
 i=1
 M
 C C 1 P C C
 µC (sigI ; sigJ ) = M (sigI [i]XORsigJ [i]) (3.3)
 i=1
M»nh đề 3.1. Độ tương tự µα trong Định nghĩa 3.3 (với α 2 fO; Cg) là mët
kho£ng c¡ch trong không gian metric.
Định nghĩa 3.4. Cho hai h¼nh £nh I và J l¦n lượt có chú ký nhị ph¥n là Sig(I) =
 O C O C
SigI ⊕ SigI và Sig(J) = SigJ ⊕ SigJ . Độ đo tương tự giúa hai h¼nh £nh I và J được
định nghĩa:
 O O C C
 φ(I;J) = α×(µO(sigI ; sigJ ))+β×(µC (sigI ; sigJ )) (3.4)
với α; β 2 (0; 1) là c¡c h» sè điều ch¿nh và α + β = 1.
 10
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
M»nh đề 3.2. Độ đo tương tự φ(I;J) trong Định nghĩa 3.4 là mët kho£ng c¡ch
trong không gian metric.
3.4. T¼m ki¸m £nh dựa tr¶n gom cụm chú ký nhị ph¥n
3.4.1. Gom cụm chú ký nhị ph¥n
 Méi ph¦n tû gồm chú ký nhị ph¥n sig và định danh oid. Ph¦n tû hsig; oidi được
ph¥n bè vào mët cụm n¸u kho£ng c¡ch d đến t¥m cụm này là ng­n nh§t và nhỏ hơn
ngưỡng θ. N¸u kho£ng c¡ch d lớn hơn θ th¼ ph¦n tû hsig; oidi t¤o mët t¥m cụm mới.
Thuªt to¡n 3.1. Gom cụm chú ký nhị ph¥n
Input: Ngưỡng tương tự θ và tªp chú ký h¼nh £nh Γ.
Output: Tªp c¡c cụm Ω.
Function SignatureClustering(θ, Γ)
 Begin
 Khởi t¤o Ω = ;;
 for hsig; oidi 2 Γ do
 if (Ω = ;) then Khởi t¤o cụm V0 với t¥m hsig; oidi
 else T¼m Vk 2 Γ: φ(sig; sigk) = minφ(sig; sigi); i = 1; : : : ; m; end if
 if (φ(sig; sigk) < θ) then Vk = Vk [ fhsig; oidig; Cªp nhªt l¤i t¥m cụm;
 else T¤o mới cụm V có t¥m hsig; oidi; Bê sung tªp cụm Ω = Ω [ V ; end if
 end for
 Return Ω; End. =0
M»nh đề 3.3. Độ phùc t¤p cõa Thuªt to¡n 3.1 là O(N 2), với N là sè lượng ph¦n
tû cõa tªp chú ký Γ.
3.4.2. Thuªt to¡n t¼m ki¸m £nh
 Qu¡ tr¼nh t¼m ki¸m £nh đưñc thực hi»n b¬ng c¡ch chọn ra cụm có t¥m g¦n nh§t
với h¼nh £nh tra cùu. N¸u kho£ng c¡ch này nhỏ hơn ngưỡng θ th¼ thực hi»n tr½ch xu§t
c¡c định danh oid trong tªp cụm và s­p x¸p theo độ đo tương tự. Thuªt to¡n t¼m
ki¸m £nh được đề xu§t như sau:
Thuªt to¡n 3.2. T¼m ki¸m £nh
Input: Chú ký £nh sig, tªp cụm Ω và ngưỡng t¼m ki¸m θ.
Output: Tªp c¡c định danh £nh tương tự Ψ.
Function ClusterRetrieval(sig, Ω, θ)
 Begin
 Khởi t¤o Ψ = ;; T¼m cụm Vk : φ(sig; sigk) = minφ(sig; sigi); i = 1; ::; m;
 11
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
 if (φ(sig; sigk) < θ) then Chọn cụm Vk 2 Ω để truy hồi h¼nh £nh tương tự; end if
 Thực hi»n tra cùu £nh tương tự;
 Return Ψ; End. =0
M»nh đề 3.4. Độ phùc t¤p cõa Thuªt to¡n 3.2 là O(m), với m là sè lượng cụm.
3.4.3. Thực nghi»m t¼m ki¸m £nh dựa tr¶n gom cụm
 H¼nh 3.2. Mô h¼nh t¼m ki¸m £nh dựa tr¶n gom cụm chú ký nhị ph¥n
 H¼nh 3.9. Hi»u su§t t¼m ki¸m dựa tr¶n gom cụm tªp £nh CBIRimages
3.5. X¥y dựng đồ thị S-kGraph
3.5.1. C§u trúc đồ thị S-kGraph
Định nghĩa 3.5. Đồ thị chú ký là đồ thị vô hướng SG = (V; E), trong đó, tªp c¡c
đỉnh V và tªp c¡c c¤nh E được định nghĩa như sau:
 V = fvI = hsigI ; oidI ijI 2 =g (3.6)
 E = fhvI ; vJ ijφ(I;J) ≤ θ; 8I;J 2 =g (3.7)
với I, J là hai h¼nh £nh trong tªp £nh =; φ(I;J) là độ đo tương tự; θ là gi¡ trị ngưỡng.
 Ph¦n này x¥y dựng đồ thị S-kGraph với méi đỉnh là mët cụm dựa tr¶n độ đo φ.
Định nghĩa 3.6. Mët cụm V có t¥m I được định nghĩa:
 V = fJjφ(I;J) ≤ kθ; J 2 =g (3.8)
với kθ là b¡n k½nh cụm V , = là tªp dú li»u £nh, k 2 N ∗.
 12
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
 H¼nh 3.10. Hi»u su§t t¼m ki¸m dựa tr¶n gom cụm tªp £nh COREL và WANG
 B£ng 3.4. Hi»u su§t t¼m ki¸m trung b¼nh dựa tr¶n gom cụm c¡c tªp £nh
 B£ng 3.5. So s¡nh độ ch½nh x¡c t¼m ki¸m tr¶n tªp £nh COREL
 Cho trước tªp Ω = fViji = 1; :::; ng là tªp c¡c cụm rời nhau, đồ thị S-kGraph được
định nghĩa như sau:
Định nghĩa 3.7. Đồ thị S-kGraph=(VSG;ESG) là mët đồ thị vô hướng, trong đó tªp
đỉnh VSG = Ω và tªp c¤nh ESG được x¡c định như sau:
 ESG = fhVi;Vjiji 6= j; Vi;Vj 2 VSG; φ(Ii0 ;Jj0 ) < kθg (3.9)
 Gọi I0 là £nh c¦n ph¥n bè vào tªp cụm rời nhau Ω. Gọi Im là t¥m cõa cụm Vm sao
cho: (φ(I0;Im) − kmθ) = minf(φ(I0;Ii) − kiθ); i = 1; :::; ng, với Ii là t¥m cõa cụm Vi.
Quy t­c 3.1. Quy t­c ph¥n bè h¼nh £nh:
 (1) N¸u φ(I0;Im) ≤ kmθ th¼ £nh I0 được ph¥n bè vào cụm Vm.
 (2) N¸u φ(I0;Im) > kmθ th¼ đặt k0 = [(φ(I0;Im) − kmθ)/θ], khi đó:
 (2.1) N¸u k0 > 0 th¼ t¤o cụm V0 t¥m I0, b¡n k½nh k0θ và Ω = Ω [ fV0g;
 13
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
 (2.2) Ngược l¤i (k0 = 0), £nh I0 ph¥n bè vào cụm Vm và g¡n φ(I0;Im) = kmθ.
 Để tr¡nh xung đột dú li»u, c¡c h¼nh £nh n¸u được ph¥n bè th¼ ph£i thuëc v· mët
cụm duy nh§t. C¡c định lý sau đây chùng minh v· sự ph¥n bè duy nh§t này.
Định lý 3.1. Cho đồ thị S-kGraph=(VSG;ESG). Gọi hVi;Vji 2 ESG và Ii0 ;Jj0 l¦n lượt
là t¥m cõa Vi;Vj. Khi đó ta có:
 φ(Ii0 ;Jj0 ) > (ki0 + kj0 )θ (3.10)
với 8I 2 Vi; φ(Ii0 ;I) ≤ ki0 θ và 8J 2 Vj; φ(Jj0 ;J) ≤ kj0 θ.
Định lý 3.2. Méi £nh I ch¿ được ph¥n bè vào mët cụm duy nh§t trong tªp Ω =
fViji = 1; :::; ng.
Định lý 3.3. Với méi £nh I, gi¡ trị φ(I;Im) − kmθ ≤ 0 ch¿ x£y ra duy nh§t t¤i Im.
Định lý 3.4. Cho tªp Ω = fViji = 1; :::; ng là tªp c¡c cụm, gọi I là mët h¼nh £nh b§t
kỳ. Khi đó tồn t¤i cụm Vi0 2 Ω sao cho I 2 Vi0 .
3.5.2. Thuªt to¡n t¤o đồ thị S-kGraph
 Đồ thị S-kGraph được x¥y dựng tø tªp £nh = và ngưỡng θ theo Quy t­c 3.1.
Thuªt to¡n t¤o đồ thị S-kGraph được đề xu§t như sau:
Thuªt to¡n 3.3. T¤o đồ thị S-kGraph
Input: Tªp dú li»u £nh = và gi¡ trị ngưỡng b¡n k½nh θ.
Output: Đồ thị S-kGraph=(VSG;ESG).
Function CreateSkGraph(=,θ)
 Begin VSG = ;; ESG = ;; kI = 1; n = 1;
 for I(I 2 =) do
 if (VSG = ;) then
 n n
 I0 = I; r = kI θ; Khởi t¤o cụm Vn = fhI0 ; r; φ = 0ig; VSG = VSG [ Vn
 else
 n m i
 T¼m t¥m I0 :(φ(I;I0 ) − kmθ) = minf(φ(I;I0) − kiθ); i = 1; : : : ; ng;
 m
 if ((φ(I;I0 ) ≤ kmθ)) then
 m
 Vm = Vm [ fhI; kmθ; φ(I;I0 )ig;
 else
 m
 kI = [(φ(I;I0 ) ≤ kmθ)] ;
 if (kI > 0) then
 n+1 n+1
 I0 = I; r = kI θ; Khởi t¤o cụm Vn+1 = hI0 ; r; φ = 0i;
 n+1 i
 VSG = VSG [ Vn+1; ESG = ESG [ fhVn+1;Viijφ(I0 ;I0) ≤ kθ; i = 1; : : : ; n;
 n = n + 1;
 14
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
 else
 m m
 φ(I;I0 ) = kmθ; Vm = Vm [ fhI; kmθ; φ(I;I0 )ig;
 end if
 end if
 end if
 end for Return S-kGraph; End. =0
M»nh đề 3.5. Độ phùc t¤p cõa Thuªt to¡n 3.3 là O(N), với N là sè lượng ph¦n
tû cõa tªp chú ký =.
3.5.3. Thuªt to¡n t¼m ki¸m £nh tr¶n đồ thị S-kGraph
 Thuªt to¡n 3.4. Thuªt to¡n t¼m ki¸m £nh tr¶n đồ thị S-kGraph
Input: Ảnh c¦n t¼m ki¸m IQ, đồ thị S-kGraph = (VSG;ESG), gi¡ trị ngưỡng kθ.
Output: Tªp £nh tương tự IMG.
Function SkGraphRetrieval(IQ, S-kGraph,kθ)
 Begin
 IMG = ;; V = ;;
 m i m
 φ(IQ;I0 ) = minfφ(IQ;I0); i = 1; :::; ng; V = V [ Vm, với Vm là cụm có t¥m là I0 ;
 m i
 for (Vi 2 VSG) do if(φ(I0 ;I0) ≤ kθ) then V = V [ Vi; end if end for
 j j
 for (Vj 2 V ) do IMG = IMG [ fIk;Ik 2 Vj; k = 1; :::; jVjjg; end for
 Return IMG;
 End. =0
M»nh đề 3.6. Độ phùc t¤p cõa Thuªt to¡n 3.4 là O(n), với n là sè lượng đỉnh
trong đồ thị S-kGraph.
3.5.4. Ph²p ph¥n r¢ cụm trong đồ thị S-kGraph
 Mục đích cõa vi»c ph¥n r¢ cụm nh¬m ph¥n ho¤ch l¤i c¡c cụm có b¡n k½nh qu¡ lớn.
Định lý 3.5. Thuªt to¡n t¡ch cụm V thành c¡c cụm con kh¡c réng, rời nhau C =
fV1; :::; VM g, nghĩa là V = V1 [ ::: [ VM và Vi \ Vj = ;, với i 6= j và i; j 2 f1; :::; Mg.
M»nh đề 3.7. Độ phùc t¤p cõa Thuªt to¡n 3.5 là O(m × n), với m; n là sè l¦n
ph¥n r¢ và sè lượng ph¦n tû trong cụm ph¥n r¢.
3.5.5. Thực nghi»m t¼m ki¸m £nh tr¶n đồ thị S-kGraph
 Thực nghi»m t¼m ki¸m £nh tr¶n đồ thị S-kGraph gồm hai giai đoạn: T¤o đồ thị
S-kGraph tø tªp dú li»u £nh và t¼m ki¸m tªp £nh tương tự với £nh tra cùu ban đầu.
 15
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
 H¼nh 3.14. Mô h¼nh t¼m ki¸m £nh dựa tr¶n đồ thị S-kGraph
 H¼nh 3.19. Hi»u su§t t¼m ki¸m tr¶n đồ thị S-kGraph cõa tªp £nh CBIRimages
H¼nh 3.20. Hi»u su§t t¼m ki¸m tr¶n đồ thị S-kGraph cõa tªp COREL và WANG
 16
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
 H¼nh 3.22. Hi»u su§t t¼m ki¸m tr¶n đồ thị S-kGraph cõa tªp £nh MSRDI
H¼nh 3.24. Hi»u su§t t¼m ki¸m tr¶n đồ thị S-kGraph cõa tªp £nh ImageCLEF
 H¼nh 3.26. Hi»u su§t t¼m ki¸m tr¶n đồ thị S-kGraph cõa tªp £nh ImgColl02
 B£ng 3.14. Hi»u su§t t¼m ki¸m tr¶n đồ thị S-kGraph cõa c¡c tªp dú li»u £nh
 17
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
 B£ng 3.15. So s¡nh độ ch½nh x¡c t¼m ki¸m tr¶n tªp £nh COREL
3.6. X¥y dựng đồ thị S-kGraph dựa tr¶n m¤ng Sig-SOM
3.6.1. X¥y dựng c§u trúc m¤ng Sig-SOM
 Nh¬m c£i ti¸n qu¡ tr¼nh t¤o đồ thị S-kGraph và phương ph¡p t¼m ki¸m £nh, luªn
¡n x¥y dựng m¤ng Sig-SOM. M¤ng Sig-SOM có cơ ch¸ mở rëng đồ thị S-kGraph t¤i
t¦ng đầu ra theo như Quy t­c 3.1.
Định nghĩa 3.8. M¤ng Sig-SOM là m¤ng SOM, trong đó lớp đầu vào ùng với mët
chú ký nhị ph¥n Sig(I) = b1b2:::bN , bi 2 f0; 1g và lớp đầu ra gồm N thành ph¦n tương
ùng với c¡c cụm trong đồ thị chú ký S-kGraph = (VSG;ESG). Méi mët cụm thù j ở
t¦ng đầu ra được k¸t nèi đầy đủ với N thành ph¦n cõa t¦ng đầu vào. Méi cung k¸t nèi
tø thành ph¦n thù i cõa lớp đầu vào đến cụm thù j thuëc t¦ng đầu ra có mët trọng sè
k¸t nèi là wij 2 f0; 1g.
Định nghĩa 3.9. Gọi Sig(I) = b1:::bN là chú ký nhị ph¥n cõa £nh I và tªp SIG =
 0 0
fSig(I1 ); :::; Sig(In)g là tªp chú ký nhị ph¥n cõa c¡c t¥m cụm t¤i t¦ng đầu ra cõa
m¤ng Sig-SOM. Cụm chi¸n th­ng Vm ùng với dú li»u đầu vào Sig(I) = b1:::bN thỏa:
 0 0
 δ(I;Im) = maxfδ(I;Ii )ji = 1; :::; ng (3.12)
với δ(I;I0) = α × d (sigO; sigO) + β × d (sigC ; sigC ) và α; β 2 (0; 1); α + β = 1.
 i O I Ii C I Ii
 d (sigO; sigO) = 1 PN NOT (SigO[i]XORSigC [i])
 O I Ii N i=1 I Ii
 d (sigC ; sigC ) = 1 PM NOT (SigC [i]XORSigC [i])
 C I Ii M i=1 I Ii
 Khi đó, cụm chi¸n th­ng Vm là cụm k¸t nèi trực ti¸p với vec-tơ chi¸n th­ng Wm.
Định lý 3.6. N¸u Vm là cụm chi¸n th­ng ùng với dú li»u đầu vào Sig(I) = b1b2:::bN
 m
th¼ kho£ng c¡ch φ(I;I0 ) là ng­n nh§t, nghĩa là:
 m i
 φ(I;I0 ) = minfφ(I;I0)ji = 1; :::; jVSGjg (3.13)
 i
với I0 là t¥m cõa cụm Vi 2 VSG và φ là độ đo tương tự.
3.6.2. Thuªt to¡n hu§n luy»n m¤ng Sig-SOM
Quy t­c 3.2. Gọi Sig(I) = b1b2:::bN là chú ký nhị ph¥n cõa £nh I. Gọi Wm =
(w1m; w2m; :::; wNm) là vec-tơ trọng sè k¸t nèi t¤i thời điºm t. Quy t­c hu§n luy»n
m¤ng Sig-SOM t¤i thời điểm t + 1 ùng với dú li»u đầu vào Sig(I) = b1b2:::bN như sau:
 18
 T¼m ki¸m £nh dựa tr¶n đồ thị chú ký nhị ph¥n
 (t+1) (t)
 wi;m = bi _ wi;m (3.14)
 (t+1) (t)
 wi;j = :bi ^ wi;j (3.15)
với j 6= m và j = 1; :::; n
 (t)
Định lý 3.7. Đặt Sig(I) = b1:::bN là dú li»u đầu vào, Wm = (w1m; :::; wNm) là vec-tơ
trọng sè k¸t nèi t¤i thời điểm t. Ta có:
 (t) (t+1)
 δ(Sig(I);Wm ) ≤ δ(Sig(I);Wm ) (3.16)
 Thuªt to¡n 3.6. Thuªt to¡n hu§n luy»n m¤ng Sig-SOM
Input: Tªp hu§n luy»n Γ = fSig(Ii) = (bi1; bi2; :::; biN )ji = 1; :::; Kg.
Output: M¤ng Sig-SOM sau khi đã hu§n luy»n.
Function SigSOMTraining(Γ)
 Begin
 Bước 1. Khởi t¤o m¤ng
 Khởi t¤o tªp hu§n luy»n Γ gồm K vec-tơ c¡c chú ký nhị ph¥n Sig(Ii) = (bi1; :::; biN )
 mô t£ tªp c¡c h¼nh £nh ==fIiji = 1; :::; Kg; Khởi t¤o t¦ng đầu ra gồm n cụm
 Ω = fVj = hCj; kjθig, với Cj = (cj1; :::; cjN ); cjk 2 f0; 1g, k = 1; :::; N; j = 1; :::; n;
 Khởi t¤o tªp trọng sè W = fWjjWj = (w1j; :::; wnj); wij 2 f0; 1g; i = 1; :::; ng;
 Với méi chú ký nhị ph¥n đầu vào Sig(Ii) g¡n tªp S =; và