Luận án Nghiên cứu ảnh hưởng của các thông số công nghệ và nhiệt độ đến biến dạng tạo hình khi dập vuốt chi tiết dạng cốc từ vật liệu SPCC

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7
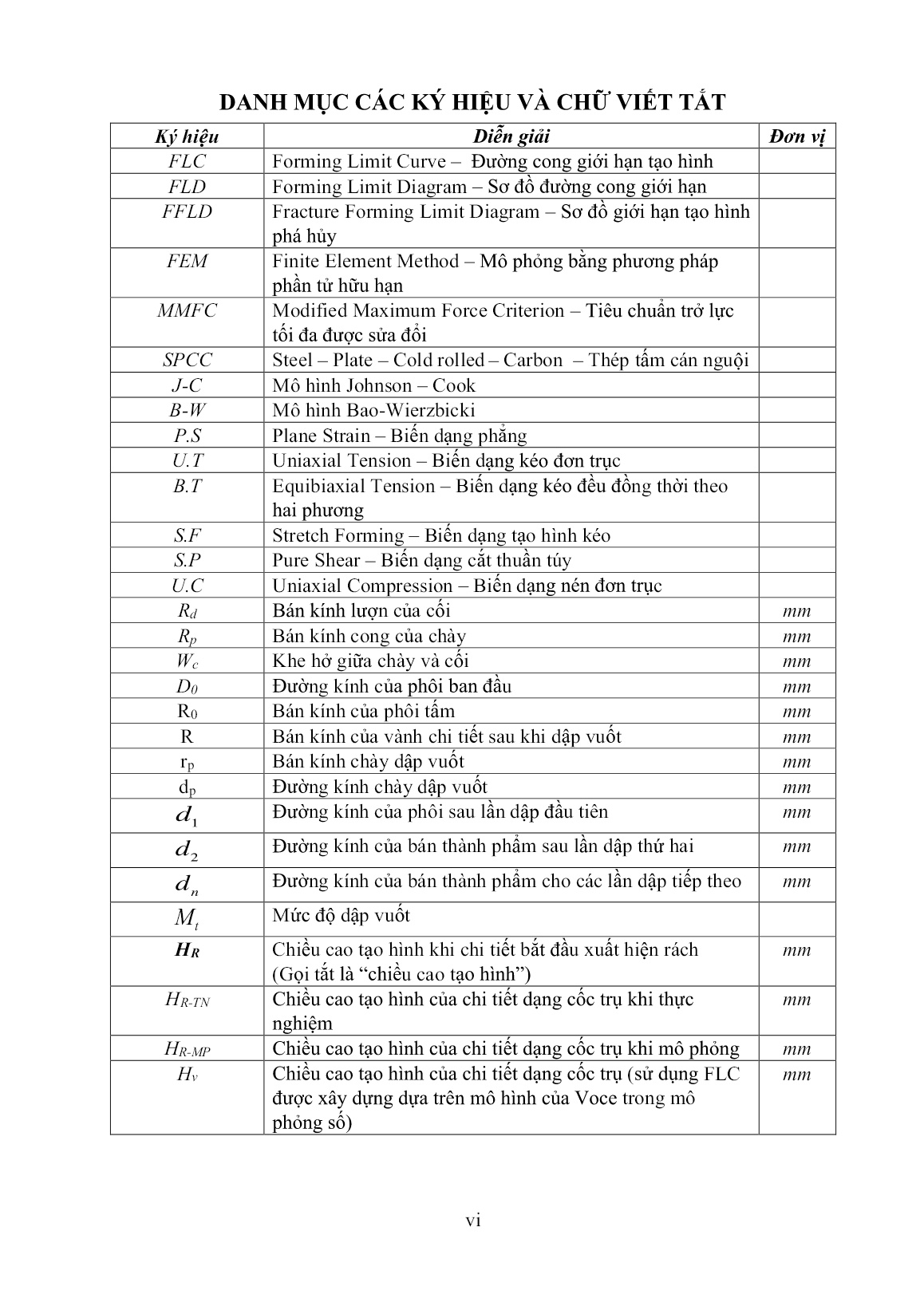
Trang 8
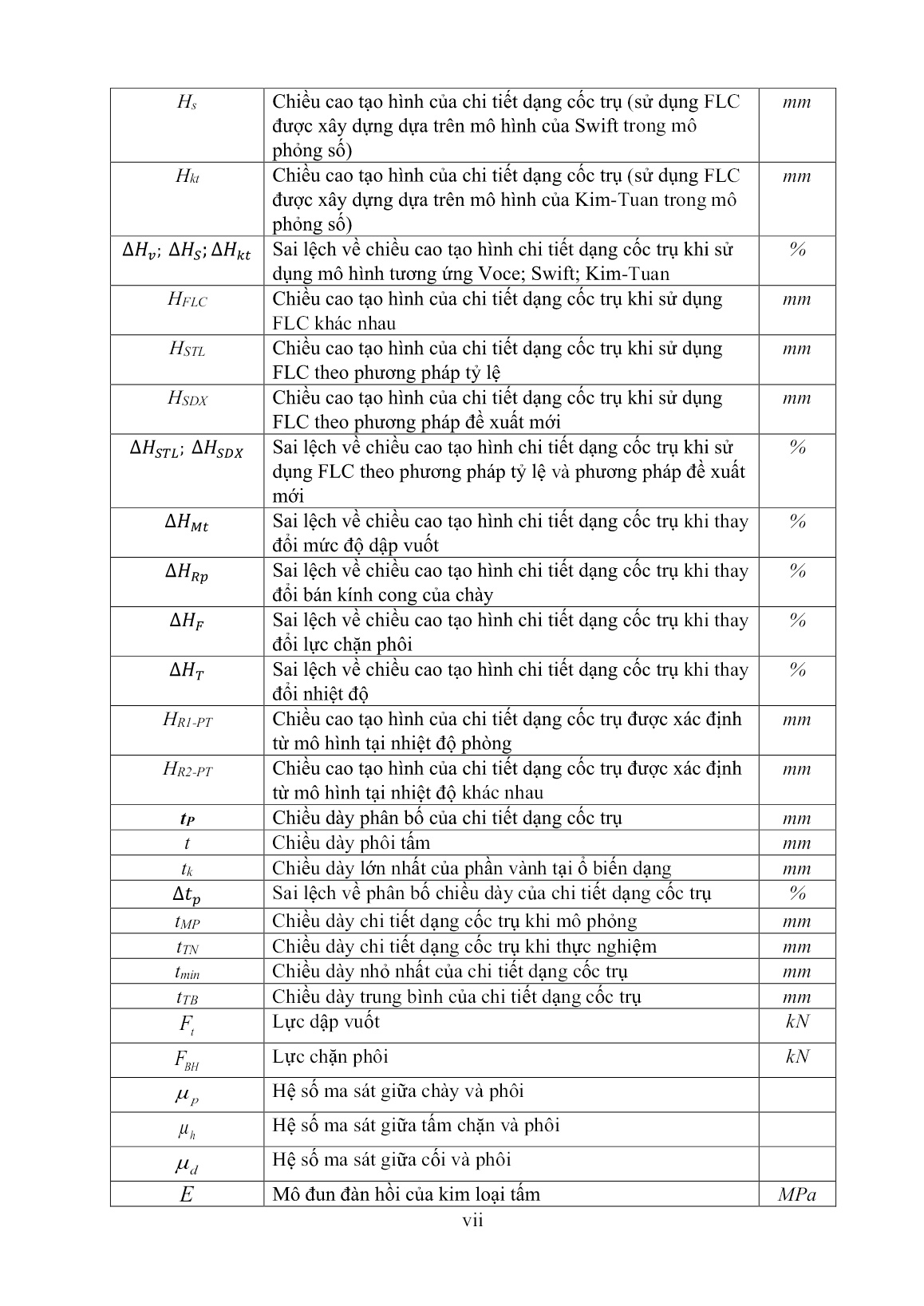
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Luận án Nghiên cứu ảnh hưởng của các thông số công nghệ và nhiệt độ đến biến dạng tạo hình khi dập vuốt chi tiết dạng cốc từ vật liệu SPCC", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Luận án Nghiên cứu ảnh hưởng của các thông số công nghệ và nhiệt độ đến biến dạng tạo hình khi dập vuốt chi tiết dạng cốc từ vật liệu SPCC

45; ; ; ( 1) 1 1 2 ( 1)90 0 0 0 90 0 r r r r r F G G N r r r r r r + + = = = = + + + + 44 2.1.3 Mô hình thuộc tính vật liệu Xét đồ thị quan hệ ứng suất - biến dạng của vật liệu (hình 2.6), phương trình thuộc tính cơ học vật liệu được thiết lập để mô tả hành vi vật liệu trên miền OBM. Ứng xử của vật liệu miền OB – đàn hồi, BM –ứng xử đàn-dẻo. Hình 2. 6 Đường cong ứng suất biến dạng của thép. Bảng 2. 2 Mô hình thuộc tính vật liệu Tác giả Phương trình Thông số vật liệu Holloman nK = ,K n (2.27) Ludwick 0 nK = + , ,0 K n (2.28) Swift ( )0 n K = + ,K n (2.29) Voce �̄� = 𝜎𝑌 + 𝑃(1 − 𝑒𝑥𝑝( − 𝑄𝜀̄)) 𝜎𝑌 , 𝑃, 𝑄 (2.30) Kim-Tuan �̄� = 𝜎0 + 𝐾(1 − 𝑒𝑥𝑝( − 𝑡𝜀̄))(𝜀̄ + 0.002) ℎ 𝜎0, 𝐾, 𝑡, ℎ (2.31) Strain rate nC = ,C n (2.32) El-Magd-Troot 0.nK = ,K n (2.33) A.D Tretiacook . .m n tK −= , , ,K n m (2.34) Ludwingson ( ) ( )0 1 2 exp( n m T T K K T − = + + , , , 1,2 K n (2.35) Zerilli- Armstrong 3 4 1/20 2 0 1 5 K T n K T K K K d e − − − = + + + 00 1 5, , K − (2.36) Johnson - Cook ( ) ( )* 0 . 1 . 1 mn p A B C ln T = + + − , , , ,A B C n m (2.37) 45 Sự hội tụ và độ chính xác của mỗi mô hình phụ thuộc vào những giả thiết cơ bản khi thiết lập mô hình như: tính liên tục trong toàn bộ thể tích vật liệu, tính bao quát các điều kiện thực tế của quá trình, sử dụng các thuật toán đơn giản, số lượng các hệ số nhỏ nhất nhưng vẫn mô tả được đầy đủ nhất các yếu tố tác động vào quá trình, các biến trong mô hình phải mang ý nghĩa vật lý đối với từng hiện tượng cụ thể. Bảng 2.2 trình bày một số mô hình thuộc tính vật liệu, mỗi mô hình đều có ưu, nhược điểm và phạm vi ứng dụng riêng. Mô hình Holloman (2.27) là một phương trình toán học đơn giản nhất, phương trình mô tả mức độ biến dạng của ứng suất chảy là mô hình Ludwick (2.28) và Swift (2.29), Voce (2.30), Kim-Tuan (2.31) hai mô hình này áp dụng cho biến dạng nguội, có tính tới yếu tố tác động của ứng suất chảy ban đầu của vật liệu. Ưu điểm của những mô hình này là sự đơn giản, dễ nhận dạng, sử dụng trong mô phỏng các bài toán yêu cầu độ chính xác không cao. Nhược điểm của các mô hình là chỉ mô tả hành vi cơ học của vật liệu ở trạng thái nguội, trong khi đa số các bài toán tạo hình vật liệu ở nhiệt độ biến đổi. Bên cạnh các mô hình biểu diễn sự ảnh hưởng của mức độ biến dạng, các mô hình tính đến ảnh hưởng của tốc độ biến dạng (2.32), (2.33), (2.34). Nguyên lý chuyển động trong môi trường nhớt cho thấy, ứng suất chảy tăng khi tốc độ biến dạng tăng, mô hình đơn giản nhất là công thức (2.32) với 𝜎 = 𝐶 ∙ 𝜀�̇�, trong đó C là hằng số hóa bền, phụ thuộc vào biến dạng, nhiệt độ và vật liệu; n là hằng số của ứng suất với tốc độ biến dạng. Mô hình Ludwingson, Zerilli-Armstrong đã tính đến ảnh hưởng của thông số nhiệt độ khi thiết lập (2.35), (2.36). Hai tác giả đã mô hình hóa sự tác động của nhiệt độ đến hành vi của vật liệu trong quá trình biến dạng lớn. Các mô hình có thể áp dụng cho bài toán tạo hình ở nhiệt độ cao, các bài toán va đập. Tuy nhiên, nhận dạng các hệ số của mô hình phức tạp, đòi hỏi phải có các thiết bị thí nghiệm đặc biệt. Quá trình tạo hình vật liệu kim loại thường chịu tác động của ba yếu tố chính là mức độ biến dạng, tốc độ biến dạng và nhiệt độ. Một trong các mô hình xét đến cả ba thông số này là mô hình thuộc tính Johnson – Cook (2.37). Thực tế, khi tăng nhiệt độ, các tính chất của kim loại thay đổi, chúng trở nên mềm dẻo và dễ biến dạng hơn. Biến dạng dẻo làm cho mật độ các khuyết tật mạng tăng lên, do đó năng lượng trong vật thể cũng thay đổi. 2.1.4 Xác định cơ tính vật liệu SPCC sử dụng trong nghiên cứu Với mục tiêu là nghiên cứu quá trình tạo hình chi tiết dạng cốc trụ bằng công nghệ dập vuốt, luận án tập trung nghiên cứu các thông số ảnh hưởng tới quá trình tạo hình của chi tiết tại nhiệt độ phòng và nhiệt độ khác nhau nên việc xác định cơ tính của vật liệu thực nghiệm là cần thiết. Kết quả này sẽ được sử dụng trong mô phỏng số quá trình tạo hình chi tiết nhằm định lượng các thông số cho quá trình thực nghiệm kiểm chứng kết quả giữa lý thuyết và thực tế. 46 Tính dị hướng của vật liệu ảnh hưởng rất lớn đến chất lượng sản phẩm dập. Trong trường hợp cơ tính của vật liệu theo 3 phương như nhau thì vật liệu mang tính đẳng hướng. Cơ tính theo các phương gồm: phương cán, phương ngang vuông góc với hướng cán và theo phương 450 so với hướng cán như Hình 2.7. Để xác định cơ tính của vật liệu SPCC, ta sử dụng thực nghiệm kéo các mẫu như Hình 2.8 với thiết bị thử kéo tại các nhiệt độ khác nhau như Hình 2.9, Hình 2.10. Các thử nghiệm kéo tại nhiệt độ phòng được tiến hành theo tiêu chuẩn ISO 6892-1, từ đó tính hệ số Lankford theo các hướng lần lượt là RD-00, RD-450, TD-900. Khi thử kéo tại nhiệt độ khác nhau các thử nghiệm được tiến hành theo tiêu chuẩn ISO 6892-2. Kết quả đường cong ứng suất biến dạng xác định tại nhiệt độ phòng được biểu diễn như trong đồ thị Hình 2.11 với tính chất vật liệu như Bảng 2.3. Kết quả đường cong ứng suất biến dạng tại nhiệt độ khác nhau được biểu diễn như trong đồ thị Hình 2.12 với tính chất vật liệu như Bảng 2.4. a) b) Hình 2. 7 (a) Sơ đồ minh họa các hướng của ba mẫu được cắt từ tấm ban đầu và (b) kích thước của mẫu thực nghiệm kéo đơn trục theo tiêu chuẩn ISO 6892 (Đơn vị: mm). a) b) c) Hình 2. 8 Mẫu thực nghiệm kéo theo 3 hướng; a, song song với phương cán (RD-00); b, vuông góc với phương cán (TD-900); c, so với phương cán 450(RD-450) 47 - Thiết bị thực nghiệm kéo (nhiệt độ phòng, nhiệt độ khác nhau) Hình 2. 9 Thí nghiệm kéo mẫu ở nhiệt độ phòng trên máy kéo nén Tinius Olsen Super L120 Hình 2. 10 Thí nghiệm kéo mẫu ở nhiệt độ khác nhau trên máy kéo nén Tinius Olsen Super L120. 48 Đồ thị quan hệ giữa ứng suất và biến dạng tại nhiệt độ phòng theo ba hướng Hình 2. 11 Đồ thị quan hệ giữa ứng suất và biến dạng tại nhiệt độ phòng theo 3 hướng: RD-00; RD-450; TD-900 Đồ thị quan hệ giữa ứng suất và biến dạng tại nhiệt độ phòng và nhiệt độ khác nhau. Hình 2. 12 Đồ thị quan hệ giữa ứng suất và biến dạng theo nhiệt độ phòng và nhiệt độ khác nhau Bảng 2. 3 Thuộc tính của SPCC tại nhiệt độ phòng Vật liệu SPCC Hướng cán 00 450 900 Ứng suất chảy (MPa) 152.1 155.6 162 Hệ số dị hướng (r) 1.82 1.67 2.17 Mật độ vật liệu (ρ kg/mm3) 7.8e-06 Mô đun đàn hồi (E, kN/mm2) 210 Hệ số Poisson 0.3 49 Bảng 2. 4 Thuộc tính của SPCC tại nhiệt độ khác nhau 2.2 Xây dựng FLC của vật liệu tấm SPCC tại nhiệt độ phòng và nhiệt độ khác nhau Các nghiên cứu lý thuyết trước đây cho thấy rằng việc tính toán FLC, dựa trên bất kỳ mô hình lý thuyết nào cũng đòi hỏi lời giải toán của một hệ thống các phương trình phức tạp, việc giải một hệ thống lớn các phương trình này là không hề dễ dàng cho dù đã có sự hỗ trợ của các phần mềm toán học. Do đó, nghiên cứu đã xây dựng sơ đồ các bước như Hình 2.13 nhằm mục đích đơn giản hóa việc xác định đường cong giới hạn tạo hình (FLC) của vật liệu. Hình 2. 13 Sơ đồ các bước xây dựng FLC tại các nhiệt độ khác nhau Vật liệu SPCC 250C 1500C 2500C Ứng suất chảy (MPa) 152.1 112.6 86.5 Độ bền kéo (MPa) 428.8 341.8 326.3 Mô đun đang hồi (E, kN/mm2) 210 171 163 Mật độ vật liệu (ρ kg/mm3) 7.8e-06 Hệ số Poat xông 0.3 50 2.2.1 Xây dựng FLC của vật liệu tấm SPCC tại nhiệt độ phòng 2.2.1.1 Phương pháp tiêu chuẩn trở lực tối đa được sửa đổi (MMFC) [5]. Trong quá trình kiểm tra độ bền kéo đơn trục, điều kiện cho lực kéo cực đại được chỉ ra như phương trình (2.38): ( ) 0dF d S Sd dS = = + = (2.38) Trong đó S biểu thị diện tích mặt cắt của mẫu thử và F là lực kéo đo được. Điều kiện được viết lại như sau: S d d dS d =− = (2.39) Dựa trên quan sát, Swift [81] đã trình bày một lý thuyết về tiêu chí lan tỏa và tiến triển vết nứt để ước tính giới hạn biến dạng dẻo thông qua đường cong giới hạn tạo hình (FLC) cho kim loại tấm. Tiêu chí này đã được công bố rộng rãi để dự đoán (FLC) của các loại vật liệu khác nhau. Sau đó, Hora cùng cộng sự [65] đã phát triển một tiêu chí được gọi là tiêu chuẩn trở lực tối đa được sửa đổi (MMFC) liên quan đến việc quan sát quá trình chuyển đổi đường biến dạng sau khi vết nứt xuất hiện. Biểu thức cho MMFC được đưa ra là: 1 1 ,1 1 1 1 1 1 d d d + (2.40) trong đó / 2 1 = biểu thị tỷ lệ biến dạng theo 2 phương chính. Giả thiết rằng / 2 1 = biểu thị tỷ lệ ứng suất theo hai phương chính; và hai hàm số 𝑓(𝛼) = 𝜎/𝜎1 và 𝑔(𝛼) = 𝛥𝜀/𝛥𝜀1 mô tả mối quan hệ giữa các thành phần ứng suất (𝜎1), biến dạng chính (𝜀1) thứ nhất so với ứng suất (𝜎) và biến dạng (𝜀) tương đương. Với mỗi hàm cứng hóa được lựa chọn cho quan hệ giữa ứng suất-biến dạng, các số hạng 𝜕𝜎1/𝜕𝜀1 và 𝜕𝜎1/𝜕𝛽1 được xác định: 1 1 ( ) '/ ( ) 1 1 g H f = = (2.41) '( ) '( )1 1 /( ) 2 2[ ( )] [ ( )] f f H f f = =− =− (2.42) Trong các phương trình (2.41 và 2.42), ( )H H = biểu thị hàm cứng hóa và 'H biểu thị độ dốc của đường cong cứng hóa. Bằng cách tuân theo quy luật cơ học môi trường liên tục, ta có: /2 2 /1 1 d d = = (2.43) Do đó, '( ) sẽ được xác định rõ ràng. Việc đánh giá của / 1 được thực hiện bằng cách sử dụng lập trình quy trình lặp. Tuy vậy, để tăng tính hiệu quả và đơn 51 giản hóa quá trình tính toán / 2 1 được lựa chọn gần đúng. Do đó đạo hàm thu được là: 1 1 − (2.44) Các phương trình (2.41 và 2.43) được thay vào phương trình (2.40) cho kết quả công thức tiêu chuẩn trở lực tối đa được sửa đổi (MMFC) là: ' 1 '( ) 1 1- ( ) ( ) '( ) 1 H f H g f (2.45) Đối với từng giá trị của , theo giá trị của trong phạm vi [-0.5, 1], nếu điểm ( , )1 2 c c vi phạm điều kiện (2.45) sẽ được xác định là một điểm trên đường cong giới hạn tạo hình (FLC). Thông thường, một chương trình theo phương pháp lập trình số sẽ được phát triển để thực hiện quy trình phân tích và tính toán (FLC) của các vật liệu được thử nghiệm. Tuy nhiên việc phát triển chương trình thông qua lập trình số là một công việc tốn nhiều công sức và thời gian thực hiện. 2.2.1.2 Phương pháp họa đồ áp dụng cho vật liệu SPCC sử dụng trong nghiên cứu. Trong nghiên cứu này sử dụng ứng suất tương đương được xác định bởi hàm ứng suất Hill 1948 với mô hình Swift [81], Voce [82] và Kim-Tuan [20] tương ứng với phương trình [(2.29)-(2.31)], được áp dụng để mô tả các thuộc tính vật liệu tấm SPCC, các thông số của mô hình vật liệu được thể hiện như trong Bảng 2.5. Swift: �̄� = 𝐶(𝜀0 + 𝜀̄) 𝑛 Voce: �̄� = 𝜎𝑌 + 𝑃(1 − 𝑒𝑥𝑝( − 𝑄𝜀̄)) Kim – Tuan: �̄� = 𝜎0 + 𝐾(1 − 𝑒𝑥𝑝( − 𝑡𝜀̄))(𝜀̄ + 0.002) ℎ Bảng 2. 5 Các thông số của phương trình Swift, Voce và Kim-Tuan cho vật liệu SPCC Swift Voce Kim-Tuan C(MPa) ε0 n σY P Q σ0 K(MPa) t h 584,4 0,002 0,3 152,1 312,3 5,796 152,1 460,2 25,86 0,48 Cụ thể, ứng suất tương đương được xác định bởi hàm ứng suất Hill 1948 được tính như sau: 2 2 2 1 2 1 2( )G F H = + + − (2.46) Trong đó G, F và H là các hằng số được tính từ giá trị R như sau: 52 1 1 1 2 2 22 2 222 33 11 1 1 1 2 2 22 2 211 33 22 1 1 1 2 2 22 2 211 22 33 F R R R G R R R H R R R = + − = + − = + − (2.47) Khi đó 11R , 22R , 33R , 12R , 13R và 23R là tỷ số dị hướng. Đối với trường hợp ứng suất phẳng, chỉ cần bốn tỷ số ứng suất. Ở đây, giả định rằng hướng cán (RD) là ứng suất tham chiếu do người dùng xác định nghĩa, khi đó 11R =1 và 22R , 33R tương ứng 1.0143, 1.2026 được tính toán theo hệ phương trình (2.48). ( 1)90 0 22 ( 1)0 90 ( 1)90 0 33 ( )0 90 r r R r r r r R r r + = + + = + (2.48) Để xây dựng FLC cho thép SPCC một cách đơn giản, một phương pháp đồ họa đã được sử dụng trong nghiên cứu này. Giai đoạn biến dạng phẳng được chọn đầu tiên và được thay thế vào phương trình (2.45): ' 1 ( 0) ( ) H khi H g = . Ở bất kỳ giai đoạn biến dạng nào thì phương trình (2.45) có thể được viết lại dưới dạng biểu thức (2.48). 'H B A H − (2.49) Khi đó 1/ ( )A g = (2.50) ( '/ ) ( / ')B f f = (2.51) ( )A và ( )B có thể xác định được từ hàm ứng suất Hill’s 1948 bằng cách áp dụng phương trình (2.46) đến các phương trình (2.48) - (2.50). Các kết quả cũng được trình bày trong các phương trình (2.52) - (2.58), Bảng 2.6 và Hình 2.13. 2( ) ( ) 2 ( )f G H H F H = + − + + (2.52) [ ( ) ] '( ) 2( ) 2 ( ) H F H f G H H F H − + + = + − + + (2.53) 53 ( ) ( ) ( ) F H H H G H + − = − + + (2.54) 2( )( ) '( ) 2[ ( )] F H G H H H G H + + − − + + (2.55) 2( ) 2 ( ) ( ) ( ) G H H F H g H G H + − + + = − + + (2.56) Khi đó: ( ) ( ) 2( ) 2 ( ) H G H A G H H F H − + + = + − + + (2.57) ( ) [( ) ] [ ( )] ( ) 2 2( ) 2 ( ) ( )( ) H F H F H H H G H B G H H F H F H G H H − + + + − − + + = + − + + + + − (2.58) Tính toán cho các chế độ biến dạng đặc biệt như biến dạng phẳng (P.S) ( 0 = ), biến dạng kéo đơn trục (U.T) ( 1/ 2 = − ) và biến dạng kéo đều đồng thời theo hai phương (B.T) ( 1 = ) có thể được lấy như liệt kê trong Bảng 2.6 cho A và B trong các phương trình. (2.57) và (2.58). Dựa trên các giá trị được tính toán và các phương trình đã nói ở trên, phương trình. (2.45) có thể được vẽ như thể hiện trong Hình 2.14 bằng cách áp dụng các mô hình Swift, Voce, Kim-Tuan. Bảng 2. 6 Các hệ số được xác định ở ba chế độ tạo hình, dựa trên hàm ứng suất Hill’s 1948 Phương pháp họa đồ như Hình 2.14 cho thấy giao điểm biến dạng phá hủy tương đương của các đường biến dạng (U.T), (P.S), (B.T) với các đường cong được xây dựng như dựa trên mô hình của Swift, Voce, Kim-Tuan được thể hiện như Bảng 2.7. Sau đó, các biến dạng chính và phụ được xác định thông qua các phương trình (2.59) - (2.61). FLC thu được bằng cách vẽ từ ba điểm biến dạng đặc biệt như trong Bảng 2.8 và đồ thị Hình.2.15. Chế độ (U.T) (P.S) (B.T) Hill 1948 𝛼 0 0,5 1 𝛽 -0,5 0 1 𝐴(𝛼) 1 0,882 0,439 𝐵(𝛼) 0,791 0 0,091 54 Bảng 2. 7 Biến dạng phá hủy tương đương với các mô hình vật liệu Hình 2. 14 Phương pháp hoạ đồ để đự đoán đường cong giới hạn tạo hình của kim loại tấm SPCC. Bảng 2. 8 Biến dạng chính – phụ với các mô hình vật liệu 1 2 2/ 1 1 12 1 R Rm m RR mm + = + + ++ (2.59) 2 1 = (2.60) 1 ( 2 ) 0 45 904 R r r r m = + + (2.61) Chế độ tạo hình Biến dạng tương đương (U.T) (P.S) (B.T) Voce 𝜀 ̅ 0,46 0,285 0,54 Swift 𝜀 ̅ 0,65 0,35 0,95 Kim-Tuan 𝜀 ̅ 0,68 0,37 1,06 Chế độ tạo hình (U.T) (P.S) (B.T) Voce 𝜀1 0,452 0,217 0,227 𝜀2 -0,226 0 0,227 Swift 𝜀1 0,638 0,267 0,399 𝜀2 -0,319 0 0,399 Kim-Tuan 𝜀1 0,668 0,282 0,445 𝜀2 -0,334 0 0,445 55 Trong đó 𝜀1, 𝜀2 tương ứng với các biến dạng chính và phụ, 𝜀 ̅là biến dạng tương đương, 𝛽 là tỷ lệ biến dạng, 𝑅𝑚 là giá trị Lankford. Hình 2. 15 FLC được tính toán dựa trên phương pháp họa đồ cho vật liệu tấm SPCC. Đường cong giới hạn tạo hình (FLC) được xây dựng như Hình 2.15 cho thấy FLC được xây dựng dựa trên mô hình của Voce thì các biến dạng chính và phụ tại các vị trí biến dạng phẳng (P.S), biến dạng kéo đơn trục (U.T) và biến dạng kéo đều đồng thời theo hai phương (B.T) là nhỏ nhất, tiếp đến là FLC được xây dựng theo mô hình của Swift và lớn nhất là FLC được xây dựng dựa trên mô hình của Kim- Tuan. Điều này chỉ ra rằng khi các FLC được dùng là một đầu vào trong mô phỏng số thì FLC được xây dựng dựa trên mô hình của Kim-Tuan cho biến dạng của vật liệu là lớn nhất. Tuy nhiên để đảm bảo độ chính xác của FLC theo dự đoán thì cần phải kiểm chứng với dữ liệu FLC thực nghiệm với vật liệu tương ứng. Trong các nghiên cứu trước đó của nghiên cứu sinh, về xây dựng FLC bằng phương pháp họa đồ dựa trên các mô hình vật liệu khác nhau được áp dụng với vật liệu tấm DP590 và vật liệu tấm 22MnB5 cho thấy rằng, khi sử dụng mô hình vật liệu của Voce cho kết quả FLC thấp hơn nhiều với dữ liệu FLD thực nghiệm với vật liệu tương ứng, còn khi sử dụng mô hình của Swift thấp hơn với dữ liệu FLD thực nghiệm. Trong khi đó khi sử dụng mô hình của Kim-Tuan cho dự đoán FLC tốt nhất với FLD thực nghiệm. Chính vì vậy trong nghiên cứu này mô hình của Kim-Tuan được dùng để xây dựng FLC của vật liệu SPCC tại các nhiệt độ khác nhau. 2.2.2 Xây dựng FLC của vật liệu tấm SPCC tại nhiệt độ khác nhau 2.2.2.1 Mối quan hệ giữa chỉ số ứng suất theo 3 phương, biến dạng tương đương và tỷ số biến dạng bằng mô hình phần tử hữu hạn (FE) Phần mềm thương mại ABAQUS 6.13 [83] đã được sử dụng trong nghiên cứu này để mô phỏng theo mô hình chày dập kéo dài Hecker’s [14]. Dữ liệu FLC được xây dựng dựa trên mô hình Kim-Tuan như Hình 2.15, sử dụng làm điều kiện biên trong quá trình mô phỏng FE. Kích thước của các mẫu và mô hình FE tương ứng được mô tả trong Hình 56 2.16 và Hình 2.17. Cụ thể, lưới được chia cho loại phần tử giảm tích hợp (S4R) được sử dụng cho phôi. Các bộ phận cối / chày và tấm chặn phôi được gán là cứng tuyệt đối. Kích thước của phần tử cho tất cả phôi tương ứng với khoảng 1 × 1 mm (chiều dài × chiều rộng). Hình 2. 16 Kích thước của mẫu thử FLD của vật liệu SPCC. Hình 2. 17 Mô hình phần tử hữu hạn dùng trong mô phỏng trong ABAQUS. Kết quả mô phỏng cho thấy vết rách có xu hướng xảy ra ở ứng suất kéo và biến dạng dẻo cao do lực kẹp lớn. Dựa trên các tiêu chí phá hủy, các giá trị dự đoán FLD đã bị thay đổi. Trong FE mô phỏng quá trình tạo hình, phá hủy xảy ra khi giá trị tiêu chí phá hủy đạt tới 1.0 và sau đó phần tử bị xóa. Hình 2.18 là kết quả mô phỏng FE khi sử dụng phương pháp họa đồ dùng để dự đoán đường cong giới hạn tạo hình. Hình 2. 18 Kết quả mô phỏng FE khi sử dụng phương pháp họa đồ để dự đoán FLC 57 Hình 2. 19 Mối quan hệ giữa chỉ số ứng suất theo 3 phương với biến dạng tương đương Hình 2. 20 So sánh giới hạn tạo hình của mô hình Hecker’s và dự đoán FLC bằng phương pháp họa đồ Từ các kết quả mô phỏng như trong Hình 2.18, một biểu đồ mô tả mối quan hệ giữa biến dạng tương đương ( f ) và chỉ số ứng suất theo 3 phương () như Hình 2.19, FLD như Hình 2.20 được xây dựng từ các biến dạng chính, biến dạng phụ của bốn mẫu (1stWP, 2ndWP, 3rdWP và 4thWP) và cho sự tương đồng với FLC được dự đoán bằng phương pháp họa đồ. Các tỷ lệ biến dạng () của bốn mẫu Hình 2.17, được tính bằng Phương trình 2.59 trong khi đó biến dạng chính ( 1 ) và biến dạng phụ ( 2 ) được xác định bởi dữ liệu trong Hình 2.20. 58 Bảng 2. 9 Biến dạng tương đương và chỉ số ứng suất theo 3 phương. Mẫu f (240C) 𝜼 1st WP 0,632 0,474 2nd WP 0,464 0,510 3rd WP 0,484 0,605 4th WP 0,653 0,652 Bảng 2. 10 Biểu thị chỉ số ứng suất theo 3 phương và tỷ số biến dạng. Mẫu 𝜼 1st WP 0,440 -0,481 2nd WP 0,510 -0,367 3rd WP 0,610 0,269 4th WP 0,665 0,616 Các hàm toán học giữa biến dạng tương đương ( f ) và chỉ số ưng suất theo ba phương () dựa theo mô hình void như Phương trình (2.61) (2.62), trình bày mối quan hệ giữa chỉ số ứng suất theo 3 phương () và biến dạng tương đương ( ductile f ). Từ dữ liệu trong Bảng 2.9, các hệ số của Phương trình (2.61) được xác định trong Bảng 2.11 và biểu đồ về mối quan hệ giữa biến dạng tương đương ( ductile f ) và bộ ba ứng suất () được xây dựng như trong Hình 2.22. Ngoài ra, các hệ số của Phương trình (2.61) được xác định như trong dữ liệu dựa trên Bảng 2.9, Bảng 2.10 và biểu đồ về mối quan hệ giữa chỉ số ứng suất theo 3 phương () và tỷ lệ biến dạng () được xây dựng như trong Hình 2.21. Từ Phương trình (2.61) và Phương trình (2.62), với bất kỳ một giá trị j nào trong phạm vi từ -0,5 đến 1 sẽ xác định một giá trị j tương ứng. Khi đó j và j lần lượt là tỷ lệ biến dạng và biến dạng tương đương tại điểm
File đính kèm:
 luan_an_nghien_cuu_anh_huong_cua_cac_thong_so_cong_nghe_va_n.pdf
luan_an_nghien_cuu_anh_huong_cua_cac_thong_so_cong_nghe_va_n.pdf 2. LATS - Luyen The Thanh -Tom tat (2022)- TV.pdf
2. LATS - Luyen The Thanh -Tom tat (2022)- TV.pdf 3. LATS - Luyen The Thanh -Tom tat-(2022)-TA.pdf
3. LATS - Luyen The Thanh -Tom tat-(2022)-TA.pdf 4. LATS Luyen The Thanh_thongtindonggopmoi_TV(2022).pdf
4. LATS Luyen The Thanh_thongtindonggopmoi_TV(2022).pdf 5. LATS Luyen The Thanh_thongtindonggopmoi_TA(2022).pdf
5. LATS Luyen The Thanh_thongtindonggopmoi_TA(2022).pdf Công văn đề nghị đang tải luận án lên hệ thống lên hệ thống dữ liệu quốc gia_Luyện Thế Thạnh.pdf
Công văn đề nghị đang tải luận án lên hệ thống lên hệ thống dữ liệu quốc gia_Luyện Thế Thạnh.pdf Quyết định thành lập hội đồng Bảo vệ cấp trường NCS_Luyện Thế Thạnh.pdf
Quyết định thành lập hội đồng Bảo vệ cấp trường NCS_Luyện Thế Thạnh.pdf

