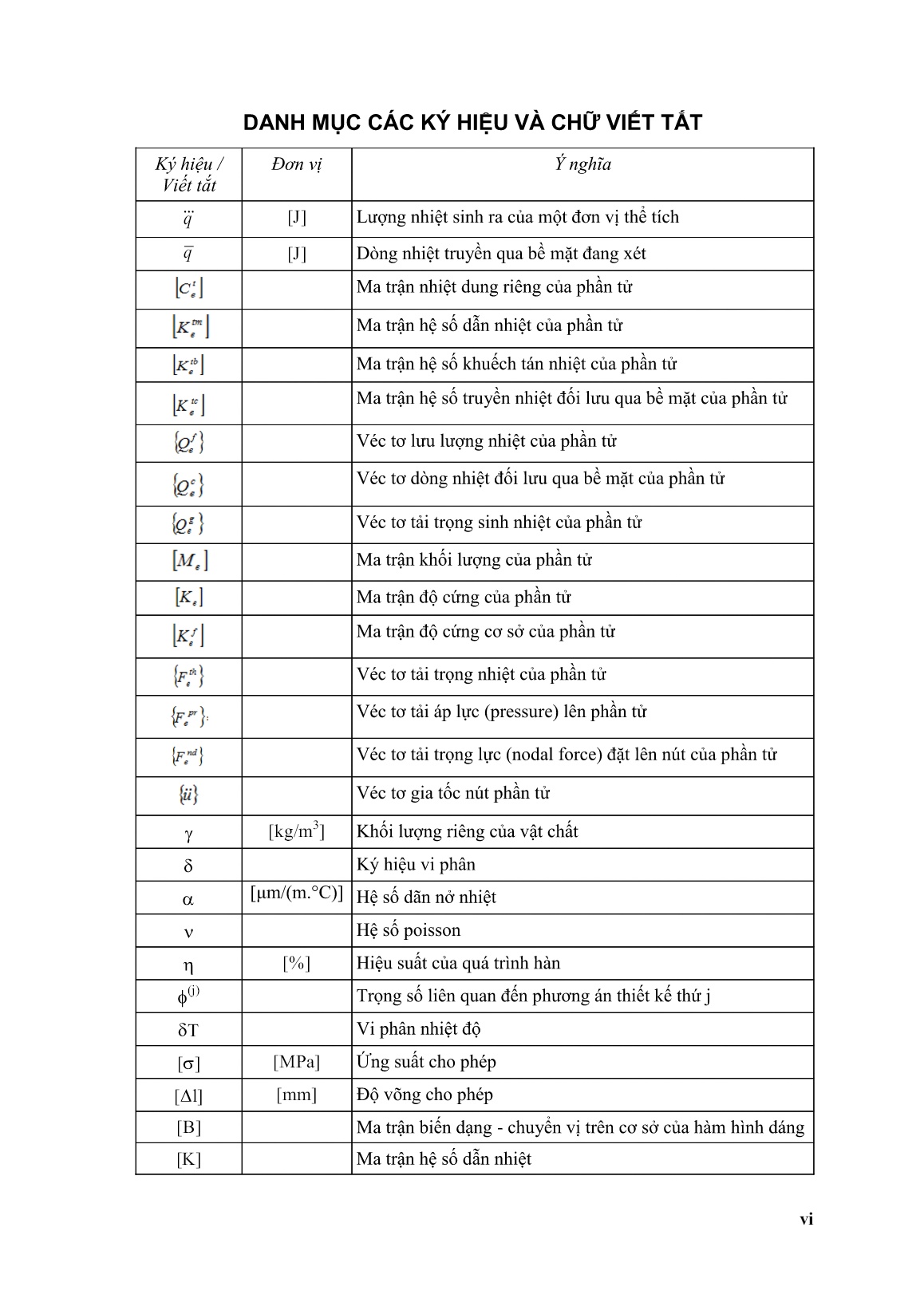
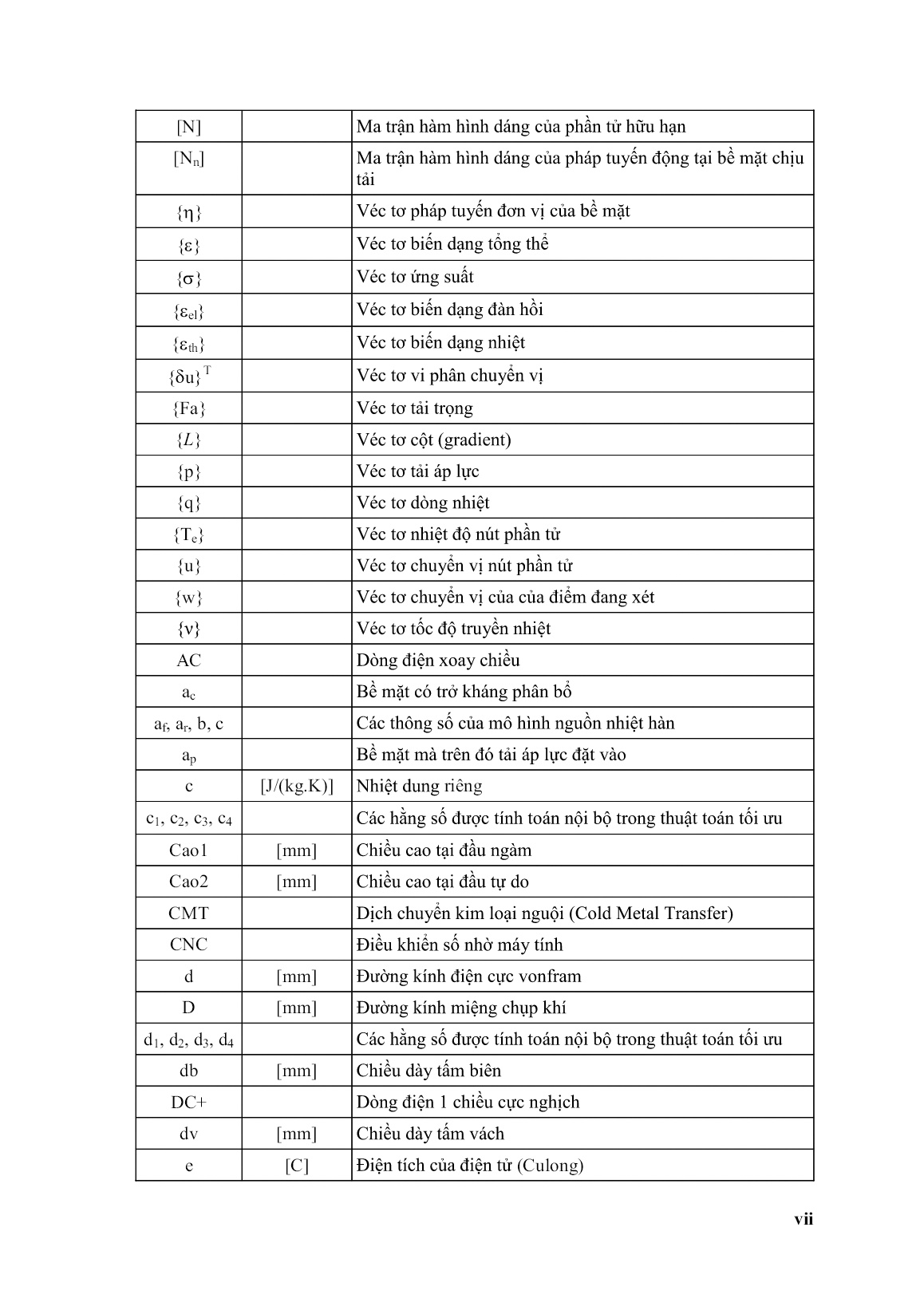
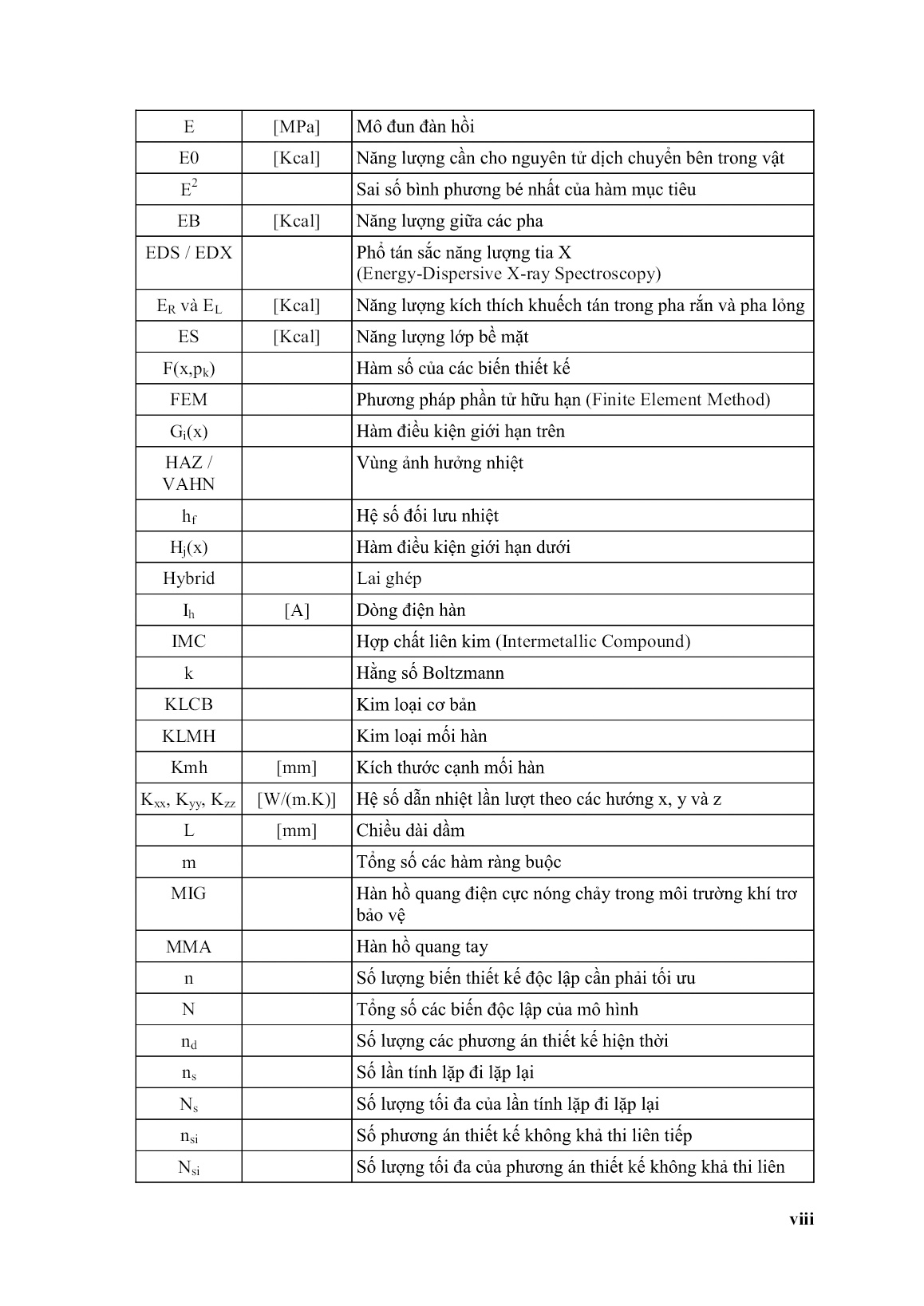
Luận án Nghiên cứu công nghệ hàn liên kết nhôm - Thép bằng quá trình hàn tig

như ảnh hưởng của các yếu tố công nghệ đến việc hình thành liên 
kết hàn hybrid nhôm – thép, thông qua đó đã đề ra được các biện pháp kỹ thuật thích hợp 
sử dụng trong quá trình hàn thử nghiệm ở chương 4. 
 Từ những nghiên cứu ở trên, có thể tóm lại rằng để hàn thành công nhôm với thép như 
đề tài luận án đề cập, cần phối hợp và thực hiện triệt để 3 nhóm giải pháp kỹ thuật sau 
đây: 
 Giải pháp về vật liệu: Chọn vật liệu hàn có thành phần hợp kim cao, vượt ra ngoài 
vùng nhạy cảm với nứt (chọn dây hàn ER4043 – hệ hợp kim Al-Si có chứa 5%Si). 
 Giải pháp về kết cấu: Vát mép tấm thép ở góc độ phù hợp để tạo khả năng chảy loang 
tốt của KLMH lên trên bề mặt của tấm thép. Tạo độ nhẵn và sạch triệt để bề mặt tấm thép, 
trong quá trình hàn cần tránh hiện tượng ôxi hoá để nhằm mục đích giảm mức năng lượng 
hoạt hóa, cải thiện tính thấm ướt và tạo độ ổn định cho quá trình tiếp xúc giữa hai kim loại 
lỏng và rắn. Kẹp chặt chi tiết hàn bằng đồ gá và bảo đảm đúng kích thước khe hở hàn. 
 Giải pháp về công nghệ: Sử dụng quá trình hàn ít hydro (TIG). Sử dụng hiệu ứng bắn 
phá catot bằng dòng hàn AC hoặc DC+. Làm sạch dầu mỡ bảo quản trên phôi, đặc biệt là 
làm sạch triệt để mép hàn khỏi các lớp gỉ, bụi bẩn, bằng phương pháp cơ học (bàn chải 
có sợi thép không gỉ, giấy ráp). Trong trường hợp này không dùng thuốc hàn vì phức tạp 
trong khâu xử lý thuốc dư. Không sử dụng lớp phủ trung gian (Al hoặc Zn) vì các bất lợi 
như đã phân tích ở phần tổng quan. Sử dụng năng lượng đường thấp, khống chế vũng hàn 
nhỏ, hàn ở tốc độ cao. Kiểm soát chặt chẽ chu trình nhiệt hàn (nhiệt độ và thời gian 
khuếch tán kim loại). Để hồ quang tập trung và tránh bị thổi lệch khi hàn bằng cách mài 
đầu điện cực vonfram ở dạng nón cụt thay vì mài tròn như hàn nhôm thông thường. 
 Ba nhóm giải pháp này sẽ là cơ sở khoa học quan trọng áp dụng trong quá trình nghiên 
cứu thực nghiệm ở chương 4 nhằm tạo ra được liên kết hàn hybrid nhôm – thép như đối 
tượng nghiên cứu đã nêu trong phần mở đầu. 
 39 
3. MÔ PHỎNG SỐ XÁC ĐỊNH CHẾ ĐỘ CÔNG NGHỆ HÀN TIG LIÊN 
 KẾT HYBRID NHÔM - THÉP DẠNG CHỮ T 
 Liên kết hàn hybrid nhôm – thép như đã mô tả là một bài toán mới, nên nếu chỉ tiến 
hành nghiên cứu thực nghiệm đơn thuần thì sẽ mất rất nhiều thời gian và đặc biệt là chi phí 
thực nghiệm. Số lượng thí nghiệm có thể phải lên tới hàng trăm, thậm chí tới hàng ngàn, 
gây ra một sự tốn kém và lãng phí lớn. 
 Ưu thế của máy tính điện tử và khoa học mô phỏng là lợi ích biết và dự đoán trước được 
các sự kiện sẽ xảy ra trong thực nghiệm, từ đó giúp chúng ta tìm ra được dải thông số công 
nghệ thích hợp nhất để áp dụng trong thực nghiệm, giúp cho quá trình thực nghiệm nhanh 
hội tụ đến đích và giảm được nhiều chi phí do không phải thực nghiệm ở vùng thông số 
không thích hợp. Trên cơ sở đó tác giả sử dụng phương pháp nghiên cứu mô phỏng số quá 
trình hàn TIG cho liên kết hybrid nhôm – thép trước khi tiến hành nghiên cứu thực nghiệm. 
3.1. Mục đích 
 Các kết quả nghiên cứu trong chương 2 đã đưa ra nhận định rằng nhiệt độ và thời gian 
khuếch tán kim loại là hai thông số cốt lõi quyết định đến quá trình hình thành liên kết hàn 
hybrid nhôm – thép, do vậy chương này sẽ tìm cách chứng minh nhận định đó thông qua 
đề xuất mô hình tính toán và mô phỏng quá trình hàn TIG liên kết hàn hybrid nhôm – thép 
đã nêu để đưa ra các dự báo trước về trường nhiệt, chu trình nhiệt và thời gian khuếch tán 
kim loại, đồng thời kết hợp với các kết quả nghiên cứu ở chương 2 sẽ tìm ra được dải 
chế độ công nghệ hàn phù hợp cho quá trình thực nghiệm ở chương 4. 
 Nghiên cứu mô phỏng còn nhằm mục đích nắm bắt quá trình hàn một cách tổng quát và 
trực quan, giảm nhiều các chi phí thử nghiệm do tránh được việc thực nghiệm ở các vùng 
thông số không thích hợp. 
3.2. Cơ sở lý thuyết và phương pháp nghiên cứu 
3.2.1. Số hóa phương trình truyền nhiệt khi hàn 
 Trong hàn nóng chảy nói chung và hàn hồ quang nói riêng, quá trình truyền nhiệt trong 
vật hàn là nguyên nhân của các vấn đề phát sinh trong đó (gồm các quá trình: nóng chảy, 
biến đổi tổ chức, khuếch tán, tiết pha mới, gây ra ứng suất, biến dạng,). Mặt khác, theo 
các kết quả nghiên cứu ở chương 2 thì các thông số quan trọng quyết định đến khả năng 
hình thành liên kết hàn giữa KLMH và tấm thép CCT38 bao gồm độ sạch và nhẵn của bề 
mặt tấm thép, nhiệt độ và thời gian khuếch tán kim loại. Trong đó nhiệt độ và thời gian 
khuếch tán kim loại là hai thông số quyết định nhất, do vậy chúng ta cần phải nghiên cứu 
về quy luật phân bố của trường nhiệt hàn trong liên kết hàn nghiên cứu. 
 Cơ sở của nghiên cứu quá trình truyền nhiệt xuất phát từ định luật thứ nhất của nhiệt 
động lực học. Định luật này phát biểu rằng: năng lượng nhiệt được bảo tồn và được mô tả 
bởi phương trình vi phân như sau [49]: 
  ∂T T  T
 γ .c + {v} {L}T  + {L} {q}= q (3.1) 
  ∂t 
Ở đây: γ là khối lượng riêng của vật chất, c là nhiệt dung riêng, T là nhiệt độ (=T(x,y,z,t)) 
 T
  ∂ ∂ ∂ 
 {L}=  , ,  T
 ∂ ∂ ∂ {v} = {v ,v ,v }
và t là biến thời gian. Ta ký hiệu:  x y z  là véc tơ cột (gradient), x y z là 
 
véc tơ tốc độ truyền nhiệt, {q} là véc tơ dòng nhiệt và q là lượng nhiệt sinh ra của một 
đơn vị thể tích. 
 Theo định luật Fourier [49], quan hệ giữa véc tơ dòng nhiệt và gradient nhiệt độ là: 
 {q}= −[K]{L}T (3.2) 
 40 
 K xx 0 0 
 =  
 [K]  0 K yy 0 
  
  0 0 K zz 
 Với , trong đó Kxx, Kyy, Kzz là các hệ số dẫn nhiệt lần lượt theo các 
hướng x, y và z 
 Kết hợp các phương trình (3.1) và (3.2) ta được phương trình sau: 
  ∂T T  T
 γ .c + {v} {L}T  = {L} ([K]{L}T ) + q (3.3) 
  ∂t 
Đối với bài toán truyền nhiệt, chúng ta có 3 điều kiện biên như sau [48]: 
 a) Nhiệt độ xác định trên bề mặt S1: 
 T = T (3.4) 
 b) Dòng nhiệt truyền qua bề mặt xem xét S2 (dẫn nhiệt): 
 T
 q = −{q} {η} (3.5) 
 q
 Với {η} là véc tơ pháp tuyến đơn vị của bề mặt S2 và là dòng nhiệt truyền qua bề 
 mặt S2 đang xét. 
 c) Lượng nhiệt đối lưu và bức xạ qua bề mặt S3 (theo định luật làm mát Newton): 
 T
 {q} {η}= h f (T −TB )
 (3.6) 
 Với hf là hệ số đối lưu nhiệt, TB là nhiệt độ của môi trường và T là nhiệt độ trên bề 
 mặt của mô hình. 
Chú ý rằng: dòng nhiệt mang dấu dương là dòng nhiệt đi vào trong mô hình (ngược hướng 
với véc tơ pháp tuyến đơn vị của bề mặt đang xét {η}). 
Kết hợp phương trình (3.2) với (3.5) và (3.6) ta được: 
 η T =
 { } [K]{L}T q (3.7) 
 {η}T [K]{L}T = h (T −T )
và f B (3.8) 
 Nhân phương trình (3.3) với vi phân nhiệt độ δT, rồi tích phân qua thể tích phần tử Ve, 
và kết hợp với các phương trình (3.7) và (3.8) ta được: 
   ∂T T  T 
 γ .c.δT + {v} {L}T  + {L} (δT )([K]{L}T )dV = δT.q.dS 2 + δT.h f .(TB − T )dS3 + δT.q.dVe (3.9) 
 ∫   e ∫S ∫S ∫V
 Ve   ∂t   2 3 e
3.2.2. Xây dựng ma trận dòng nhiệt 
 Theo lý thuyết phần tử hữu hạn [50], nhiệt độ được xác định bởi công thức: 
 T = [N]T {T }
 e (3.10) 
Với: [N]=[N(x,y,z)] là ma trận hàm hình dáng về nhiệt độ của phần tử, còn {Te}={Te(t)} là 
véc tơ nhiệt độ nút của phần tử. Từ đó suy ra: 
  ∂T T 
 T = = [N] {Te }
 ∂t (3.11) 
 δT = {δT }T [N]
và e (3.12) 
 = T {L}T = [B]{T }
Ta ký hiệu ma trận: [B] {L}[N] khi đó thì: e (3.13) 
Kết hợp các phương trình (3.9), (3.10), (3.11), (3.12) và (3.13) ta được: 
 γ δ T T  + γ δ T T +
∫ .c{ Te } [N][N] {Te }dVe ∫ .c{ Te } [N]{v} [B]{Te }dVe
 Ve Ve
 T T T
 δ T T = {δT } [N].q.dS + {δT } [N].h . T − [N] {T }dS
∫ { Te } [B] [K][B]{Te }dVe ∫ e 2 ∫ e f ( B e ) 3
 Ve S2 S3
+ δ T 
 ∫ { Te } [N].q.dVe
 Ve (3.14) 
Rút gọn phương trình (3.14) và đưa các hằng số ra ngoài dấu tích phân ta được: 
 41 
 T T
γ c.[N][N] dV {T }+ γ c.[N]{v} [B]dV {T } + γ T = 
 ∫ e e ∫ e e ∫ [B] [K][B]dVe {Te }
 Ve Ve Ve
 + − [ ][ ]T { } + [ ]
∫ [N].q.dS 2 ∫ TB .h f .[N]dS 3 ∫ hf . N N Te dS3 ∫ q. N dVe
 S2 S3 S3 Ve (3.15) 
Viết gọn phương trình (3.15) dưới dạng ma trận, ta được: 
C t T + K tm + K tb + K tc {T }= Q f + Qc + Q g
[ e ]{ e } ([ e ] [ e ] [ e ]) e ({ e } { e } { e }) (3.16) 
Trong đó: 
 t = γ T
[Ce ] ∫ c[N][N] dVe là ma trận nhiệt dung riêng của phần tử 
 Ve
 tm = γ T
[K e ] ∫ c[N]{v} [B]dVe là ma trận hệ số dẫn nhiệt của phần tử 
 Ve
 tb = T
[K e ] ∫ [B] [K][B]dVe
 Ve là ma trận hệ số khuếch tán nhiệt của phần tử 
 tc = T
[K e ] ∫ h f .[N][N] dS3
 S3 là ma trận hệ số truyền nhiệt đối lưu qua bề mặt của phần tử 
 f =
{Qe } ∫ [N].q.dS2
 S2 là véc tơ lưu lượng nhiệt của phần tử 
 c =
{Qe } ∫ TB .h f .[N]dS3
 S3 là véc tơ dòng nhiệt đối lưu qua bề mặt của phần tử 
 g = 
{Qe } ∫ q.[N]dVe
 Ve là véc tơ tải trọng sinh nhiệt của phần tử 
3.2.3. Xây dựng ma trận kết cấu 
 Muốn nghiên cứu cả ứng xử của vật liệu về mặt cơ học (đặc trưng bởi ứng suất, biến 
dạng,...), chúng ta cần phải đưa các lý thuyết về cơ học vào trong mô hình nghiên cứu. 
Nghĩa là chúng ta cần phải tiến hành giải một bài toán hỗn hợp đa trường nhiệt – kết cấu. 
 Theo nguyên lý chuyển vị khả dĩ thì ta có quan hệ giữa công khả dĩ và công do ngoại 
lực tạo ra là [51]: 
 δU = δV (3.17) 
Ở đây: U là công khả dĩ do nội lực gây ra (U=U1+U2) và V là công do ngoại lực tạo ra 
(V=V1+V2+V3) và δ là ký hiệu vi phân. 
 Thành phần thứ nhất của công khả dĩ (U1) được xác định bởi công thức sau [52]: 
 T
 δU1 = {δε}{σ}d(Ve )
 ∫V
 e (3.18) 
Trong đó: {ε} là véc tơ biến dạng tổng thể, {σ} là véc tơ ứng suất và Ve là thể tích của 
phần tử khảo sát. 
Nếu gọi [D] là ma trận độ cứng thì: {σ} = [D]{εel} hay {σ} = [D]({ε}-{εth}) (3.19) 
Với: {εel} là véc tơ biến dạng đàn hồi và {εth} là véc tơ biến dạng nhiệt. 
Kết hợp các phương trình (3.19) và (3.18) ta được: 
 δ = δε T ε − δε T ε th
 U1 ∫ ({ } [D]{ } { } [D]{ })dVe
 Ve (3.20) 
 Gọi [B] là ma trận biến dạng - chuyển vị trên cơ sở của hàm hình dáng của phần tử hữu 
hạn (PTHH) và {u} là véc tơ chuyển vị nút phần tử, ta sẽ có: 
 ε =
 { } [B]{u} (3.21) 
 Thay (3.21) vào (3.20) ta được: 
 T T T T th
δU1 = {δu} [B] [D][B]dVe {u}− {δu} [B] [D]{ε }dV
 ∫V ∫ e
 e Ve (3.22) 
 42 
 Thành phần thứ 2 của công khả dĩ (U2) được xác định khi một bề mặt dịch chuyển 
chống lại một trở kháng phân bổ như là một độ cứng cơ sở, nó được mô tả bởi công thức 
[52]: 
δ = δ T σ
 U 2 ∫ { wn } { }da f (3.23) 
 ac
Ở đây: wn là pháp tuyến động của bề mặt, {σ} là véc tơ ứng suất trên bề mặt, ac là bề mặt 
có trở kháng phân bổ. 
 Chúng ta biết rằng quan hệ giữa véc tơ chuyển vị nút của phần tử và pháp tuyến động 
của bề mặt trở kháng phân bổ được thể hiện qua công thức: 
 {wn }= [N n ]{u}
 (3.24) 
Với: [Nn] là ma trận hàm hình dáng của pháp tuyến động tại bề mặt chịu tải. 
 Ứng suất {σ} được biểu diễn bởi công thức: 
 {σ}= k.{w }
 n (3.25) 
Với: k là độ cứng cơ sở đơn vị của lực trên chiều dài và trên đơn vị diện tích bề mặt. 
 Kết hợp các công thức (3.23), (3.24), (3.25) và đưa hằng số k ra khỏi dấu tích phân, ta 
được: 
 δ = δ T T
 U 2 { u} .k.∫ [N n ] [N n ]da f .{u}
 a f
 (3.26) 
 Thành phần thứ nhất của công do ngoại lực tác động (V1) được xem xét dựa vào hiệu 
ứng quán tính [52]: 
 a
 T {F }
 δ = − δ
 V1 ∫ { w} dVe
 Ve
 Ve (3.27) 
Ở đây: {w} là véc tơ chuyển vị của của điểm đang xét, {Fa} là véc tơ tải trọng (theo 
D’Alembert). Theo theo định luật 2 của Newton, ta có: 
 {F a } ∂ 2
 = γ
 2 {w} (3.28) 
 Ve ∂t
Ở đây: γ là khối lượng riêng của vật chất, t là biến thời gian. 
 Chuyển vị bên trong phần tử được liên hệ với chuyển vị nút theo công thức: 
 =
 {w} [N]{u} (3.29) 
Với: [N] là ma trận hàm hình dáng của phần tử. 
Kết hợp các công thức (3.27), (3.28), (3.29) và đưa hằng số γ ra ngoài dấu tích phân, ta 
được: 
 2
 T T ∂
 δ = −{δ } γ [ ] [ ] { } (3.30) 
 V1 u . .∫ N N dVe 2 u
 Ve ∂t
 Véc tơ tải trọng áp lực (pressure load vector) sẽ gây ra một công (V2) và được xác định 
bằng công thức [52]: 
 δ = δ T
 V2 ∫ { wn } {p}da p
 a p
 (3.31) 
Ở đây: {p} là véc tơ tải áp lực, còn ap là bề mặt mà trên đó tải áp lực đặt vào. 
 Kết hợp các công thức (3.29) và (3.31) ta được: 
 δ = δ T
 V2 { u} ∫ [N n ]{p}da p
 a p (3.32) 
Chú ý rằng: tải áp lực được đặt vào bề mặt ngoài của phần tử và cả trên đường bao của bề 
mặt ngoài đó. 
 nd
 {Fe }
 Lực nút (nodal force) tác dụng lên phần tử sẽ gây nên một công (V3), và được 
biểu diễn bằng công thức [52]: 
 43 
 δV = {δu}T F nd
 3 { e } (3.33) 
 Cuối cùng, tổng hợp các phương trình (3.17), (3.22), (3.26), (3.30), (3.32) và (3.33) ta 
nhận được phương trình: 
 T T
 T T th
{δu} [B] [D][B]dVe {u}− {δu} [B] [D] ε dV +
 ∫V ∫ { } e
 e Ve
 δ T T = 2
{ u} .k.∫ [Nn ] [Nn ]da f {u} T T ∂
 a f − {δ } γ [ ] [ ] { }+
 u . .∫ N N dVe 2 u
 Ve ∂t
 δ T T + δ T nd
{ u} ∫ [N n ] {p}da p { u} {Fe } (3.34) 
 a p
 Chú ý rằng véc tơ vi phân chuyển vị {δu}T có giá trị bé tùy ý, và do nó có mặt trong 
toàn bộ các thành phần của phương trình (3.34) nên có thể được giản lược. Viết gọn 
phương trình (3.34) dưới dạng ma trận ta được: 
 [M ]{u}− [K ]+ K f {u}= th + pr + nd
 e ( e [ e ]) {F } {F } {F } (3.35) 
Ở đây: 
 = γ T
[M e ] ∫ [N] [N]dVe là ma trận khối lượng của phần tử 
 Ve
 = T
[K e ] ∫ [B] [D][B]dVe
 Ve là ma trận độ cứng của phần tử 
 f = T
[K e ] k∫ [N n ] [N n ]da f
 a f là ma trận độ cứng cơ sở của phần tử 
 th = T ε th
{Fe } ∫ [B] [D]{ }dVe
 Ve là véc tơ tải trọng nhiệt của phần tử 
 pr = T
{Fe } ∫ [N n ] {p}da p
 a p là véc tơ tải áp lực (pressure) lên phần tử 
 F nd
{ e } là véc tơ tải trọng lực (nodal force) đặt lên nút của phần tử 
 ∂ 2
  =
{u} 2 {u}
 ∂t là véc tơ gia tốc nút phần tử 
Biến dạng nhiệt trong liên kết hàn: 
 Trong trường hợp hệ số dãn nở nhiệt α là hàm số của nhiệt độ (α = α(T)), quan hệ giữa 
biến dạng nhiệt εth và α được biểu diễn như sau: 
 T
 ε th = ∫α(T ).dT
 T
 B (3.36) 
Trong đó: TB là nhiệt độ môi trường và T là nhiệt độ tức thời tại nút đang xét. α được xác 
định theo đặc tính truyền nhiệt của vật liệu nghiên cứu cụ thể. 
3.2.4. Thiết lập bài toán đa trường nhiệt – kết cấu 
 Trong quá trình tính toán mô phỏng bài toán hàn tổng quát, chúng ta không chỉ tính toán 
trường nhiệt mà còn phải quan tâm cả đến ứng suất và biến dạng do nguồn nhiệt hàn sinh 
ra. Để làm việc đó ta tiến hành tổ hợp các phương trình (3.16) và (3.35) với việc đưa thêm 
tham số ma trận suy giảm [C] trong trường hợp giải bài toán tổng quát (có tính đến tính 
dẻo của vật liệu) ta sẽ thu được hệ phương trình ma trận đầy đủ cho toàn bộ mô hình 
PTHH như sau [51]: 
 [M ] [0]{u} [C] [0] {u}
 + + [K] [0] {u} {F}
     t     =  
 [0] [0] T [0] C T  t  { } { }
  { }  [ ]{ }  [0] [K ] T   Q  (3.37) 
 44 
 3.3. Xác định kích thước của liên kết hàn hybrid nhôm – thép 
 dạng chữ T bằng phương pháp số 
 Do liên kết hàn hybrid nhôm – thép dạng chữ T đề cập trong luận án này là một bài toán 
 mới, bài toán phi tiêu chuẩn nên chưa có bất kỳ một tiêu chuẩn hay quy phạm ứng dụng 
 nào để có thể tra cứu, vì vậy việc tiến hành tính toán các kích thước của liên kết hàn này 
 nhằm mục đích trả lời các câu hỏi “kích thước liên kết hàn như vậy chịu được tải trọng bao 
 nhiêu?” và/hoặc “thiết kế như vậy đã hợp lý chưa?” là một nội dung cần thiết phải đề cập. 
 Mặt khác, nhằm mục đích đưa ra một giải pháp nghiên cứu có tính tương đối toàn diện 
 đối với bài toán mới từ khâu thiết kế đến khâu chế tạo, mà nội dung này trở thành một 
 phần nghiên cứu mở rộng nhưng quan trọng và nên được công bố. 
 3.3.1. Thiết kế liên kết hàn hybrid nhôm – thép bằng kỹ thuật tính toán tối ưu 
 3.3.1.1. Bài toán tối ưu trong thiết kế kết cấu: 
 Giả sử có n biến thiết kế độc lập cần phải tính toán tối ưu (ở đây chính là kích thước 
 hình học của các phần tử của kết cấu / liên kết hàn) được tập hợp dưới dạng một véc tơ x = 
 {x1, x2,, xn}, trong đó các biến xi nằm trong một phạm vi giữa các cận dưới và cận trên 
 (xi ≤ xi ≤ xi). Mục đích của ta là đưa hàm mục tiêu (trọng lượng hoặc thể tích của kết cấu) f 
 = f(x) min trong khi phải thỏa mãn đồng thời tất cả các điều kiện ràng buộc (hàm điều 
 kiện). Các� hàm điều kiện (Gi(x), Hj(x), Wk(x)) có thể ở một hoặc đồng thời trong các dạng 
 sau đây [51]: 
 Gi(x) ≤ gi với i = 1 ÷ m1 (loại hàm giới hạn trên) (3.38) 
 h ≤ H (x) với j = 1 ÷ m (loại hàm giới hạn dưới) (3.39) 
 j j � 2
 wk ≤ Wk(x) ≤ wk với k = 1 ÷ m3 (loại hàm giới hạn cả cận trên và cận dưới) (3.40) 
 Một phương án thiết kế được gọi là “khả thi” nếu như tồn tại một véc tơ x*={x1*, 
 �
 x2*,,xn*} mà thỏa mãn được đồng thời tất cả các hàm ràng buộc, nghĩa là: 
 gi* = Gi(x*) ≤ gi + αi (3.41) 
 h - β ≤ h * = H (x*) (3.42) 
 j j j �j
 wk - γk ≤ wk* = Wk(x*) ≤ wk + γk (3.43) 
 Trong đó α , β và γ là các sai số cho phép của các hàm điều kiện và m = m + m + m là 
 i j k � 1 2 3
 tổng số các hàm ràng buộc. 
 Một phương án thiết kế được gọi là “tối ưu” nếu như nó là phương án “khả thi” và tại 
 đó hàm mục tiêu đạt cực trị (trọng lượng hoặc thể tích của kết cấu đạt giá trị nhỏ nhất): 
 f* = min f(x) với xi ≤ xi* ≤ xi (3.44) 
 • Tối ưu hóa cục bộ và tối ưu hóa toàn phần: 
 �
 Gọi N là tổng số các biến độc lập của mô hình và n là số các biến cần tối ưu thì nếu n ≤ 
 N ta có bài toán tối ưu hóa cục bộ, còn nếu n = N thì ta có bài toán tối ưu hóa toàn phần. 
 • Ràng buộc cục bộ và ràng buộc tổng thể: 
 Nếu các hàm ràng buộc G(x), H(x) và W(x) lấy trên toàn bộ mô hình thì ta có ràng buộc 
 tổng thể, còn nếu lấy trên một phần của mô hình thì ta có ràng buộc cục bộ. 
 • Thuật toán tối ưu thiết kế kết cấu: 
 a) Các xấp xỉ hàm số: 
 Giả sử ký hiệu xấp xỉ của hàm số bằng dấu ^ thì xấp xỉ của hàm mục tiêu và của các 
 hàm ràng buộc được thể hiện như sau: 
 f(x) = f(x) + η (3.45) 
 ̂
 45 
 g(x) = g(x) + (3.46) 
 h(x) = h(x) + (3.47) 
 � α
 w(x) = w(x) + γ (3.48) 
 � β
 Theo tài liệu [51], hình thức phức tạp nhất của xấp xỉ sẽ có dạng: 
 �
 f = a + a x + b x x (3.49) 
 Một kỹ thuật bình phươngn bé nhấtn n của các trọng số sẽ được sử dụng để xác định các hệ 
 ̂ 0 ∑i i i ∑i ∑j ij i j
 số ai và bij trong phương trình (3.49), ví dụ sai số bình phương bé nhất của hàm mục tiêu 
 có dạng: 
 (3.50) 
 Ở đây: φ(j) là trọng số liên quan đến phương án thiết kế thứ j 
 nd là số lượng các phương án thiết kế hiện thời 
 Đối với các hàm ràng buộc cũng sẽ được suy diễn tương tự như dạng thức của E2 trong 
 phương trình (3.50). Các hệ số trong phương trình (3.50) được xác định bằng việc tối thiểu 
 hóa E2. Các trọng số được sử dụng ở trên được tính theo một trong các cách sau đây: 
 - Dựa trên các giá trị của hàm mục tiêu, các phương án thiết kế cho giá trị hàm mục 
 tiêu thấp sẽ có trọng số cao. 
 - Căn cứ vào giá trị của biến thiết kế, các phương án thiết kế gần gũi hơn với thiết kế 
 tốt nhất sẽ nhận được trọng số cao. 
 - Dựa trên tính khả thi, phương án khả thi có trọng số cao và phương án không khả thi 
 có trọng số thấp. 
 Một số lượng nhất định các phương án thiết kế phải tồn tại để hình thành các xấp xỉ, nếu 
 không thì các phương án thiết kế ngẫu nhiên sẽ được tạo ra cho đến khi thu được số lượng 
 yêu cầu. Điều này có thể được diễn tả như sau (với n là số lượng các biến thiết kế, nd là số 
 lượng các phương án thiết kế): 
 nd < n + 2: sinh ra các phương án thiết kế ngẫu nhiên (3.51) 
 nd ≥ n + 2: hình thành các xấp xỉ 
 Nếu như nhiều dữ liệu (các phương án thiết kế) được tạo ra thì các thành phần trong 
 phương trình (3.49) tăng lên và thời gian tính toán sẽ nhiều hơn. 
 b) Tối thiểu hóa các xấp xỉ hàm số: 
 Với các xấp xỉ hàm số có sẵn, vấn đề tối thiểu hóa các ràng buộc được viết lại như sau: 
 Tối thiểu hóa hàm số f=f(x) (3.52) 
 ≤ ≤ x
 Thỏa mãn các ràng buộc:̂ ̂ xi xi i (i=1,2,3,n) (3.53) 
 g (x) ≤ g + α (i=1,2,3,m ) (3.54) 
 i i� i 1
 h - β ≤ h (x) (i=1,2,3,m ) (3.55) 
 �i i � i 2
 γ ≤ w ≤ w γ
 wi - i � i(x) i + i (i=1,2,3,m3) (3.56) 
 Bước tiếp theo là chuyển đổi các phương trình (3.52) đến (3.56) từ vấn đề bị ràng buộc 
 thành không bị ràng buộc. Điều này �được thực� hiện bằng các “hàm phạt”, dẫn đến phát 
 biểu sau đây: Tối thiểu hóa hàm số 
 min (3.57) 
 46 
 Trong đó X là hàm phạt