Luận án Nghiên cứu dao động ô tô tải sản xuất lắp ráp ở Việt Nam khi vận chuyển gỗ trên đường lâm nghiệp

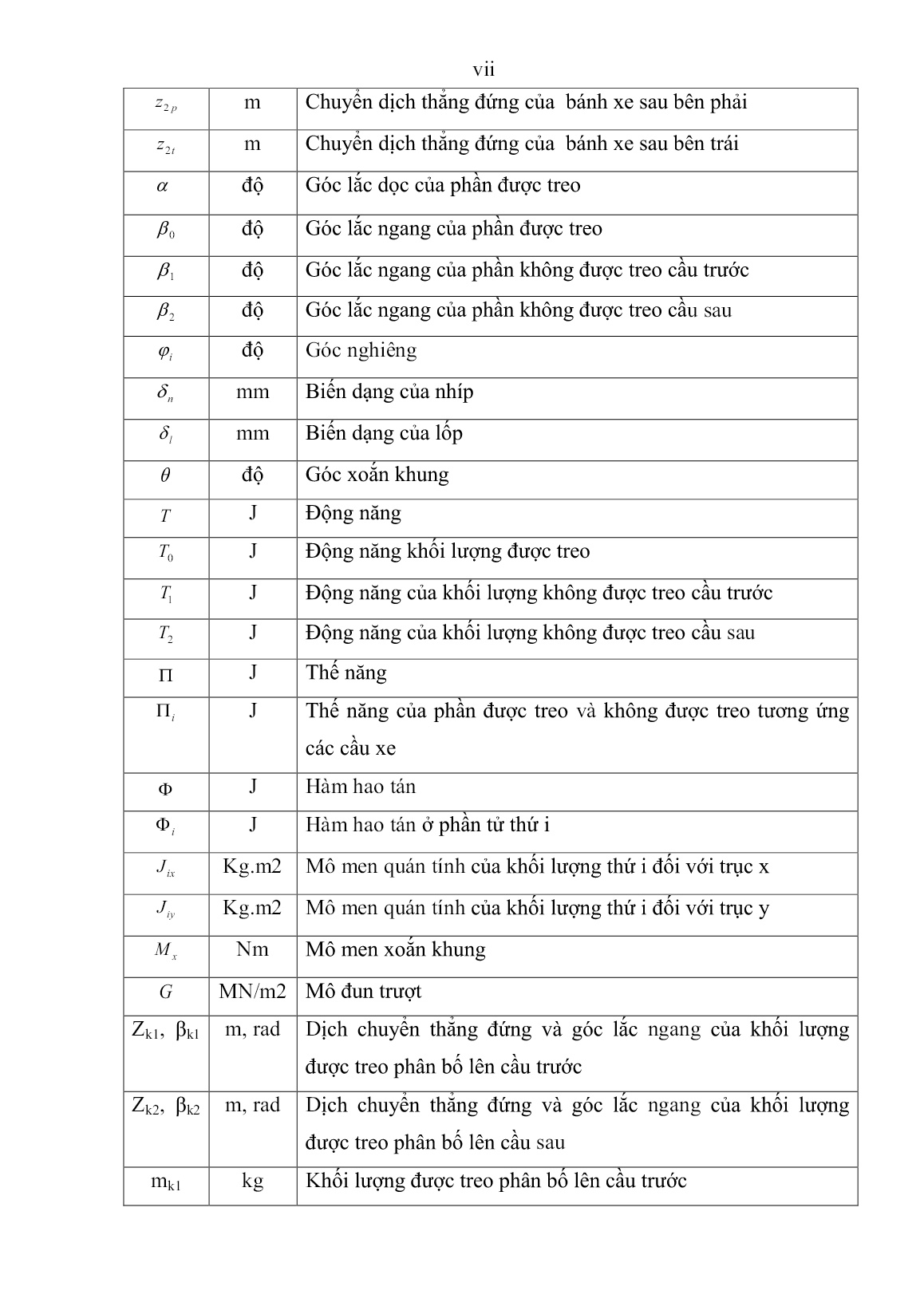
in βk2 = z0+l2.sinα0.cos βk2+bp sin βk2; 
z1t= z1 –bt sin β1 ; z1p= z1 +bt sin β1; 
z2t= z2 –bt sin β2 ; z2p= z2 +bt sin β2; 
 Dao động quanh vị trí cân bằng tĩnh với các dịch chuyển nhỏ, nên có thể 
coi gần đúng: Sinαi ≈ αi , cos αi ≈1 và sin βi ≈ βi , cos βi ≈1 (i=0, 1, 2). 
 Ngoài ra có thể xem bt = bp = b/2, ta có: 
zA= z0-l1.α0 ; zB= z0+l2.α0 zc= z0 - hc
zAt= z0-l1.α0 -
2
b
 βk1 , zBt= z0+l2.α0 -
2
b
 βk2 ; 
zAp= z0-l1.α0 +
2
b
 βk1 zBp= z0+l2.α0 +
2
b
 βk2 ; (2.1) 
zi t= zi +
2
b
.βi , zi p= zi -
2
b
.βi , (i = 1, 2) 
Các góc βk1 , βk2 có thể xác định theo β0 như sau: 
Khi phần được treo có khối lượng m0 bị lắc quanh trục dọc một góc β0 thì 
trọng tâm của phần được treo cũng sẽ lệch một góc β0 so với phương thẳng 
 42 
đứng. Khi đó thành phần của trọng lượng phần được treo P = m0g là Psin β0 sẽ 
gây ra mô men xoắn khung xe: 
MX = Psin β0.hC ≈ P. β0.hC (2.2) 
Trong đó, hC là khoảng cách theo phương thẳng đứng từ khối lượng phần 
được treo đến khung xe. 
 Nếu coi khung xe là vật biến dạng thì góc xoắn tương đối giữa hai mặt cắt 
A và B (hình 2.5) sẽ là: 
 θ = βk1 - βk2 
A C B
M
A
C
M
M
B
a a,
b,
c,
a) Biến dạng xoắn của khung b) Biểu đồ mô men xoắn 
Hình 2.5. Mô hình biến dạng của khung - sàn xe khi βk1 ≠ βk2 
 Trong đó các giá trị βk1 , βk2 xác định như sau: 
 Gọi mô men xoắn tại tiết diện C là MC, được xác định theo công thức 
(2.2), ta có sơ đồ phân bố mô men xoắn theo chiều dài khung xe như hình 2.5b, 
đây là hệ siêu tĩnh bậc 1. Giải hệ siêu tĩnh này ta được: 
CAX M
ll
l
M
21
2
 ; CBX M
ll
l
M
21
1
 Biểu đồ phân bố mô men xoắn theo chiều dài (hình 2.5b). 
 Góc xoắn tương đối giữa hai mặt cắt A và C sẽ là: 
11
1
1 0, lx
Gj
xM
p
AX
K   
p
C
p
AX
K
GJ
hP
ll
ll
GJ
lM 00
21
211max
1 .


 (2.3) 
 Góc xoắn tương đối giữa hai mặt cắt C và B sẽ là: 
 43 
22
2
2 0, lx
Gj
xM
p
BX
K   
p
C
p
BX
K
GJ
hP
ll
ll
GJ
lM 00
21
212max
2 .


 (2.4) 
 Góc xoắn tương đối giữa A và B là: 
p
C
KK
GJ
Ph
ll
ll 0
21
21
21
2 

 (2.5) 
 Trong đó G là mô dun đàn hồi trượt của vật liệu khung xe (với thép 
G=8.10
4
 MN/m
2
), Jρ là mô men quán tính tiết diện ngang của khung xe (bằng 
phương pháp vẽ tìm được Jρ=6,62.10
-8
m
4
). Thay các giá trị vào (2.5), đối với ô 
tô Thaco K165 chở đầy gỗ tìm được góc 05267,0  . 
 Từ biểu thức (2.5) ta thấy góc xoắn θ = 0 chỉ khi hC= 0, khi trọng tâm 
khối gỗ và thân xe nằm ngay trên mặt khung. Điều đó thực tế không thể xẩy ra, 
nghĩa là khung xe thường bị xoắn. 
 Từ công thức (2.3) và (2.4) ta thấy các góc βk1 và βk2 có thể xác định theo 
β0 khi biết các thông số kết cấu của khung xe (vật liệu và kích thước hình học). 
Ta có các biến dạng đàn hồi: 
δ1p= z1p - h1p= (z1 +
2
b
 β1)- h1 ; 
δ1t= z1t - h1t = (z1 -
2
b
 β1)- (h1+ Δ1) ; 
δ2p= z2p - h2p= (z2 +
2
b
 β2) – h2 ; 
δ2t= z2t- h2t = (z2 -
2
b
 β2)- (h2+ Δ2) ; (2.6) 
δn1t=zAt - z1t = (z0 - l1.α0-
2
b
 βk1 ) - ( z1 -
2
b
 β1); 
 δn1p=zAp - z1p = (z0 - l1.α0 + 
2
b
 βk1) - (z1 +
2
b
 β1) 
 δn2t=zBt - z2t = (z0 +l2.α0-
2
b
 βk2 ) - ( z2 -
2
b
 β2); 
 δn2p=zBp - z2p = (z0 + l2.α0 + 
2
b
 βk2) - (z2 +
2
b
 β2); 
 44 
Biểu thức động năng của hệ: 
Động năng của hệ là tổng động năng chuyển động tịnh tiến và chuyển 
động quay của các khối lượng: 
 T = T0+ T1+ T2 (2.7) 
Trong đó: T0: Động năng của phần được treo 
 .
2
1
2
1
)(
2
1 2
00
2
00
2
0
2
000   yx JJxzmT 
 T1: Động năng của trục cặp bánh cầu trước 
 .
2
1
)(
2
1 2
11
2
1
2
111 

xJxzmT 
 T2: Động năng của trục cặp bánh cầu sau 
 .
2
1
)(
2
1 2
22
2
2
2
222 

xJxzmT 
 Từ các biểu thức trên ta có biểu thức động năng theo các tọa độ suy rộng là: 
.
2
1
2
1
2
1
.
2
1
2
1
2
1
2
1
))(
2
1
2
22
2
11
2
00
2
00
2
22
2
11
2
00
2
0210



xxx
y
JJJ
JzmzmzmxmmmT
 (2.8) 
 Vì coi khung không biến dạng dọc, nên x1=x2=x0. 
Biểu thức thế năng của hệ: 
Dao động được xét quanh vị trí cân bằng tĩnh nên không kể đến thế năng 
của trọng lực, hệ chỉ có thế năng của lực đàn hồi. Do các cơ cấu đàn hồi là các 
bánh lốp và nhíp có cấu tạo bên phải và trái đối xứng, nên: 
 ci t = ci p = ci , cni t = cni p= cni , (i =1, 2) 
Trong tính toán kỹ thuật, khi có kể đến đặc tính phi tuyến của các cơ cấu 
đàn hồi thì quan hệ giữa lực đàn hồi và lực cản dao động với biến dạng có thể 
lấy gần đúng là : Pđh=ci1δi + ci2δ
2
i và Ri=ki
i
 . 
Trong đó ci1 là độ cứng bộ phận đàn hồi tuyến tính có thứ nguyên N/m; ci2 
là độ cứng bộ phận đàn hồi phi tuyến có thứ nguyên N/m2. 
Do đó thế năng của hệ được xác định từ vị trí cân bằng tĩnh bằng số gia 
thế năng của tất cả các phần tử đàn hồi: 
 45 
 32
2
1 .
3
1
.
2
1
iiiii cc   
và hàm hao tán sẽ có dạng : 
2.
2
1
iii k 
  
Trong đó ci1, ci2 và ki là các hệ số độ cứng và hệ số cản giảm chấn của 
phần tử đàn hồi thứ i, chúng có độ lớn được xác định bằng thực nghiệm. 
Áp dụng với xe tải chở gỗ ta có biểu thức thế năng của hệ trong trạng thái 
này sẽ là: 
 3232223232222222222222
3
1
3
112
3
1
3
112
2
1
2
11
2
1
2
11
3
1
3
1
)(
2
1
)(
2
1
3
1
3
1
)(
2
1
)(
2
1
pntnnptpntnnpt
ptnptpntnnpt
cccc
cccc


 
 Từ các biểu thức (2.6) ta có biểu thức thế năng theo các tọa độ suy rộng là: 
.)
22
()
22
(
2
)
2
()
2
(
3
)
22
()
22
(
3
)
2
()
2
(
3
)
22
()
22
(
2
)
2
()
2
(
2
)
22
()
22
(2
2
)
2
()
2
(
2
3
222020
3
222020
223
222
3
222
22
3
111010
3
111010
123
111
3
111
12
2
222020
2
222020
212
222
2
222
21
2
111010
2
111010
112
111
2
111
11
 
  
  
  
  
b
z
b
lz
b
z
b
lz
c
h
b
zh
b
z
c
b
z
b
lz
b
z
b
lz
c
h
b
zh
b
z
c
b
z
b
lz
b
z
b
lz
c
h
b
zh
b
z
c
b
z
b
lz
b
z
b
lz
c
h
b
zh
b
z
c
kk
n
tp
kk
n
tp
kk
n
tp
kk
n
tp
 (2.9) 
Biểu thức hàm hao tán của hệ: 
Tương tự như thế năng, hàm hao tán của hệ được tính theo biểu thức: 
).(
2
1
)(
2
1
)(
2
1
)(
2
1
2
2
2
22
2
2
2
22
2
1
2
11
2
1
2
11
pntnnpt
pntnnpt
kk
kk




 
Hay: 
 46 
.)
22
()
22
(
2
)
2
()
2
(
2
)
22
()
22
(
2
)
2
()
2
(
2
2
222020
2
222020
22
222
2
222
2
2
111010
2
111010
12
111
2
111
1
 
  
  


b
z
b
lz
b
z
b
lz
k
h
b
zh
b
z
k
b
z
b
lz
b
z
b
lz
k
h
b
Zh
b
z
k
kk
n
tP
kk
n
tP
(2.10) 
Trong đó 1k và 2k tính theo (2.4) và (2.5). 
Biểu thức lực suy rộng : 
 Dao động sinh ra chỉ do kích động động học từ sự mấp mô mặt đường, 
nên các lực suy rộng không thế là các thành phần phản lực tại điểm tiếp xúc giữa 
bánh xe với mặt đất. 
 Khi bánh xe lăn không trượt trên bề mặt mấp mô của đường thì phản lực 
N của đất lên bánh xe sẽ có 2 thành phần theo các phương thẳng đứng và nằm ngang : 
XZ NNN 
 Gọi tải trọng phân bố lên cặp bánh xe thứ i là Pi thì các thành phần phản 
lực này sẽ là : NZi = Pi; 
 NXi = Pi.tgθi= Pi.h
’
i (i=1, 2). (2.12) 
Trong đó: θi – góc giữa tiếp tuyến của đường cong mặt đường với trục OX. 
 tgθi = dhi/ dx = h
’
i . 
Theo giả thiết đã nêu, đề tài chỉ xét dao động quanh vị trí cân bằng tĩnh 
nên: NZ1+NZ2=P1+P2=P, luôn cân bằng với tải trọng, không là lực suy rộng; 
 Thành phần lực NXi thu về tâm bánh xe gây ra mô men quay thân xe 
quanh trục OY: 
 MYi = NXi.Hi = Pi.h
’
i.Hi ,(i=1, 2). (2.13) 
 Với Hi là khoảng cách theo phương thẳng đứng từ trọng tâm xe đến trục 
các bánh xe. 
 Công nguyên tố trong di chuyển khả dĩ của xe là: 
 02121 )()(   YYXX MMxNNA 
 Từ (2.12), (2.13) suy ra: 
 47 
;)(
2
)(
2
)(
;)(
2
)(
2
)(
222
2
111
1
21
*
22
2
11
1
21
*
ptrptrYYo
ptrptrXXX
hhH
P
hhH
P
MMQ
hh
P
hh
P
NNQ
 (2.14) 
Trong đó h/itr và h
/
ip tính theo dạng bề mặt mấp mô tại điểm tiếp xúc của 
bánh xe trái và phải trong cặp thứ i. 
 Dạng mấp mô mặt đường được biểu diễn qua hàm độ cao mấp mô tại vị 
trí tiếp xúc của các bánh xe hi (t), i = 1, 2. Chúng được xác định từ các kết quả 
thực nghiệm. 
Phương trình vi phân dao động của hệ: 
 Phương trình vi phân (PTVP) dao động của hệ viết theo các tọa độ suy 
rộng được lập từ phương trình Lagranger loại 2: 
*
i
iiii
Q
qqq
T
q
T
dt
d









 (2.15) 
Trong đó: T, Π và Φ là động năng, thế năng và hàm hao tán của hệ; Q*i là 
lực suy rộng không thế tương ứng với tọa độ suy rộng qi (i = 1, 2, 7). 
 Sau khi tính đạo hàm các biểu thức động năng, thế năng và hàm hao tán 
theo các biến tương ứng rồi thay vào phương trình (2.15) ta nhận được hệ PTVP: 
 abzlzzzlbzblzc
b
zlzzzl
b
z
b
lzc
zczclclczcc
zkzklklkzkkzm
kkn
kkn
nnnnnn
nnnnnn
;0
4
)
44
(2
4
)
44
(2
22)(2)(2
22)(2)(2
22
2
20220002
2
2
2
2
2
2
2
2
2
0
2
2
2
022
11
2
10110001
2
1
2
2
1
2
1
2
2
0
2
1
2
012
221111022111102111
22110221102100
  
  
 
  bhhHPQ
b
zlzzzl
b
z
b
lzcl
b
zlzzzl
b
z
b
lzcl
zlczlclclczlclc
zlkzlklklkzlklkJ
ipiti
i
i
n
n
nnnnnn
nnnnnny
;
444
2
444
2
22)(2)(2
22)(2)(2
2
1
0
20
2
02202002
2
2
2
2
2
2
0
2
2
0
2
2
2
0222
10
2
01101001
2
1
2
2
1
2
0
2
2
0
2
1
2
0121
222111110
2
221
2
1110221111
2221110
2
22
2
110221100

  
  
 
 48 
 )(;2)()(
444
2
)(
2
)(
4
2
)(222)(222
2
1
2
1121111111
11
2
01110001
2
1
2
2
1
2
1
2
2
0
2
1
2
012
111111
2
1
2
2
112
111110111011`1110110111
chhchhchhk
b
zlzzzl
b
z
b
lzc
hh
b
hhz
b
zc
zcclczczkklkzkzm
ptptpt
kkn
ptpt
nnnnnn


  

)(;)(2)()(
444
2
)(
2
)(
4
2
)(222)(222
2
2
2
2222221222
22
2
02220002
2
2
2
2
2
2
2
2
2
0
2
2
2
022
222222
2
2
2
2
222
221210221021`2220220222
dhhchhchhk
b
Zlzzzl
b
z
b
lzc
hh
b
hhz
b
zc
zcclczczkklkzkzm
ptptpt
kkn
ptpt
nnnnnn


  

 
  )(;0)()()(
)()()(
22
)(
2
22
)(
2
222
2
0222022
2
22
111
2
0111011
2
12
221
2
111
2
221111
2
22
2
11
2
121
2
00
ezbblzbc
zbblzbc
c
b
c
b
cc
b
k
b
k
b
kk
b
J
kkkn
kkkn
nnknkn
nnknnx
 
 

 
)()];()()([
2
2
)()(
2
)(
2
)(
2
)(
22
)(
22
2
1
2
1121111111
10
2
10100110012
111
2
11111
2
12
11111
2
011
2
111
2
01
2
11
ghhchhkhhc
b
b
zbblbz
b
c
hh
b
hhbzz
b
c
cc
b
c
b
kk
b
k
b
J
tptptp
n
pttp
nnnnx


 


)()];(()([
2
2
)()(
2
)(
2
)(
2
)(
22
)(
22
2
2
2
2222222221
20
2
20200220022
222
2
11222
2
22
22121
2
021
2
222
2
02
2
22
hhhchhkhhc
b
b
zbblbz
b
c
hh
b
hhbzz
b
c
cc
b
c
b
kk
b
k
b
J
ptntptp
n
tppt
nnnnx


 


 (2.16) 
 49 
 Giải hệ phương trình vi phân (2.16) sẽ cho ta góc lắc β0, từ đó xác định 
được các góc xoắn θ theo biểu thức (2.5). 
 Khảo sát góc xoắn θ từ (2.5) sẽ xác định được một số thông số kết cấu 
hoặc chế độ làm việc hợp lý theo các điều kiện bền và điều kiện cứng khung xe. 
Các phương trình trong hệ (2.16) có thể viết dưới dạng ma trận như sau: 
 ,2SGqDqqCqBqM  (2.18) 
Trong đó: M, B, C, và G, S2 – là các ma trận hệ số, chúng được xác định 
từ hệ số của từng số hạng trong các phương trình của hệ (2.16). 
q = 
2
1
0
2
1
0
0



z
z
z
; M = 
x
x
x
Y
J
J
J
m
m
J
m
2
1
0
2
1
0
0
000000
000000
000000
000000
000000
000000
000000
; 
B= 
)(
2
0
2
0000
0)(
22
0000
22
)(
2
0000
000)(2022
0000)(222
00022)(2)(2
00022)(2)(2
22
2
2
2
11
2
1
2
2
2
1
2
21
2
22222
11111
2211
2
22
2
112211
21221121
nn
nn
nnnn
nnn
nnn
nnnnnn
nnnnnn
kk
b
k
b
kk
b
k
b
k
b
k
b
kk
b
kklkk
kklkk
lklklklklklk
kklklkkk
 50 
C=
 2121
2
21
2
1111
2
11
2
21
2
11
2
2111
2
212122121
111111111
221111
2
221
2
111221111
21112211112111
2
0
2
0000
0
22
0000
22
)(
2
0000
000)(2022
0000)(222
00022)(2)(2
00022)(2)(2
nn
nn
nnnn
nnn
nnn
nnnnnn
nnnnnn
cc
b
c
b
cc
b
c
b
c
b
c
b
cc
b
cclcc
cclcc
lclclclclclc
cclclccc
D=
0000000
0000000
0000000
)(
2
0
2
)(2022
0)(
22
0)(222
22
)(
2
22)(2)(2
22
)(
2
22)(2)(2
22222
2
022
2
222220
2
222022
11212
2
012
2
112120
2
12012
2222
2
1112
2
0222112
2
222211120
3
222
3
1120222112
222
2
112
2
02212
2
2221120
2
222
2
11202212
1
 
 
 
 
nnnnn
nnnnn
nnnnnnnnnn
nnnnnnnnnn
cc
b
c
b
zcclczc
cc
b
c
b
zcclczc
lc
b
lc
b
lclc
b
zlczlclclczlclc
c
b
c
b
cc
b
zczclclczcc
G = 
   )(
2
0
4
0)(
2
)(
2
0)(
24
0)(
2
)(
2
)(
2
000
]
)(0
2
)([2022
]
0)(
2
0)(222
424
)(2)(222
444
)(2)(222
22
2
222
3
222222202
2
2220
2
22
11
2
121
3
1211120
2
12101
2
1210
2
12
20
2
2210
2
12
20222
10112
2022
10122
022
2222222
2
222222220222
0112
12112
2
111211120112
0222
2
0112
2
2222
2
0202220101120
2
2220
2
112
022
2
012
2
222112
2
020220101202220112
tpnptnn
ptnptnnn
nn
n
n
n
n
n
ptntpnn
n
pttpnnn
nnnnnnn
nnnnnnnn
hh
b
c
b
chhbcl
b
c
b
c
hh
b
c
b
chhbc
b
cl
b
c
b
c
bcbc
lc
lc
b
c
c
b
c
hhbcc
b
hhczlclc
Zlc
hhbcc
b
hhczlclc
lc
b
lc
b
lc
b
lzlclzlczlclc
c
b
c
b
cc
b
lzclzczlclc








 
 
 
 
 51 
S2=
 
 
 
 )()()(
2
)()()(
2
0
)(2)()(
)(2)()(
0
2
2
2
2222221222
2
1
2
1121111111
2
2
2
2222221222
2
1
2
1121111111
2
1
11
pttptp
tptptp
pttptp
pttptp
i
ptii
hhchhchhk
b
hhchhchhk
b
hhchhchhk
hhchhchhk
hhHP
 




Nếu không kể đến đặc trưng phi tuyến của các phần tử đàn hồi thì ta sẽ có 
hệ PTVP dao động như sau: 
 azczclclczcc
zkzklklkzkkzm
nnnnnn
nnnnnn
;022)(2)(2
22)(2)(2
221111022111102111
22110221102100
 
 bQzlczlclclczlclc
zlkzlklklkzlklkJ
nnnnnn
nnnnnny
;22)(2)(2
22)(2)(2
222111110
2
221
2
1110221111
2221110
2
22
2
110221100
 
)(;)()(
)(222)(222
1111111
111110111011`1110110111
chhchhk
zcclczczkklkzkzm
ptrptr
nnnnnn

 
)();()(
)(222)(222
2221222
221210221021`2220220222
dhhchhk
zcclczczkklkzkzm
ptrpt
nnnnnn

 
)(;0
22
)(
2
22
)(
2
221
2
111
2
02111
2
22
2
11
2
021
2
00
ec
b
c
b
cc
b
k
b
k
b
kk
b
J
nnnn
nnnnx

 
)()];()([
2
)(
22
)(
22
1111111
11211
2
011
2
111
2
01
2
11
ghhkhhc
b
cc
b
c
b
kk
b
k
b
J
tptp
nnnnx


 
)()];()([
2
)(
22
)(
22
2222221
22121
2
021
2
222
2
02
2
22
hhhkhhc
b
cc
b
c
b
kk
b
k
b
J
tptp
nnnnx


 
 (2.19) 
Đặc biệt khi xe di chuyển trên đoạn đường không có độ chênh mấp mô 
giữa các bánh xe bên trái và bên phải (hit= hip) thì vế phải của các phương trình 
 52 
(5), (6), (7) đều bằng không, nên các góc lắc β1= β2 = β0= 0 . Khi đó θ = 0, khi 
đó khung xe không bị xoắn. 
 Hệ phương trình (2.16) có thể tách thành 2 hệ riêng và khảo sát chúng 
một cách độc lập nhau: 
- Các phương trình (a, b, c, d): PTVP dao động thẳng đứng phần được 
treo, và không được treo không phụ thuộc vào các dao động lắc ngang βi 
(i=0,1.2). 
- Các phương trình (e, g, h): PTVP dao động lắc ngang của phần được 
treo và các trục bánh xe, không phụ thuộc vào các dao động thẳng đứng Zi 
(i=0,1.2). 
Các phương trình trong các hệ trên có thể viết dưới dạng ma trận như sau: 
 ,SqCqBqM  (2.20) 
Trong đó: M, B, C, và S: Các ma trận hệ số, chúng được xác định từ hệ số 
của từng số hạng trong các phương trình của hệ (2.19). 
Với hệ 1, ma trận hệ số được xác định từ 4 phương trình (a, b, c, d) trong 
(2.19) như sau: 
M = 
2
1
0
0
000
000
000
000
m
m
J
m
y ; 
B = 
)(2022
0)(222
22)(2)(2
22)(2)(2
22222
11111
2211
2
22
2
112211
21221121
nnn
nnn
nnnnnn
nnnnnn
kklkk
kklkk
lklklklklklk
kklklkkk
C = 
)(2022
0)(222
22)(2)(2
22)(2)(2
212122121
111111111
221111
2
221
2
111221111
21112211112111
nnn
nnn
nnnnnn
nnnnnn
cclcc
cclcc
lclclclclclc
cclclccc
 53 
S = 
 
 )()(
)()(
2
1
0
2221222
1111111
2
1
tptp
tptp
ipitii
i
hhchhk
hhchhk
hhHP
 


; q = 
2
1
0
0
Z
Z
Z
 . 
(2.21) 
Với hệ 2 (PTVP dao động lắc ngang βi), các ma trận hệ số được xác định 
từ 3 phương trình sau của (2.19) như sau: 
 M = 
x
x
x
J
J
J
2
1
0
00
00
00
 ; 
 B = 
)(
2
0
2
0)(
22
22
)(
2
22
2
2
2
11
2
1
2
2
2
1
2
21
2
nn
nn
nnnn
kk
b
k
b
kk
b
k
b
k
b
k
b
kk
b
 ; 
 C = 
 2121
2
21
2
1111
2
11
2
21
2
11
2
2111
2
2
0
2
0
22
22
)(
2
nn
nn
nnnn
cc
b
c
b
cc
b
c
b
c
b
c
b
cc
b
 ; 
S =  
 )()(
2
)()(
2
0
2221222
1111111
tptp
tptp
hhchhk
b
hhchhk
b

 ; q = 
2
1
0



 ; 
(2.22) 
2.4. Mô hình dao động khi kể đến xoắn khung, dao động ở hai cầu 
độc lập nhau 
 Mô hình dao động toàn xe tổng quát có kể đến xoắn khung, dao động ở 
hai cầu độc lập nhau giới thiệu ở hình 2.6. 
 54 
Hình 2.6. Mô hình dao động ô tô có kể đến xoắn khung, dao động hai cầu độc lập nhau
 55 
 Trong trường hợp này có thêm 2 giả thiết: Xoắn khung xe là xoắn phẳng 
và 21
2 ll , trong đó là bán kính quán tính của phần được treo, 21, ll là khoảng 
cách theo phương nằm ngang từ trọng tâm ô tô đến cầu trước và cầu sau; 
 độ cứng chống xoắn của khung xe trong trường hợp này là xC . 
 Khối lượng phần được treo được phân ra hai khối lượng: Khối lượng 
được treo phân bố lên cầu trước 1km và khối lượng được treo phân bố lên cầu sau 
2km . Trên sơ đồ hình 2.6: 
 zk1, βk1: Dịch chuyển thẳng đứng và góc lắc ngang của khối lượng được 
treo phân bố lên cầu trước; 
 zk2, βk2: Dịch chuyển thẳng đứng và góc lắc ngang của khối lượng được 
treo phân bố lên cầu sau; 
 z1, β1: Dịch chuyển thẳng đứng và góc lắc ngang của khối lượng không 
được treo cầu trước; 
 z2, β2: Dịch chuyển thẳng đứng và góc lắc ngang của khối lượng không 
được treo cầu sau; 
 mk1, jk1: Khối lượng được treo phân bố lên cầu trước, mô men quán tính của 
khối lượng được treo phân bố lên cầu trước đối với trục đối xứng dọc của ô tô; 
 mk2, jk2: Khối lượng được treo phân bố lên cầu sau, mô men quán tính của 
khối lượng được treo phân bố lên cầu sau đối với trục đối xứng dọc của ô tô; 
 m1, j1: Khối lượng không được treo cầu trước, mô men quán tính của khối 
lượng không được treo cầu trước đối với trục đối xứng dọc; 
 m2, j2: Khối lượng không được treo cầu sau, mô men quán tính của khối 
lượng không được treo cầu sau đối với trục đối xứng dọc; 
 Ct: Độ cứng chống lắc ngang của hệ thống treo cầu trước; 
 Cs: Độ cứng chống lắc ngang của hệ thống treo cầu sau; 
 Cx: Độ cứng xoắn của khung xe theo phương dọc xe; 
 q1t, q1p: Chiều cao mấp mô mặt đường tại vị trí bánh xe trước trái và trước phải; 
 q2t, q2p: Chiều cao mấp mô mặt đường tại vị trí bánh xe sau trái và sau phải; 
 e1 , e2: Khoảng cách giữa hai nhíp của hệ thống treo cầu trước và sau; 
 56 
 Hạn chế của việc khảo sát mô hình dao động ở hai cầu độc lập nhau này là 
không thể xác định được đặc tính dao động của những điểm nằm ngoài các điểm 
tương ứng ở các cầu trước và sau, cũng như không khảo sát được dao động góc 
dọc của ô tô. 
 2.4.1. Thiết lập phương trình vi phân dao động của khối lượng được treo 
phân bố lên cầu trước và khối lượng không được treo cầu trước 
 Mô hình dao động của các khối lượng được treo phân bố lên cầu trước và 
khối lượng không được treo cầu trước giới thiệu ở hình 2.7. 
Hình 2.7. Mô hình dao động của khối lượng được treo phân bố lên cầu trước và 
khối lượng không được treo cầu trước 
 Sử dụng nguyên lý D’Alambert để thiết l