Tóm tắt Luận án Nghiên cứu biện pháp nâng cao các đặc tính khí động cánh máy bay không người lái

 dây cung và phương sải cánh); Gốc tọa độ thuộc mặt 
phẳng đối xứng và nằm tại mép trước cánh; 
2.2.2. Đề xuất phương pháp xác định mặt cong trung bình đáp ứng phân 
bố tải khí động cho trước trên cánh 
 Luận án xây dựng được hệ phương trình đại số tuyến tính (2.16) xác định 
các góc tấn cục bộ (độ dốc cục bộ đường trung bình tại các mặt cắt khác 
nhau): 
 ̅
 ∑ ∑ ̅ ̅ (2.16) 
trong đó: n, N là số dải chia theo phương sải cánh và dây cung cánh; i, j là chỉ 
 ̅ 
số đặc trưng cho vị trí của xoáy theo hàng dọc, hàng ngang; là đạo hàm 
cường độ xoáy trên ô thứ ij theo góc ; ̅ là tải khí động tại ô thứ ij của 
mặt cong dưới góc tấn α; ̅ là tải khí động tại ô thứ ij của tấm phẳng dưới 
góc tấn α; 
 Tích phân các góc tấn cục bộ , khi đó xây dựng được công thức xác 
định tọa độ yij tương ứng với tọa độ xij của mặt cong: 
 ̅̅ ̅̅ ̅
{ (2.17) 
 ̅̅̅̅̅ ̅̅̅̅̅
 ∑ ( ) 
 Tập hợp các điểm (xij, yij) xác định mặt cong trung bình cánh thỏa mãn 
phân bố tải khí động cho trước. 
2.2.3. Xác định hình dạng cánh theo mặt cong trung bình 
 Bản chất là bồi thêm bề dày cho mặt cong trung bình, ví dụ theo dạng 
profile NACA [37]. 
2.2.4. Kết quả tính toán hình dạng cánh một lớp cận tối ưu 
 Trên cơ sở các mục từ 2.2.1-2.2.3 thiết lập được chương trình phần mềm 
tính toán xác định hình dạng cánh một lớp cận tối ưu. 
 Tính toán cánh một lớp cận tối ưu với các số liệu đầu vào: 
 0
+ Hệ số lực nâng của cánh =0.8; góc tấn tính toán =8 ; 
+ Dây cung b=0.337[m]; sải cánh L=1[m]; 
+ Độ dày tương đối lớn nhất ̅ =12%; n=N=41; 
 6 
 Hình 2.9. Hình dạng một nửa cánh một lớp cận tối ưu tương ứng hệ số lực 
 nâng của cánh =0.8 
 Với hình dạng cánh này, kết quả mô phỏng bằng phần mềm Ansys: 
Cy=0.85, sai khác so với PPXRR (Cy=0.8) là 7%. Sai số nhỏ có thể chấp nhận 
được và khẳng định độ tin cậy chương trình tính toán. 
2.3. Tối ưu hóa hình dạng cánh một lớp 
2.3.1. Xây dựng bài toán tối ưu hóa hệ số lực cản Cx 
 Luận án lựa chọn bộ tham số ( ) để tối ưu hóa hình dạng cánh, 
trong đó α là góc tấn, là góc xoắn hình học bổ sung thêm góc xoắn hình học 
giữa dây cung profile mút cánh và dây cung profile gốc cánh của cánh cận tối 
ưu và hệ số đại diện cho hình dạng mặt cong trung bình của cánh cận tối 
ưu (vừa có xoắn khí động, vừa có xoắn hình học). Bài toán được đặt ra như 
sau: cho trước Cy=const, tìm bộ 3 tham số ( ) sao cho: 
 ( ) với ( ) (2.22) 
 ( ) 
hay ( ) với ( ) (2.23) 
 ( )
điều kiện ràng buộc được thực hiện ở một chế độ bay hành trình với hệ số lực 
nâng . 
2.3.2. Thuật toán tối ưu hóa hệ số lực cản Cx có ràng buộc hệ số lực nâng 
Cy=const bằng phương pháp số theo gradient 
 Hình (2.19) trình bày cách xác định “hướng giảm nhanh nhất” hệ số Cx 
và đảm bảo hệ số Cy “tiệm cận” đến mặt cong ràng buộc 
gần nhất với cùng một bước đi xác định. , là véc tơ gradient hệ số 
Cx, Cy tại điểm tính toán thứ k nằm trên mặt cong ràng buộc Cy=const; là 
hình chiếu của véc tơ trên mặt phẳng vuông góc với véc tơ tại 
điểm tính toán thứ k; Cxmin là hệ số Cx đạt giá trị nhỏ nhất tương ứng với 
nghiệm của bài toán tối ưu hóa. Theo tài liệu [2], [46]: để đi đến điểm tối ưu 
 7 
Cxmin nhanh nhất phải đi theo hướng véc tơ chiếu tại điểm tính toán thứ 
k. Công thức xác định véc tơ chiếu : 
 (2.34) 
 | |
I, P lần lượt là ma trận đơn vị và ma trận chiếu cỡ 3x3. là ma trận 
chuyển vị của ma trận và | | là bình phương mô đun véc tơ . 
Thuật toán số tối ưu hóa được thể hiện trên hình (2.20): 
 Hình 2.19. Cách xác định hướng giảm hệ số Cx nhanh nhất đảm bảo hệ số Cy 
 tiệm cận gần nhất đến mặt cong ràng buộc trong không gian 3 chiều bằng 
 phương pháp số theo gradient 
 Hình 2.20. Thuật toán số tối ưu hóa hệ số Cx có ràng buộc Cy=const 
+ Điểm xuất phát là điểm 1: , tính các véc tơ gradient và , 
tính véc tơ chiếu theo công thức (2.34). Chọn bước đi xác định được 
 8 
điểm . Điểm không nằm trên mặt cong ràng buộc, tại điểm này phải 
điều chỉnh các biến phụ thuộc để xác định được điểm 2: nằm trên mặt 
cong ràng buộc Cy=const. 
+ Điều kiện hội tụ: hệ số Cx bắt đầu tăng hoặc hệ số K bắt đầu giảm, đồng 
thời mô đun véc tơ chiếu | | | |. 
+ Nếu số bước lặp là n thì . 
2.3.3. Kết quả tối ưu hóa và nhận xét 
 Minh họa kết quả tối ưu hóa cánh 1 lớp: 
Dây cung: b=0.337[m]; Sải cánh: L=1[m]; Độ dày tương đối: ̅ =12%; 
Điều kiện ràng buộc: =0.3; Điều kiện tính toán: vận tốc V=30[m/s], 
độ cao H=0[m]; n=41, N=21; Kết quả tối ưu hóa: 
 =11.3 tại điểm ( ) =(2.80, 0.40, 0.3) 
+ Gọi hình dạng cánh tìm được khi tối ưu hóa với điều kiện ràng buộc 
 = 0.3 là cánh tối ưu Cyopt =0.3; 
 0
+ Góc xoắn hình học bổ sung =0.4 không đáng kể. Mặt cong trung bình 
cánh cận tối ưu có góc xoắn hình học về cơ bản là tối ưu; 
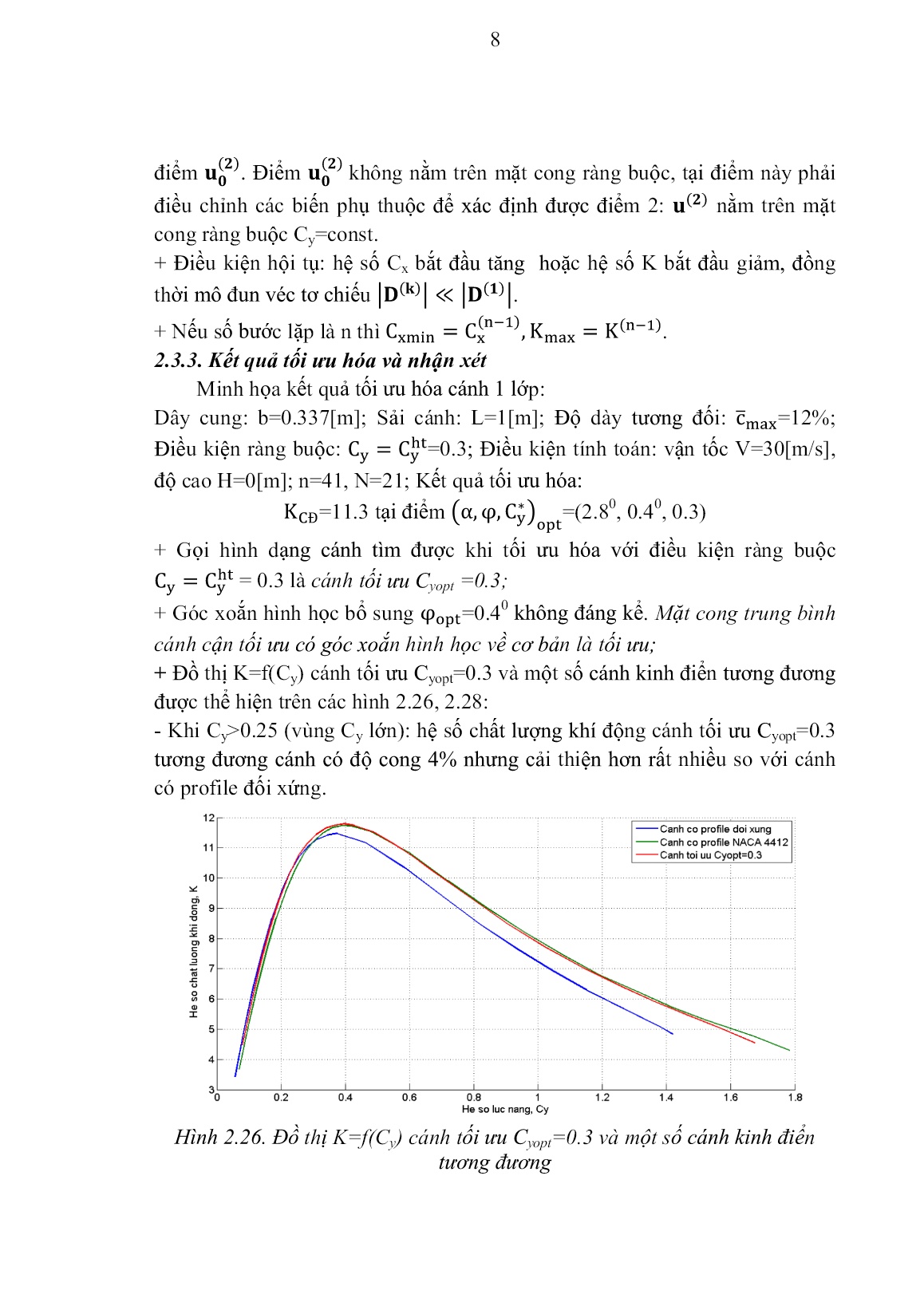
+ Đồ thị K=f(Cy) cánh tối ưu Cyopt=0.3 và một số cánh kinh điển tương đương 
được thể hiện trên các hình 2.26, 2.28: 
- Khi Cy>0.25 (vùng Cy lớn): hệ số chất lượng khí động cánh tối ưu Cyopt=0.3 
tương đương cánh có độ cong 4% nhưng cải thiện hơn rất nhiều so với cánh 
có profile đối xứng. 
 Hình 2.26. Đồ thị K=f(Cy) cánh tối ưu Cyopt=0.3 và một số cánh kinh điển 
 tương đương 
 9 
 Cụ thể khi Cy=1.2: K(cánh tối ưu Cyopt=0.3)=K(cánh có độ cong 
4%)=6.7; K(cánh có profile đối xứng)=6, khi đó hệ số K cánh tối ưu Cyopt=0.3 
và cánh có độ cong 4% cải thiện 12% so với cánh có profile đối xứng. 
- Khi Cy<0.25 (vùng Cy nhỏ): hệ số K cánh tối ưu Cyopt=0.3 cải thiện so với 
cánh có độ cong 4% và giảm so với cánh có profile đối xứng. 
 Hình 2.28. Đồ thị K=f(Cy) cánh tối ưu Cyopt=0.3 và một số cánh kinh điển 
 tương đương vùng hệ số lực nâng Cy nhỏ 
 Cụ thể khi Cy=0.1: K(cánh tối ưu Cyopt=0.3)=5.48; K(cánh có độ cong 
4%)=5.18; K(cánh có profile đối xứng)=5.71, khi đó hệ số K cánh tối ưu 
Cyopt=0.3 cải thiện 6% so với cánh có độ cong 4% và giảm 4% so với cánh có 
profile đối xứng. 
 Nhận xét chung: 
+ Hình dạng cánh tối ưu là hình dạng cánh cận tối ưu có hệ số lực nâng xác 
định mặt trung bình và bay với góc tấn α=αopt. Trong đó và 
αopt là nghiệm của bài toán tối ưu hóa . 
+ Cánh tối ưu đã “dung hòa” hệ số lực cản Cx các cánh kinh điển có độ cong 
khác nhau (profile không đổi theo sải cánh). 
+ Bằng cách nào đó thay đổi được mặt cong trung bình đến mặt cong trung 
bình các cánh tối ưu (với ràng buộc khác nhau) thì hệ số Cx 
sẽ giảm đáng kể so với tất cả các cánh kinh điển ở mọi chế độ bay hành trình 
với hệ số Cy khác nhau. 
2.3.4. So sánh cánh tối ưu và cánh chim 
 Sự tương đồng giữa cánh tối ưu và cánh chim (hình 2.32): 
 10 
 Hình 2.32. So sánh cánh tối ưu và cánh chim 
+ Đường trung bình profile tại các thiết diện có độ cong giảm dần theo thứ tự 
từ gốc cánh đến mép ngoài của cánh; 
+ Dây cung profile tại các thiết diện “vặn” theo chiều làm giảm góc tấn cục 
bộ cũng theo thứ tự từ gốc cánh đến mép ngoài của cánh. 
+ Cánh tối ưu và cánh chim vừa có xoắn khí động (profile thay đổi tại các mặt 
cắt khác nhau) và xoắn hình học (các profile xoắn tương đối với nhau). 
 Trong quá trình bay ở tốc độ, độ cao khác nhau (Cy khác nhau), cánh 
chim sẽ thay đổi hình dạng (chủ yếu là thay đổi mặt cong trung bình) để thích 
nghi đến các chế độ bay đó. Như vậy, cánh tối ưu một phần nào đó giải thích 
cánh chim - tối ưu hóa của thiên nhiên. 
 Thiết kế Winglets 
 Hình 2.33. Thiết kế Winglets trên cánh máy bay Boeing 737 
 Sự tương đồng giữa mép ngoài phía sau cánh tối ưu và thiết kế Winglets 
(hình 2.33): tại mép ngoài phía sau của cánh “vểnh lên” đột ngột, điều này 
khá tương đồng với thiết kế Winglets. Bản chất vật lý của dạng hình học này 
 11 
chính là làm giảm cường độ xoáy tại mép ngoài của cánh, do đó sẽ giảm được 
đáng kể lực cản cảm ứng trên cánh và tiết kiệm được lượng nhiên liệu vận 
hành. 
2.4. Kết luận chương 2 
 Đề xuất phương pháp, phát triển thuật toán và phần mềm xác định hình 
dạng cánh một lớp tối ưu “dung hòa” được hệ số lực cản các cánh kinh điển 
có độ cong khác nhau và một phần nào đó giải thích cánh chim - tối ưu hóa 
của thiên nhiên. 
 Chương 3. TỐI ƯU HÓA CÁNH NHIỀU LỚP 
3.1. Đặt vấn đề 
 Chương 3 trình bày kết quả tối ưu hóa một số phương án cánh nhiều lớp. 
Cụ thể là tối ưu hóa góc tấn và vị trí tương đối giữa các cánh thành phần ở các 
chế độ bay hành trình với hệ số Cy khác nhau và chế độ cất hạ cánh. 
3.2. Tối ưu hóa cánh nhiều lớp phẳng 
 Cánh nhiều lớp có các cánh thành phần là profile đối xứng và giống nhau 
gọi là cánh nhiều lớp phẳng. 
3.2.1. Xây dựng các bài toán tối ưu hóa 
* Xác định bộ tham số tối ưu hóa (hình 3.1): 
 Có các định nghĩa: α là góc tấn (quy ước là góc tấn cánh 1); δ1, δ2 là góc 
lệch cánh 2, cánh 3 so với cánh 1 (góc giữa dây cung profile cánh 2, cánh 3 so 
với dây cung profile cánh 1 tại một mặt cắt qua cánh; δ1, δ2 >0 khi cánh 2, 
cánh 3 “vểnh xuống” so với cánh 1); b là chiều dài dây cung các cánh thành 
phần; b0 là chiều dài dây cung cánh ba lớp; h1, h2 lần lượt là kích thước khe hở 
giữa cánh 1 và cánh 2, cánh 2 và cánh 3; 
 Hình 3.1. Tham số hình học mặt cắt vuông góc với sải cánh của mô hình 3 
 tấm phẳng 
 Mặc dù các kích thước liên quan đến khe hở (h1, h2) ảnh hưởng khá 
nhiều đến hệ số lực cản Cx (khi Cy lớn) và hệ số Cymax nhưng góc lệch của các 
cánh thành phần (δ1,δ2) được chứng minh ảnh hưởng mạnh hơn rất nhiều và 
để giảm khối lượng tính toán thì luận án lựa chọn bộ tham số (α, δ1, δ2) để tối 
ưu hóa cánh 3 lớp. 
 12 
* Các bài toán tối ưu hóa: 
+ Bài toán 1: Cho trước , tìm bộ tham số thỏa 
mãn các điều kiện: 
 với ràng buộc (3.2) 
hay , (3.3) 
+ Bài toán 2: Tìm bộ tham số sao cho: 
 ( ) (3.4) 
 Thuật toán giải bài toán 1 đã được trình bày trong chương 2. Dưới đây 
trình bày thuật toán số giải bài toán 2 không có ràng buộc. 
3.2.2. Thuật toán số tối ưu hóa hệ số Cymax bằng phương pháp gradient 
 Hình 3.3. Cách xác định hướng tăng hệ số Cy nhanh nhất trong không gian 2 
 chiều bằng phương pháp số theo gradient 
 Hình (3.3) trình bày cách xác định “hướng tăng nhanh nhất” hệ số Cy 
đến điểm tối ưu bằng phương pháp số. 
 Theo tài liệu [2], [46]: để đi đến điểm tối ưu nhanh nhất phải đi theo 
hướng véc tơ gradient hệ số lực nâng với bước đi tại điểm tính 
toán thứ k. 
3.2.3. Kết quả tối ưu hóa và nhận xét 
 Tối ưu hóa cánh 3 lớp phẳng: dây cung b0=0.337[m]; sải cánh L=1[m]; 
h1=h2=2%b0; các cánh thành phần có profile đối xứng (NACA 0012). 
* Kết quả tối ưu hóa hệ số chất lượng khí động (hệ số lực cản Cx): 
 Đồ thị K=f(Cy) và đồ thị cực tuyến Cy=f(Cx) cánh 3 lớp phẳng tại các 
điểm tối ưu và một số cánh một lớp tương đương (hình 3.4). 
 13 
 Hình 3.4. Đồ thị phụ thuộc hệ số chất lượng khí động vào hệ số lực nâng K=f(Cy) 
 cánh 3 lớp phẳng tại các điểm tối ưu và một số cánh một lớp tương đương 
+ Khi Cy=0.2 (đại diện hệ số Cy nhỏ): 
K(cánh 3 lớp phẳng tại điểm tối ưu)=10.7; K(cánh có độ cong 4%)=9.1; 
K(cánh tối ưu Cyopt=0.3)=K(cánh có profile đối xứng)=9.5; 
Khi đó hệ số chất lượng khí động cánh 3 lớp phẳng tại điểm tối ưu: 
- Tăng 12% so với cánh tối ưu Cyopt=0.3 và cánh có profile đối xứng; 
- Tăng 17% so với cánh có độ cong 4%. 
+ Khi Cy=1.4 (đại diện hệ số Cy lớn): 
K(cánh 3 lớp phẳng tại điểm tối ưu)=6.46; K(cánh có profile đối xứng)=4.94; 
K(cánh tối ưu Cyopt=0.3)=K(cánh có độ cong 4%)=5.8; 
Khi đó hệ số chất lượng khí động cánh 3 lớp phẳng tại điểm tối ưu: 
- Tăng 11% so với cánh tối ưu Cyopt=0.3 và cánh có độ cong 4%; 
- Tăng 31% so với cánh có profile đối xứng. 
+ Ở các chế độ bay hành trình với hệ số Cy khác, cánh 3 lớp phẳng tại các 
điểm tối ưu vẫn duy trì cải thiện đáng kể hệ số chất lượng khí động so với 
cánh 1 lớp. 
 Như vậy cánh 3 lớp phẳng có hệ số chất lượng khí động (hay hệ số Cx) 
tại các điểm tối ưu được cải thiện rất nhiều (từ 11%-31%) so với cánh 1 lớp 
tương đương ở tất cả các chế độ bay hành trình với hệ số Cy khác nhau. 
* Kết quả tối ưu hóa hệ số lực nâng lớn nhất Cymax: 
 ( ) =2.45 tại điểm =(80, 29.50, 54.10) 
Mô phỏng bằng phần mềm Ansys, tính được: 
+ Cymax (cánh có profile đối xứng)=1.44; 
+ Cymax (cánh có độ cong 4%)=1.83; 
 14 
 Hệ số Cymax cánh 3 lớp phẳng tại điểm tối ưu tăng 70% so với cánh có 
profile đối xứng và tăng 34% so với cánh có độ cong 4%. 
3.3. Tối ưu hóa cánh nhiều lớp có mặt cong trung bình đáp ứng phân bố 
tải khí động cho trước 
 Phần này trình bày kết quả mặt cong trung bình cánh nhiều lớp (minh 
họa cánh 3 lớp có dây cung các cánh thành phần bằng nhau) đáp ứng phân bố 
tải khí động cho trước trên cánh gồm phân bố tải khí động trên từng cánh 
thành phần đảm bảo dòng chảy tiến nhập êm và tối ưu theo lý thuyết mặt nâng 
tuyến tính đối với cánh mỏng như đã đề cập trong chương 2. Với mặt cong 
trung bình tìm được, bồi đắp thêm độ dày cho từng cánh thành phần theo 
dạng profile NACA đối xứng để được hình dạng cánh nhiều lớp cận tối ưu. 
Sau đó sử dụng bộ tham số (α, δ1, δ2) để tối ưu hóa hệ số Cx, Cymax cánh 3 lớp 
cận tối ưu ở các chế độ bay khác nhau. Các tham số này được định nghĩa lại: 
+ α: góc tấn (quy ước là góc tấn tiết diện giữa của cánh 1); 
+ δ1, δ2: lần lượt là góc lệch của cánh 2, cánh 3 so với cánh 1 (là góc giữa dây 
cung profile giữa cánh của cánh 2, cánh 3 so với dây cung profile giữa cánh 
của cánh 1). δ1, δ2 >0 khi cánh 2, cánh 3 “vểnh xuống” so với cánh 1. 
 Kết quả tối ưu hóa và nhận xét: 
* Kết quả xác định hình dạng cánh 3 lớp cận tối ưu (hình 3.8, 3.9). 
 Hình 3.8. Mặt cong trung bình cánh 3 lớp cận tối ưu =0.8 
 Hình 3.9. Hình dạng cánh 3 lớp cận tối ưu =0.8 
 15 
 Kết quả tính bằng phần mềm Ansys: Cy=0.87, sai số so với PPXRR là 
11% có thể chấp nhận được và khẳng định độ tin cậy chương trình tính toán. 
* Kết quả tối ưu hóa hệ số chất lượng khí động: tối ưu hóa cánh 3 lớp cận tối 
ưu =0.8 với ràng buộc =1.5: 
 0 0 0
 =6.15 tại điểm =(3.8 , 6.3 , 22.6 ) 
Tương ứng với hệ số Cy=1.5: K (cánh có profile đối xứng)=4.8; K (cánh có 
độ cong 4%)=5.2; 
 Vậy hệ số chất lượng khí động cánh 3 lớp cận tối ưu =0.8 tại điểm tối 
ưu tăng 28% so với cánh có profile đối xứng, tăng 18% so với cánh có độ 
cong 4%. 
* Kết quả tối ưu hóa hệ số lực nâng lớn nhất Cymax: 
 Kết quả tối ưu hóa hệ số Cymax cánh 3 lớp cận tối ưu =0.8: 
 ( ) =2.9 tại điểm =(3.50, 350, 700) 
 Vậy hệ số Cymax cánh 3 lớp cận tối ưu =0.8 tại điểm tối ưu tăng 101% 
so với cánh có profile đối xứng, tăng 58% so với cánh có độ cong 4% và tăng 
18% so với cánh 3 lớp phẳng tại điểm tối ưu. 
3.4. Cánh nhiều lớp thích nghi 
 Các phương án cánh 3 lớp có dây cung các cánh thành phần bằng nhau 
gặp khó khăn khi điều khiển hai cánh phía sau do tải khí động và hành trình 
chuyển vị của chúng lớn, vì vậy có thể áp dụng riêng ở một chế độ bay (ví dụ 
chế độ cất hạ cánh hoặc một chế độ bay hành trình). Để khắc phục nhược 
điểm trên, luận án đề xuất giảm khá nhiều (hơn 3 lần) kích thước dây cung 2 
cánh phía sau (hình 3.11, 3.12) với mong muốn vẫn giảm được hệ số Cx và 
tăng được hệ số Cymax so với cánh kinh điển và bằng quá trình điều khiển bộ 
tham số (α, 1, 2) đến các bộ tham số tối ưu sẽ có cánh 3 lớp thích nghi với 
các chế độ bay khác nhau. Phương án cánh 3 lớp được đề xuất có các tham số 
hình học: 
 Hình 3.11. Mặt cắt cánh 3 lớp thích nghi Hình 3.12. Hình dạng cánh 3 lớp thích nghi 
 16 
+ Dây cung cánh 3 lớp: b0=0.337[m]; Sải cánh L=1[m]; 
+ Dây cung cánh 1, cánh 2, cánh 3: b1=0.8b0, b2= b3=0.1b0; 
+ Kích thước khe hở: h1=h2=1%b0; 
+ Các cánh thành phần có profile đối xứng (profile NACA 0015). 
Khi đó độ dày lớn nhất của cánh 1:c1max=15%b1=12%b0. 
3.4.1. So sánh với cánh 1 lớp tương đương 
 Tối ưu hóa cánh 3 lớp được đề xuất ở các chế độ bay hành trình với hệ số 
Cy khác nhau và chế độ cất hạ cánh. Dưới đây là kết quả so sánh hệ số chất 
lượng khí động và hệ số Cymax so với cánh kinh điển. 
* So sánh hệ số chất lượng khí động: 
+ Khi Cy=1.6 (đại diện hệ số Cy lớn, hình 3.22): 
- K(cánh 3 lớp thích nghi)=5.4; K(cánh tối ưu Cyopt=0.3)=4.9; 
- K(cánh có độ cong 4%)=5.0; 
 Hệ số K cánh 3 lớp thích nghi tăng 8% so với cánh tối ưu Cyopt=0.3 và 
cánh có độ cong 4%, trong khi đó cánh có profile đối xứng không đạt được hệ 
số lực nâng này. 
 Hình 3.22. Đồ thị K=f(Cy) cánh 3 lớp thích nghi và các cánh 1 lớp tương đương 
+ Khi Cy=0.1 (đại diện cho hệ số Cy nhỏ, hình 3.24): 
- K(cánh 3 lớp thích nghi)=5.55; K(cánh tối ưu Cyopt=0.3)=5.48; 
- K(cánh có profile đối xứng)=5.7; K(cánh có độ cong 4%)=5.2; 
 Hệ số K cánh 3 lớp thích nghi cơ bản tương đương cánh tối ưu Cyopt=0.3, 
kém 2.6% so với cánh có profile đối xứng và cải thiện 6.7% so với cánh có độ 
cong 4%. 
+ Tương tự, ở các hệ số Cy lớn khác thì hệ số K cánh 3 lớp thích nghi vẫn duy 
trì cải thiện đáng kể so với các cánh 1 lớp. 
 17 
 Hình 3.24. Đồ thị K=f(Cy) cánh 3 lớp thích nghi và các cánh 1 lớp tương đương 
 vùng hệ số Cy nhỏ 
* So sánh hệ số lực nâng lớn nhất Cymax: 
 Kết quả tối ưu hóa hệ số lực nâng lớn nhất Cymax: 
 ( ) =2 tại điểm =(21.20, 170, 33.60) 
 Ở chế độ cất hạ cánh, ý nghĩa cánh 3 lớp thích nghi tương tự cánh sử 
dụng cánh tà có nhiều khe nhưng ở đây đã tìm được điểm tối ưu để có cánh 
thích nghi ở chế độ bay này. 
3.5. Kết luận chương 3 
 Tối ưu hóa một số phương án cánh 3 lớp và xác định được các điểm tối 
ưu tương ứng với từng chế độ bay. Phương án cánh 3 lớp có dây cung các 
cánh thành phần bằng nhau có hệ số chất lượng khí động và hệ số Cymax được 
cải thiện rất nhiều so với cánh kinh điển nhưng gặp khó khăn điều khiển 2 
cánh phía sau, vì vậy có thể áp dụng riêng ở 1 chế độ bay. Cánh 3 lớp thích 
nghi đã khắc phục được nhược điểm trên nhưng vẫn đảm bảo sự cải thiện 
đáng kể hệ số chất lượng khí động so với cánh 1 lớp. Phương án cánh này chế 
tạo khá đơn giản và điều khiển được trong khi bay nên có tính khả thi cao. 
 Chương 4. THỰC NGHIỆM KIỂM CHỨNG 
4.1. Kiểm chứng mô hình tính bằng thực nghiệm 
 Để kiểm chứng kết quả tính toán, tiến hành thí nghiệm một số mô hình 
cánh trong OTKĐ –OT để đánh giá và củng cố thêm độ tin cậy các kết quả 
tính toán. Trong điều kiện cho phép về kinh phí và thời gian nên chỉ kiểm 
chứng hiệu quả giảm hệ số Cx một số mô hình cánh tối ưu điển hình so với 
mô hình cánh có profile đối xứng. 
 18 
Mô hình thí nghiệm 
 Các mô hình cánh thí nghiệm có các tham số hình học giống với 
các kích thước cánh tương ứng ở chương 2 và chương 3, làm bằng gỗ, 
hoàn toàn đặc và được phay bằng máy CNC: 
+ Mô hình cánh có profile đối xứng (hình 4.1); 
+ Mô hình cánh tối ưu Cyopt=0.3 (hình 4.2); 
+ Mô hình cánh 3 lớp thích nghi (hình 4.3). 
 Hình 4.1. Mô hình thí nghiệm cánh có Hình 4.2. Mô hình thí nghiệm cánh tối ưu 
 profile đối xứng Cyopt=0.3 
Các phương án thí nghiệm 
+ Mô hình cánh có profile đối xứng: 
thực nghiệm tại các góc tấn: α=00, 50, 
100, 150, 200. 
+ Mô hình cánh tối ưu Cyopt=0.3: 
thực nghiệm tại các góc tấn: α=-50, 00, 
50, 100, 150, 200. 
+Mô hình cánh ba lớp thích nghi: thực Hình 4.3. Mô hình thí nghiệm cánh 3 lớp 
nghiệm tại các góc tấn và góc lệch của 2 thích nghi 
cánh phía sau: 
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(α, δ1, δ2)= (0 , 0 , 0 ), (5 , 0 , 0 ), (10 , 0 , 0 ), (0 , 10 , 18 ), (5 , 10 , 18 ); (10 , 
100, 180), (150, 100, 180), (100, 200, 280). 
4.2. Phương pháp thí nghiệm 
4.2.1. Điều kiện thí nghiệm 
 0
+ Nhiệt độ không khí:TH=14 [C]; 
+ Áp suất khí quyển ở độ cao H =0[m]: PH=760mmHg; 
 3
+ Độ ẩm không khí: 80%; Mật độ không khí: H=1.225[kg/m ]; 
+ Vận tốc dòng khí trung bình: V= 21.5[m/s]; 
+ Re 5.105; M 0.062. 
 19 
 Các mô hình cánh sử dụng trong thí nghiệm có kích thước như mô hình 
thực, các tham số của nó trong quá trình thổi thực nghiệm là các tham số đầu 
vào để tiến hành tính toán bằng lý thuyết (phần mềm Ansys) và cuối cùng là 
so sánh với kết quả thí nghiệm. Vì thế, quá trình thí nghiệm cánh mô hình 
trong OTKĐ thì các yếu tố đồng dạng hoàn toàn được đáp ứng. 
4.2.2. Phương pháp xử lý số liệu thí nghiệm 
 Các hệ số Cx, Cy, K được tính theo các công thức [7]: 
 Tương ứng mỗi thí nghiệm, máy khí động đo trong thời gian 33s, 1s đo 
được 500 kết quả. Vì vậy sẽ đo được 16500 kết quả tương ứng với các lực và 
momen khí động (Fx, Fy, Fz, Mx, My, Mz) và theo