Tóm tắt Luận án Phân tích tĩnh, ổn định và dao động riêng của tấm chữ nhật FGM sử dụng lý thuyết biến dạng cắt tám ẩn

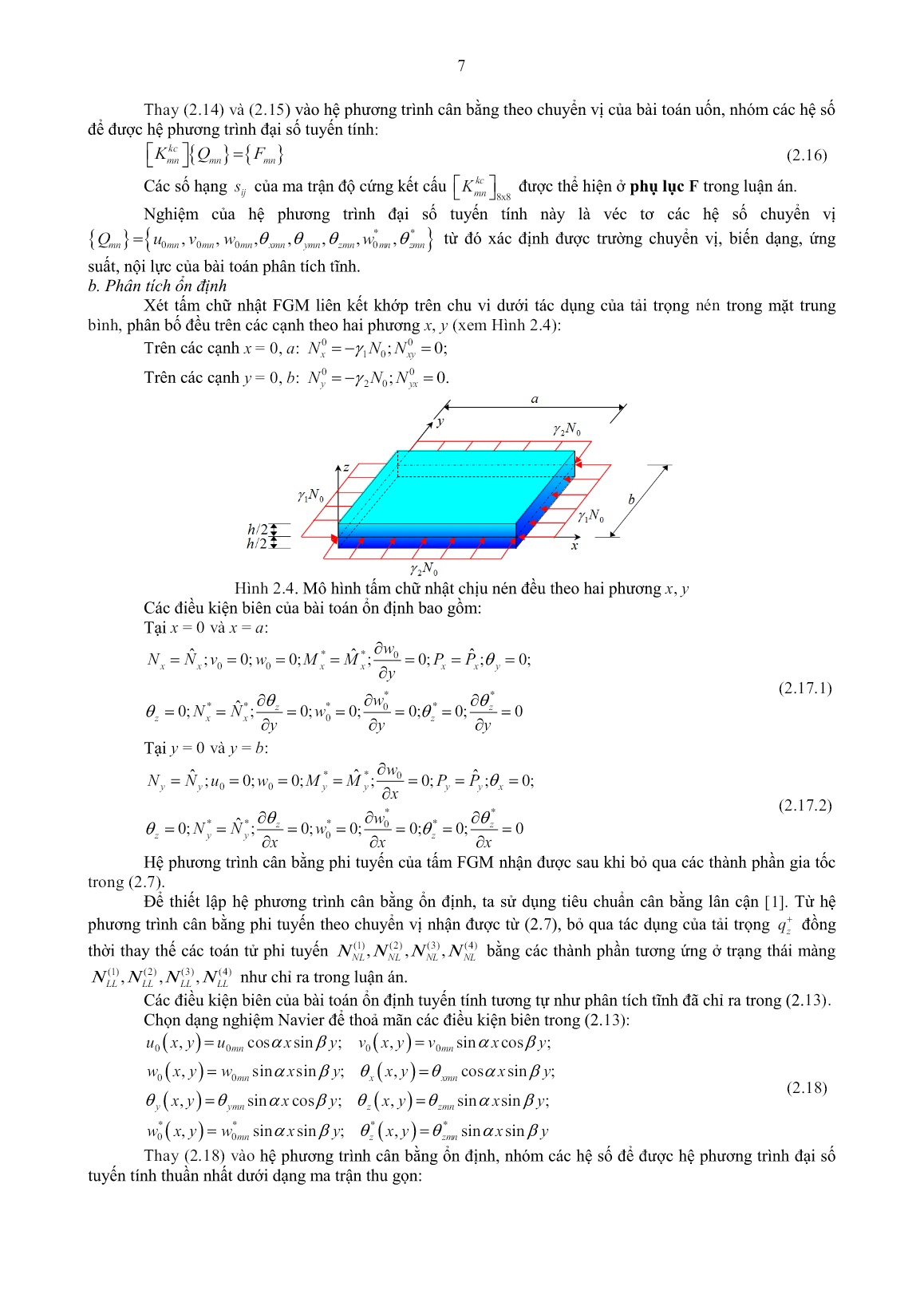
ng kết cấu 
8x8
kc
mnK được thể hiện ở phụ lục F trong luận án. 
Nghiệm của hệ phương trình đại số tu ến tính nà là véc tơ các hệ số chu ển vị 
  * *0 0 0 0, , , , , , ,mn mn mn mn xmn ymn zmn mn zmnQ u v w w    từ đó xác định được trường chu ển vị, biến dạng, ứng 
suất, nội l c của bài toán ph n tích tĩnh. 
b. Phân tích ổn định 
 ét tấm chữ nhật FGM liên kết khớp trên chu vi dưới tác dụng của tải trọng nén trong mặt trung 
bình, ph n bố đều trên các cạnh theo hai phương x, y (xem Hình 2.4): 
Trên các cạnh x = 0, a: 0 01 0; 0;x xyN N N 
Trên các cạnh y = 0, b: 0 02 0; 0.y yxN N N 
Hình 2.4. Mô hình tấm chữ nhật chịu nén đều theo hai phương x, y 
Các điều kiện biên của bài toán ổn định bao gồm: 
Tại x = 0 và x = a: 
* * 0
0 0
* *
* * * *0
0
ˆ ˆ ˆ; 0; 0; ; 0; ; 0;
ˆ0; ; 0; 0; 0; 0; 0
x x x x x x y
z z
z x x z
w
N N v w M M P P
y
w
N N w
y y y

 
 


 
  
 (2.17.1) 
Tại y = 0 và y = b: 
* * 0
0 0
* *
* * * *0
0
ˆ ˆ ˆ; 0; 0; ; 0; ; 0;
ˆ0; ; 0; 0; 0; 0; 0
y y y y y y x
z z
z y y z
w
N N u w M M P P
x
w
N N w
x x x

 
 


 
  
 (2.17.2) 
Hệ phương trình c n bằng phi tu ến của tấm FGM nhận được sau khi bỏ qua các thành phần gia tốc 
trong (2.7). 
Để thiết lập hệ phương trình c n bằng ổn định, ta sử dụng tiêu chuẩn c n bằng l n cận [1]. Từ hệ 
phương trình c n bằng phi tu ến theo chu ển vị nhận được từ (2.7), bỏ qua tác dụng của tải trọng zq
 đồng 
thời tha thế các toán tử phi tu ến (1) (2) (3) (4), , ,NL NL NL NL    bằng các thành phần tương ứng ở trạng thái màng 
(1) (2) (3) (4), , ,LL LL LL LL    như chỉ ra trong luận án. 
Các điều kiện biên của bài toán ổn định tu ến tính tương t như ph n tích tĩnh đã chỉ ra trong (2.13). 
Chọn dạng nghiệm Navier để thoả mãn các điều kiện biên trong (2.13): 
0 0 0 0
0 0
* * * *
0 0
, cos sin ; , sin cos ;
, sin sin ; , cos sin ;
, sin cos ; , sin sin ;
, sin sin ; , sin sin
mn mn
mn x xmn
y ymn z zmn
mn z zmn
u x y u x y v x y v x y
w x y w x y x y x y
x y x y x y x y
w x y w x y x y x y
  
    
     
    
 (2.18) 
Thay (2.18) vào hệ phương trình c n bằng ổn định, nhóm các hệ số để được hệ phương trình đại số 
tu ến tính thuần nhất dưới dạng ma trận thu gọn: 
8 
  0kc hhmn mn mnK N K Q 0 (2.19.1) 
trong đó: hhmnK là ma trận độ cứng hình học (các thành phần của chúng được chỉ ra trong luận án). 
L c nén mất ổn định 
mnN được xác định từ việc giải phương trình: 
 0det kc hhmn mnK N K 0 (2.19.2) 
Tải trọng tới hạn được xác định bởi: min .th mnN N 
c. Phân tích dao động riêng 
 ét tấm chữ nhật FGM liên kết khớp trên chu vi; bỏ qua toàn bộ các ếu tố tải trọng. 
Các điều kiện biên của bài toán dao động riêng t như ph n tích tĩnh đã chỉ ra trong (2.13) sau khi bổ 
sung biến thời gian t. 
Trong ph n tích dao động riêng, hệ phương trình chu ển động theo chu ển vị nhận được từ (2.7) sau 
khi bỏ qua tất cả các thành phần tải trọng và các toán tử phi tu ến (1) (2) (3) (4), , , .NL NL NL NL    
Chọn dạng nghiệm Navier để thoả mãn các điều kiện biên trong (2.13): 
0 0 0 0
0 0
* *
0 0
, , cos sin ; , , sin cos ;
, , sin sin ; , , cos sin ;
, , sin cos ; , , sin sin ;
, , sin s
mn mn
mn mn
mn mn
mn
i t i t
mn mn
i t i t
mn x xmn
i t i t
y ymn z zmn
i t
mn
u x y t u e x y v x y t v e x y
w x y t w e x y x y t e x y
x y t e x y x y t e x y
w x y t w e x
 
 
 

  
    
     
 * *in ; , , sin sinmni tz zmny x y t e x y
    
 (2.20) 
trong đó: 1;i , ;
m n
a b
  mn là tần số dao động riêng ứng với mode dao động (m, n). 
Thay (2.20) vào hệ phương trình chu ển động theo chu ển vị, nhóm các hệ số để được hệ phương 
trình đại số tu ến tính thuần nhất dưới dạng ma trận thu gọn: 
   2kcmn mn mn mnK M Q 0 (2.21.1) 
Các số hạng ijm của ma trận khối lượng  8x8mnM được thể hiện ở phụ lục F trong luận án. 
Tần số dao động riêng mn được xác định từ việc giải phương trình: 
  2det 0kcmn mn mnK M (2.21.2) 
Tần số dao động riêng cơ bản được xác định bởi: min .cb mn  
2.3.4. ơ đ khối c a chương trình tính bằng phương pháp giải tích 
Từ các biểu thức quan hệ và hệ phương trình chu ển động đã được thiết lập ở trên, chương trình tính 
viết trên nền Matlab được viết nhằm kiểm chứng các bài toán tu ến tính cho tấm chữ nhật P-FGM điều kiện 
biên khớp trên chu vi. Sơ đồ thuật toán để giải các bài toán sử dụng dạng nghiệm Navier được trình bà 
trong Luận án. 
2.4. Ví dụ kiểm chứng nghiệm giải tích 
Để kiểm chứng mô hình tấm theo lý thu ết biến dạng cắt bậc cao tám ẩn chu ển vị đề xuất (HSDT-
8), tác giả đã viết code chương trình tính d a trên lời giải Navier cho tấm chữ nhật P-FGM bốn biên t a 
khớp. Các bài toán kiển chứng được th c hiện trong luận án bao gồm: 
2.4.1. Kiểm chứng bài toán uốn 
Bài toán 1: Kiểm chứng độ võng, ứng suất pháp cho tấm đẳng hướng. 
 ét tấm vuông dà đẳng hướng (p = 0, ν = 0.3, h = 0.1m, a = b = 5h) dưới tác dụng của tải trọng 
ph n bố đều 40 10q N/m
2
. 
Bảng 2.1 trình bà một số kết quả kiểm chứng bài toán uốn cho tấm vuông đẳng hướng bao gồm độ 
võng không thứ ngu ên w và ứng suất pháp không thứ ngu ên .x 
Các kết quả của luận án được so sánh với lời giải d a trên lý thu ết đàn hồi ba chiều (3D) sử dụng 
phương pháp DSC và phương pháp HDQ của Civalek [3], lời giải 3D sử dụng phương pháp DQM của Liew 
và cộng s [7]. Các kết quả số cho thấ nghiệm giải tích (GT) d a trên lý thu ết HSDT-8 có độ tin cậ và 
cho kết quả số về độ võng không thứ ngu ên w và ứng suất pháp không thứ ngu ên x rất tốt khi so sánh 
với các kết quả tính theo lý thu ết đàn hồi 3D. 
Bảng 2.1. Kiểm chứng độ võng không thứ ngu ên và ứng suất pháp không thứ ngu ên cho tấm đẳng hướng 
9 
Nguồn 
44 0, ,0 / ;
2 2
a b
w Q w hq
0, , / .
2 2 2
x x
a b h
q
  
3D (DQM) [7] 12.6180 -7.3939 
3D (HDQ) [3] 12.6310 -7.403 
3D (DSC) [3] 12.6210 -7.403 
Luận án (GT) 12.6111 -7.3968 
Sai số (%)* -0.0547 0.0392 
*
 Sai số so với kết quả của Liew và cộng s [7]. 
Bài toán 2: Kiểm chứng ứng suất cắt ngang cho tấm đẳng hướng. Các kết quả của luận án được so 
sánh với Werner [20]. 
Bài toán 3: Kiểm chứng độ võng, ứng suất cho tấm P-FGM (Al/Al2O3-1). Các kết quả của luận án 
được so sánh với Zenkour [21], Thai và Choi [16]. 
2.4.2. Kiểm chứng bài toán ổn định 
Bài toán 1: Kiểm chứng tải trọng tới hạn cho tấm đẳng hướng. Các kết quả của luận án được so sánh 
Uymaz và Aydogdu [19], Swaminathan và Naveenkumar [12]. 
Bài toán 2: Kiểm chứng tải trọng tới hạn cho tấm P-FGM (Al/Al2O3-1). Các kết quả của luận án 
được so sánh với Thai và Choi [13]. 
2.4.3. Kiểm chứng bài toán dao động riêng 
Kiểm chứng quả tần số dao động riêng cơ bản không thứ ngu ên ˆ cho tấm P-FGM (Al/ZrO2-2). 
Các kết quả của luận án được kiểm chứng với Uymaz và Aydogdu [18]. 
2.5. Kết luận chƣơng 2 
Các kết quả chính mà chương 2 đã th c hiện bao gồm: 
1. d ng trường chu ển vị, các hệ thức và phương trình quan hệ của lý thu ết tấm biến dạng cắt 
bậc cao tám ẩn chu ển vị. Đ là một lý thu ết cải tiến thuộc nhóm lý thu ết biến dạng cắt bậc cao t a 3D 
đồng thời thỏa mãn điều kiện ứng suất cắt ngang bằng không tại mặt trên và dưới của tấm. 
2. Sử dụng ngu ên lý năng lượng toàn phần c c tiểu, các phương trình chủ đạo và điều kiện biên của 
tấm FGM theo lý thu ết biến dạng cắt bậc cao tám ẩn chu ển vị đã được thiết lập, làm cơ sở để giải các bài 
toán ph n tích tu ến tính tĩnh, ổn định và dao động riêng. 
3. Lời giải giải tích với dạng nghiệm Navier cho tấm chữ nhật FGM điều kiện biên khớp trên chu vi 
đã được x d ng (các kết quả chính được thể hiện ở các bài báo số 4 và số 9 trong danh mục các công trình 
khoa học đã công bố của tác giả). 
Các bài toán kiểm chứng cho thấ mô hình tính là tin cậ và cho kết quả tốt so với các mô hình ESL, 
đặc biệt là s chính xác hóa so với các mô hình 3D hiện có. 
Có thể thấy rằng việc xây dựng lời giải giải tích sử dụng lý thuyết biến dạng cắt bậc cao tám ẩn 
chuyển vị mới chỉ dừng lại cho dạng tấm có điều kiện biên khớp trên chu vi. Với các điều kiện biên bất kỳ 
việc đưa ra lời giải giải tích là cồng kềnh và khó khăn. Vì vậy trong chương tiếp theo, luận án sẽ xây dựng 
mô hình và thuật toán phần tử hữu hạn để phân tích ứng xử tĩnh, ổn định và dao động riêng của kết cấu tấm 
làm bằng vật liệu có cơ tính biến thiên sử dụng lý thuyết biến dạng cắt bậc cao tám ẩn chuyển vị. 
CHƢƠNG 3 
PHÂN TÍCH TĨNH, ỔN ĐỊNH VÀ DAO ĐỘNG RIÊNG CỦA TẤM CHỮ NHẬT FGM BẰNG 
PHƢƠNG PHÁP PHẦN TỬ HỮU HẠN 
3.1. Mở đầu 
Trong chương nà , vẫn d a trên lý thuyết biến dạng cắt bậc cao tám ẩn số chuyển vị, tuy nhiên luận 
án tập trung phát triển lời giải theo phương pháp phần tử hữu hạn để hoàn thiện hơn một số hạn chế như đã 
chỉ ra của phương pháp giải tích. Ngu ên lý Hamilton được sử dụng trong quá trình thiết lập phương trình 
phần tử hữu hạn; đ là cơ sở để giải quyết đồng thời ba bài toán phân tích tuyến tính bao gồm: phân tích 
tĩnh, ổn định và dao động riêng của tấm chữ nhật bằng vật liệu FGM với các dạng điều kiện biên khác nhau. 
3.2. X y dựng mô hình phần tử hữu h n 
3.2.1. Lựa chọn phần tử 
Trường chuyển vị của lý thuyết biến dạng cắt bậc cao tám ẩn số chuyển vị đòi hỏi phải sử dụng đến 
phần tử liên tục C1 khi xây d ng mô hình PTHH. Hàm nội su Lagrange ,iN   được sử dụng để biểu 
10 
diễn các chu ển vị màng 0 0,u v và góc xoay , .x y  Hàm nội su Hermite ,ijH   để biểu diễn các 
chu ển vị uốn * *0 0, , , .z zw w  
Với các ph n tích trên đ , chu ển vị tại nút thứ i của phần tử bao gồm 16 bậc t do: 
* * * * * *
0 0 0 0, 0, , , 0 0, 0, , ,, , , , , , , , , , , , , , , .i i xi yi i xi yi zi z xi z yi i xi yi zi z xi z yiu v w w w w w w        Để phù hợp với các chương trình má tính 
khi mà số bậc t do trên một nút là khá lớn mà vẫn đảm bảo độ chính xác cần thiết, luận án l a chọn sử dụng 
phần tử chữ nhật 4 nút, mỗi nút 16 bậc t do (xem Hình 3.1). 
(a) Hệ tọa độ th c (b) Hệ tọa độ t nhiên 
Hình 3.1. Phần tử chữ nhật 4 nút trong hệ tọa độ th c và hệ tọa t nhiên 
Véc tơ chu ển vị nút phần tử được biểu diễn bởi: 
  1 2 3 4, , ,
T
eq q q q q (3.1) 
trong đó:  * * * * * *0 0 0 0, 0, , , 0 0, 0, , ,, , , , , , , , , , , , , , ,
T
i i i xi yi i xi yi zi z xi z yi i xi yi zi z xi z yiq u v w w w w w w        
3.2.2. Các phương trình cơ bản 
a. Trường chuyển vị 
Véc tơ chu ển vị của một điểm bất kì trên mặt trung bình: 
  0 16 1 64 116 64 ex xx
d B q 
 (3.2) 
Như vậ , ta có thể viết lại trường chuyển vị ở dạng ma trận như sau: 
    03 1 64 1 64 13 16 16 64 3 64e ex x xx x x
d d q qH H B d 
 (3.3) 
b. Trường biến dạng 
b1. Các thành phần biến dạng tuyến tính 
     
(0) (0)
(1) (1)
0 (2) (2) 64 116 64
(3) (3)
;
mu mu
mu mu
mu e mu e xx
mu mu
mu mu
B
B
q B q
B
B





  
  
  
     
(0) (0)
(1) (1)
0 (2) (2) 64 18 64
(3) (3)
c c
c c
c e c e xx
c c
c c
B
B
q B q
B
B





  
  
  
(3.4) 
b2. Các thành phần biến dạng phi tuyến 
       1 1
1
;
2
TT TNL
x e bl bl bl bl eq B h h B q 
       2 2
1
;
2
TT TNL
y e bl bl bl bl eq B h h B q 
       2 2
TT TNL
xy e bl bl bl bl eq B h h B q 
(3.5) 
c. Trường ứng suất 
- Để khái quát hóa vấn đề, ứng suất toàn phần được định nghĩa [11]: 
   0tp   (3.6) 
11 
trong đó:  0 0 00 0 0 0
T
x y xy    là ứng suất ban đầu (do tải trọng nén trên các cạnh của 
tấm gây ra);  là ứng suất bổ sung, được xác định theo (2.10). 
3.2.3. Các liên hệ tọa độ 
Các liên hệ về tọa độ, quan hệ giữa các đạo hàm riêng trong hệ toạ độ th c và hệ toạ độ t nhiên 
được sử dụng để tính toán tích ph n số trong quá trình thành lập các ma trận độ cứng kết cấu, ma trận độ 
cứng hình học, ma trận khối lượng và véc tơ l c nút của phần tử. 
3.2.4. Phương trình phần tử hữu hạn 
Trong phương pháp phần tử hữu hạn, phương trình chu ển động của phần tử tấm FGM thu được 
bằng cách sử dụng ngu ên lý Hamilton cho hệ bảo toàn, được viết dưới dạng [10]: 
0
0
T
e e eU W T dt   
 (3.7.1) 
Hay: 
0
0
T
e e eU W T dt 
 (3.7.2) 
trong đó: eU là thế năng biến dạng đàn hồi của phần tử; eT là động năng của của phần tử; eW
là 
công ngoại l c đối với phần tử. 
Từ đ ta nhận được phương trình Lagrange loại 2 theo chu ển vị [17]: 
   
0e e e
e e e
T U Wd
dt q q q
   
    
 (3.8) 
a. Thế năng biến dạng đàn hồi của phần tử tấm được xác định bởi [11]: 
e eL eNLU U U 
 (3.9.1) 
Thế năng biến dạng đàn hồi do thành phần biến dạng tu ến tính: 
          
1 1 1
2 2 2
T T T kc
eL e eu e e ec e e e eU q k q q k q q k q 
 (3.9.2) 
Thế năng biến dạng đàn hồi do thành phần biến dạng phi tu ến: 
  0
1
2
T hh
eNL e e eU N q k q 
 (3.9.3) 
b. Công ngoại lực do tác dụng của tải trọng phân bố zq
 viết dưới dạng: 
  
T
e e eW q f 
 (3.10) 
c. Động năng của phần tử tấm được xác định bởi: 
    
1
2
T
e e e eT q m q 
 (3.11) 
d. Phương trình chuyển động: 
Thay các biểu thức (3.9-3.11) vào (3.8), phương trình chu ển động cho phần tử tấm FGM thu được 
có dạng: 
    0kc hhe e e e e em q k N k q f 
 (3.12) 
Bằng phép ghép nối các ma trận thông thường, ta nhận được phương trình phần tử hữu hạn cho toàn 
tấm: 
        0kc hhM Q K N K Q F 
 (3.13) 
trong đó  ,kcK  ,hhK  ,M Q và F tương ứng là ma trận độ cứng kết cấu, ma trận độ cứng 
hình học, ma trận khối lượng, véc tơ chu ển vị nút và véc tơ l c nút tổng thể. 
Phương trình tổng quát (3.13) có thể sử dụng để giải chuỗi bài toán uốn, ph n tích dao động riêng, 
ph n tích ổn định. Các phương trình đó có thể giải sau khi áp đặt điều kiện biên của hệ kết cấu. 
3.2.5. Tích phân số 
 Trình bà cách th c hiện tích ph n số nhằm tính toán ma trận độ cứng kết cấu, ma trận độ cứng hình 
học, ma trận khối lượng và véc tơ l c nút phần tử. 
3.2.6. Điều kiện biên 
Một số dạng điều kiện biên cho các cạnh của tấm chữ nhật FGM bao gồm: 
12 
- Biên ngàm (C): Tại x = 0; a và y = 0; b: 
0 0 0 0, 0, ,
* * * * * *
, 0 0, 0, , , 0
i i xi yi i xi yi zi z xi
z yi i xi yi zi z xi z yi
u v w w w
w w w
   
   
 (3.14) 
- Biên khớp (S): 
Tại x = 0; a: 
* * * *
0 0 0, , 0 0, , ;i yi i yi zi z yi i yi zi z yiv w w w w     
 (3.15.1) 
Tại y = 0; b: 
* * * *
0 0 0, , 0 0, ,i xi i xi zi z xi i xi zi z xiu w w w w     
 (3.15.2) 
- Biên t do (F): Tại x = 0; a và y = 0; b: 
0 0 0 0, 0, ,
* * * * * *
, 0 0, 0, , , 0
i i xi yi i xi yi zi z xi
z yi i xi yi zi z xi z yi
u v w w w
w w w
   
   
 (3.16) 
3.2.7. Sơ đ khối c a chương trình tính bằng phương pháp phần tử hữu hạn 
Từ các biểu thức quan hệ và hệ phương trình chu ển động đã được thiết lập ở trên, chương trình tính 
viết trên nền Matlab được viết nhằm kiểm chứng các bài toán tu ến tính cho tấm chữ nhật P-FGM với một số 
điều kiện biên khác nhau. Sơ đồ thuật toán để giải các bài toán sử dụng phương pháp phần tử hữu hạn được 
trình bày trong luận án. 
3.3. Ví dụ kiểm chứng thuật toán và chƣơng t ình phần tử hữu h n 
Nhằm kiểm chứng mô hình và thuật toán phần tử hữu hạn theo lý thuyết biến dạng cắt bậc cao tám 
ẩn chuyển vị, luận án đã th c hiện các bài toán sau: 
3.3.1. Kiểm chứng bài toán uốn 
Bài toán 1: Kiểm chứng độ võng, ứng suất cho tấm đẳng hướng cho hai trường hợp điều kiện biên: 
ngàm 4 cạnh (CCCC) và khớp 4 cạnh (SSSS). Các kết quả của luận án được so sánh với Civalek [3], Liew và 
cộng s [7]. 
Bài toán 2: Kiểm chứng độ võng cho tấm P-FGM (Al/ZrO2-1) cho hai trường hợp điều kiện biên: 
ngàm 4 cạnh (CCCC) và khớp 4 cạnh (SSSS). Các kết quả của luận án được so sánh với Gilhoole và cộng 
s [4], Nguyen- uan và cộng s [9], Lee và cộng s [6]; Thai và Choi [14]. 
3.3.2. Kiểm chứng bài toán ổn định 
Bài toán 1: Kiểm chứng tải trọng tới hạn cho tấm đẳng hướng điều kiện biên SSSS. Các kết quả tính 
toán của luận án được so sánh với Uymaz và Aydogdu [19]. 
Bài toán 2: Kiểm chứng tải trọng tới hạn cho tấm P-FGM (Al/SiC). Các kết quả của luận án được so 
sánh với Thai và Choi [13], Mohammadi và cộng s [8], Bodaghi và Saidi [2]. 
3.3.3. Kiểm chứng bài toán dao động riêng 
Kiểm chứng tần số dao động riêng cơ bản không thứ ngu ên ˆ cho tấm P-FGM (Al/ZrO2-2) cho ba 
trường hợp điều kiện biên: SSSS, SCSC, CCCC. Các kết quả của luận án được kiểm chứng với U maz và 
Aydogdu [18]. 
3.4. Kết luận chƣơng 3 
Các kết quả chính mà chương 3 đã th c hiện bao gồm: 
1. Xây d ng mô hình phần tử hữu hạn sử dụng lý thuyết biến dạng cắt bậc cao tám ẩn chuyển vị cho 
tấm chữ nhật FGM, trên cơ sở đó thiết lập phương trình phần tử hữu hạn để giải các bài toán tuyến tính cho 
phân tích ứng xử cơ học của tấm. 
2. Viết chương trình tính toán số trên nền Matlab: Lời giải phần tử hữu hạn cho tấm chữ nhật FGM 
với các dạng điều kiện biên đã được xây d ng (các kết quả chính được thể hiện ở bài báo số 5 trong danh 
mục các công trình khoa học đã công bố của tác giả). 
3. Đã th c hiện các ví dụ kiểm chứng cho ba bài toán phân tích tuyến tính: uốn, ổn định và dao động 
riêng của tấm chữ nhật FGM. 
Có thể thấy rằng việc xây dựng lời giải phần tử hữu hạn sử dụng lý thuyết biến dạng cắt bậc cao tám 
ẩn chuyển vị cho kết quả tốt và phù hợp với các kết quả 3D, các mô hình ESL cũng như với lời giải giải tích 
trong trường hợp điều kiện biên khớp 4 cạnh (SSSS). 
CHƢƠNG 4 
13 
KH O SÁT SỐ 
4.1. Mở đầu 
Trong chương nà , luận án sử dụng bộ chương trình t viết để khảo sát ảnh hưởng của các tham số 
vật liệu (chỉ số tỷ lệ thể tích), tham số kích thước hình học, điều kiện biên đến độ võng, các thành phần ứng 
suất, tải trọng tới hạn và tần số dao động riêng của tấm chữ nhật FGM có chiều dà không đổi sử dụng đồng 
thời 2 phương pháp: giải tích và phần tử hữu hạn. 
Trong các khảo sát tiếp theo, tấm dày chữ nhật (Hình 2.2) bằng vật liệu P-FGM với các vật liệu 
thành phần Al/Al2O3-1 được sử dụng. Mô đun đàn hồi, hệ số Poisson, khối lượng riêng của kim loại (Al): Em 
= 70 GPa, νm = 0.3, ρm = 2702 kg/m
3; của gốm (Al2O3-1): Ec = 380 GPa, νm = 0.3, ρm = 3800 kg/m
3
Ba dạng bài toán dưới đ sẽ lần lượt được th c hiện: 
 Phân tích ứng xử uốn của tấm chữ nhật bằng vật liệu FGM; 
 Phân tích ổn định tấm chữ nhật bằng vật liệu FGM chịu nén đều trên các cạnh; 
 Ph n tích dao động riêng tấm chữ nhật bằng vật liệu FGM. 
4.2. Ph n tích tĩnh 
Xét tấm chữ nhật bằng vật liệu P-FGM dưới tác dụng của tải trọng phân bố đều 40 10q N/m
2
 tác 
dụng lên bề mặt trên tấm (Hình 2.3). 
Để thuận tiện, các kết quả số về độ võng, ứng suất được thể hiện dưới dạng không thứ ngu ên dưới 
đ : 
0 0 0 0
0 0 0
1 1 1 0 0 1
0 0 0
0 0 1 1
0 0 0
1 1
( ) , , , ( ) , , , ( ) , , ,
2 2
1 1 1
( ) , , , ( ) , , , ( ) , , ;
1 1
, ,0 , , , , , , ,
2 2 2 2
c
x x y y
xy xy xz xz yz yz
c
x x xy xy
E a b
w z w z z a b z z a b z
q a q q
z a b z z a b z z a b z
q q q
E a b h h
w w a b a b
q a q q

  

  
  
  
 1 0
0
1
, ,0 .xz xz a b
q
 
 0 0 0 0 1 0 1 025 , 25 ; 1 , 1 ;
48 48 48 48
a b a b
a b a b    
(4.1) 
trong đó: 0 0 0.3399810436  là tọa độ của điểm Gauss trong hệ tọa độ t nhiên. 
4.2.1. Khảo sát biến thiên c a độ võng, ứng suất tại một điểm theo phương chiều dày 
Xét tấm chữ nhật bằng vật liệu P-FGM t a khớp trên chu vi với a = 1m, h/a = 0.2, b/a = 2. 
Biến thiên của độ võng không thứ nguyên w và các thành phần ứng suất không thứ nguyên 
, , , ,x y xy xz yz     của tấm dọc theo chiều dày tấm (z/h = -0.5 ÷ 0.5) với 5 giá trị khác nhau của chỉ số tỷ lệ 
thể tích p (p = 0, 0.5, 1, 2, 5) được tính toán và thể hiện qua các đồ thị trên Hình 4.1. 
Các đồ thị biểu diễn s biến thiên của w và , , , ,x y xy xz yz     theo chiều dà tấm với hai phương 
pháp: giải tích (GT) và phần tử hữu hạn (PTHH) rất gần nhau, điều nà khẳng định thêm độ tin cậ của mô hình 
và thuật toán. Quan sát các đồ thị nà ta thấ : 
 Độ võng w tha đổi phi tu ến theo chiều cao tấm, tu nhiên s tha đổi không nhiều; độ võng ở mặt 
dưới nhỏ hơn ở mặt trên; khi p tăng, tí