Tóm tắt Luận án Nghiên cứu mô phỏng số bôi trơn thủy động ổ đầu to thanh truyền của động đốt trong

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
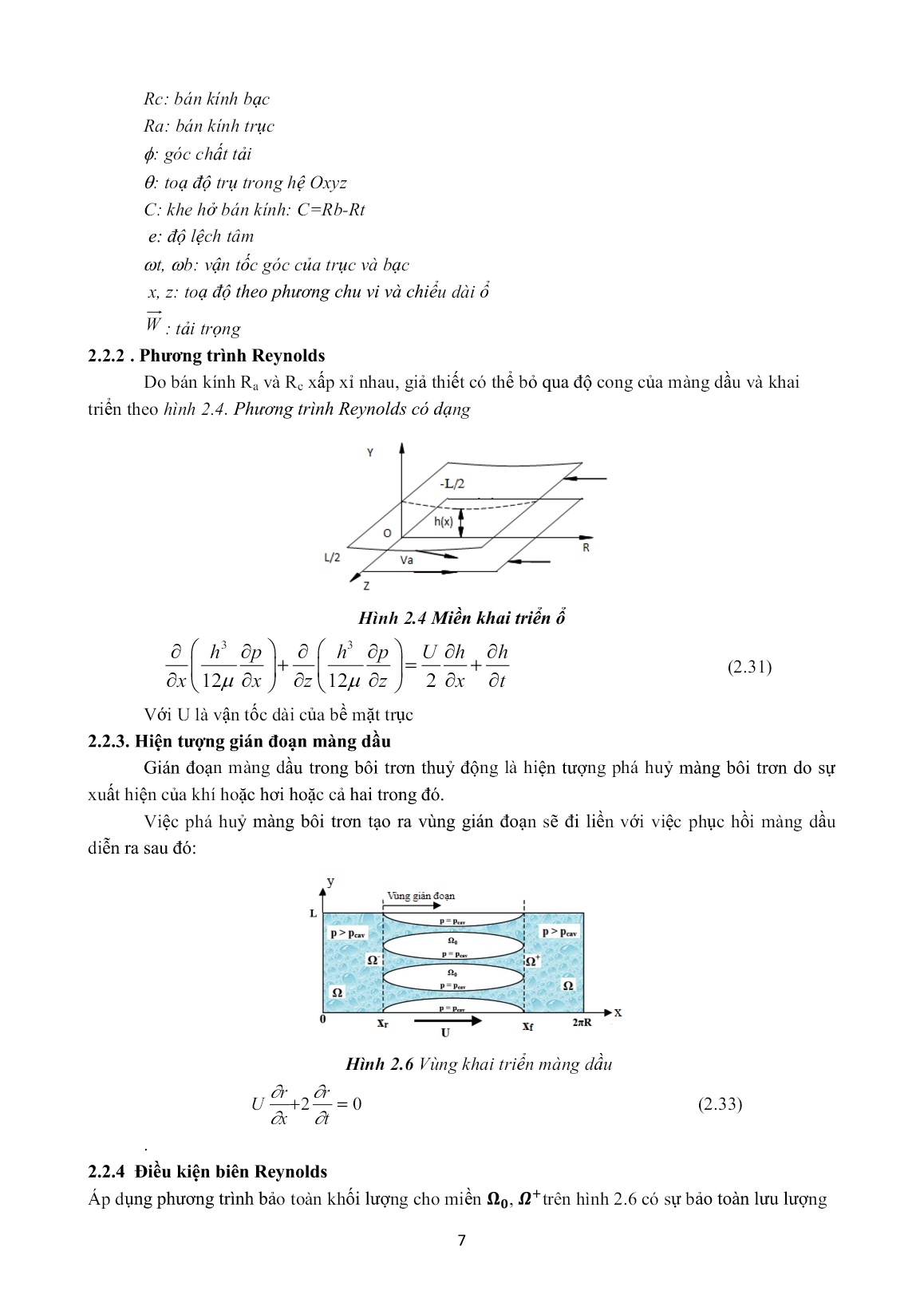
Trang 7
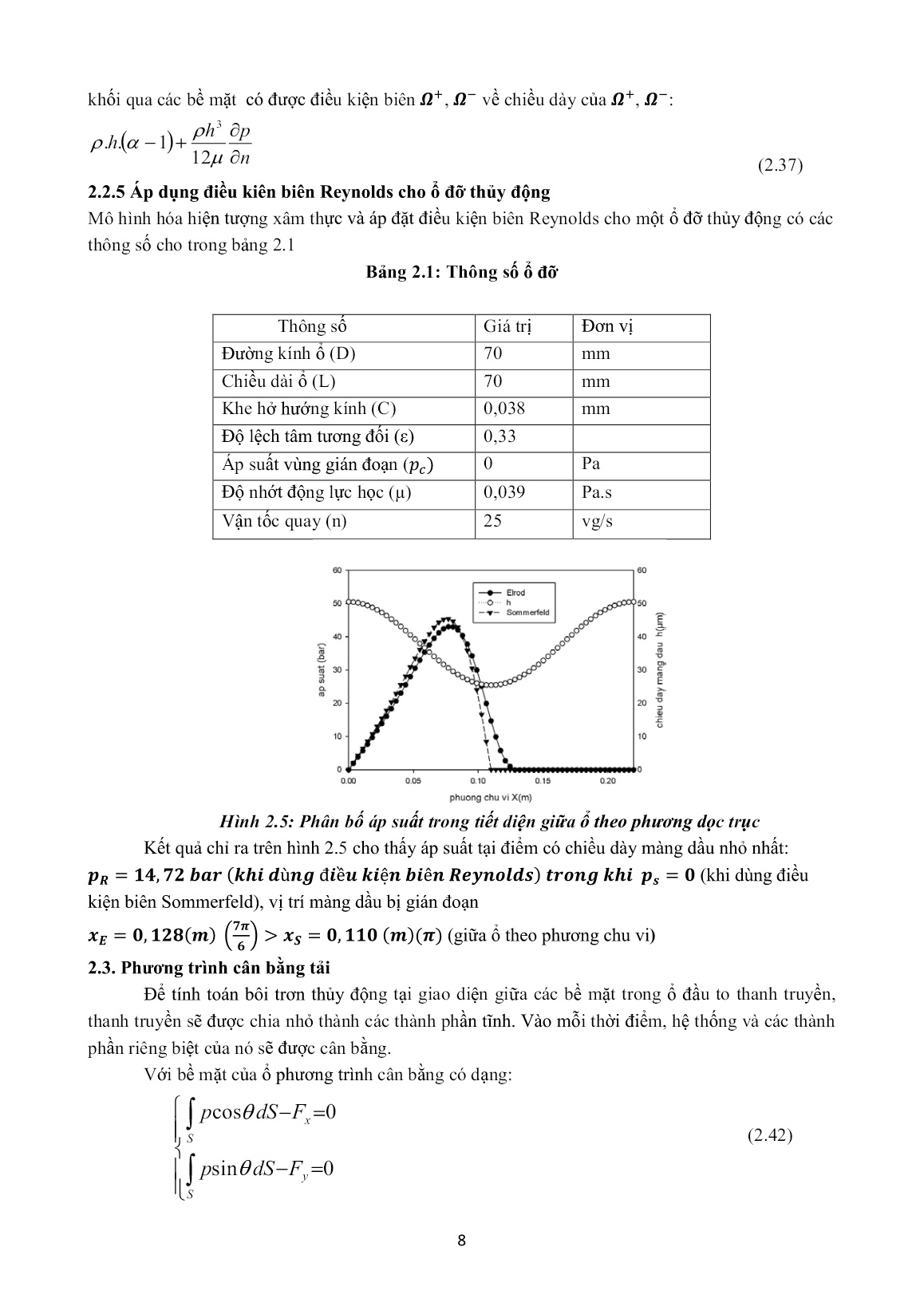
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Tóm tắt Luận án Nghiên cứu mô phỏng số bôi trơn thủy động ổ đầu to thanh truyền của động đốt trong", để tải tài liệu gốc về máy hãy click vào nút Download ở trên.
Tóm tắt nội dung tài liệu: Tóm tắt Luận án Nghiên cứu mô phỏng số bôi trơn thủy động ổ đầu to thanh truyền của động đốt trong

tâm nghiên cứu nhiều. Do vậy nước ta rất cần phát triển các nghiên cứu về bôi trơn nói chung và bôi trơn ổ đầu to thanh truyền nói riêng để làm chủ về mặt khoa học công nghệ, tiến tới hỗ trợ cho ngành công nghiệp phụ trợ, ngành công nghiệp sản xuất chế tạo phụ tùng, và tiến xa hơn là ngành công nghiệp chế tạo ô tô tại Việt Nam. Chương 2: LÝ THUYẾT BÔI TRƠN THỦY ĐỘNG 2.1. Phương trình Reynolds tổng quát Trong bôi trơn thuỷ động [10], khi coi vận tốc tại bề mặt tiếp xúc luôn tiếp xúc với chính nó và bằng cách đặt gốc của hệ trục tọa độ trên một bề mặt tiếp xúc, tức là H1 = 0 và H2 = h. Xét trong hệ toạ độ Đề các Oxyz (Hình 2.1) Các giả thiết: - Môi trường liên tục. - Chất lỏng Newton. - Dòng chảy tầng. - Bỏ qua các lực khối. - Bỏ qua các lực quán tính của dòng chảy chất lỏng. - Không có sự trượt giữa chất lỏng và các bề mặt tiếp xúc với nó. - Bỏ qua độ cong của màng mỏng chất lỏng. - Chiều dày của màng chất lỏng rất nhỏ so với kích thước của bề mặt tiếp xúc. 5 y V2 U2 y W2 2 U1 W 1 x h x 1 O O z Hình 2.1 Hệ tọa độ Điều kiện biên được viết: Trên mặt 1, với y = 0 có u = U1; v = 0; w = W1, Trên mặt 2, với y = h có u = U2; v = V2; w = W2. Trong đó: u, v, w: vận tốc của chất lỏng theo phương x, y, z. U1, V1,W1,U2, V2,W2:vận tốc của bề mặt 1 và bề mặt 2 theo phương x, y, z. ∂ ρh3 ∂p ∂ ρh3 ∂p ∂h ∂h + = 6ρ(U −U ) + 6ρ(W −W ) ∂x µ ∂x ∂z µ ∂x 1 2 ∂x 1 2 ∂z (2.1) ∂ ∂ ∂p + 6h [ρ(U +U )]+ 6h [ρ(W +W )]+12ρV +12h ∂x 1 2 ∂z 1 2 2 ∂t 2.2. Phương trình Reynolds cho ổ đỡ thuỷ động 2.2.1. Chiều dày màng dầu Hình 2.3 Hệ tọa độ xác định chiều dày màng dầu Xét trục và bạc trong hệ tọa độ xoy như hình 2.3 thì phương trình chiều dày màng dầu có dạng sau: hC(θ') =−−( 1 εxy cos θε ' sin θ ') (2.24) Trong đó εx và εy là độ lệch tâm tương đối theo hai trục x và y. Trong đó: 6 Rc: bán kính bạc Ra: bán kính trục φ: góc chất tải θ: toạ độ trụ trong hệ Oxyz C: khe hở bán kính: C=Rb-Rt e: độ lệch tâm ωt, ωb: vận tốc góc của trục và bạc x, z: toạ độ theo phương chu vi và chiểu dài ổ W : tải trọng 2.2.2 . Phương trình Reynolds Do bán kính Ra và Rc xấp xỉ nhau, giả thiết có thể bỏ qua độ cong của màng dầu và khai triển theo hình 2.4. Phương trình Reynolds có dạng Hình 2.4 Miền khai triển ổ ∂hp33 ∂ ∂ hpUhh ∂ ∂∂ +=+ (2.31) ∂x12µµ ∂ x ∂ z12 ∂ z 2 ∂∂ xt Với U là vận tốc dài của bề mặt trục 2.2.3. Hiện tượng gián đoạn màng dầu Gián đoạn màng dầu trong bôi trơn thuỷ động là hiện tượng phá huỷ màng bôi trơn do sự xuất hiện của khí hoặc hơi hoặc cả hai trong đó. Việc phá huỷ màng bôi trơn tạo ra vùng gián đoạn sẽ đi liền với việc phục hồi màng dầu diễn ra sau đó: Hình 2.6 Vùng khai triển màng dầu ∂r ∂r U +2 = 0 (2.33) ∂x ∂t . 2.2.4 Điều kiện biên Reynolds Áp dụng phương trình bảo toàn khối lượng cho miền , trên hình 2.6 có sự bảo toàn lưu lượng + 7 훀 휴 khối qua các bề mặt có được điều kiện biên , về chiều dày của , : ρh3 ∂p + − + − ρ.h.(α −1)+ 휴 휴 휴 휴 12µ ∂n (2.37) 2.2.5 Áp dụng điều kiên biên Reynolds cho ổ đỡ thủy động Mô hình hóa hiện tượng xâm thực và áp đặt điều kiện biên Reynolds cho một ổ đỡ thủy động có các thông số cho trong bảng 2.1 Bảng 2.1: Thông số ổ đỡ Thông số Giá trị Đơn vị Đường kính ổ (D) 70 mm Chiều dài ổ (L) 70 mm Khe hở hướng kính (C) 0,038 mm Độ lệch tâm tương đối (ε) 0,33 Áp suất vùng gián đoạn ( ) 0 Pa Độ nhớt động lực học (µ) 0,039 Pa.s Vận tốc quay (n) 25 vg/s Hình 2.5: Phân bố áp suất trong tiết diện giữa ổ theo phương dọc trục Kết quả chỉ ra trên hình 2.5 cho thấy áp suất tại điểm có chiều dày màng dầu nhỏ nhất: = , ( ù ê ) = (khi dùng điều kiện biên Sommerfeld), vị trí màng dầu bị gián đoạn 풑푹 ퟒ 풓 풌풉풊 풅 풏품 đ풊ề풖 풌풊ệ풏 풊 풏 푹풆풚풏풐풍풅풔 풕풓풐풏품 풌풉풊 풑풔 = , ( ) > = , ( )( ) (giữa ổ theo phương chu vi) 흅 풙2.3.푬 Phương trình � cân � bằng풙푺 tải 흅 Để tính toán bôi trơn thủy động tại giao diện giữa các bề mặt trong ổ đầu to thanh truyền, thanh truyền sẽ được chia nhỏ thành các thành phần tĩnh. Vào mỗi thời điểm, hệ thống và các thành phần riêng biệt của nó sẽ được cân bằng. Với bề mặt của ổ phương trình cân bằng có dạng: θ − = ∫ pcos dS Fx 0 S (2.42) psinθdS−F =0 ∫ y S 8 Fx và Fy là lực ngoài tác dụng dọc theo x và y, được xác định trên biểu đồ phụ tải của áp suất cháy trong một chu kỳ động cơ 2.5. Kết luận Trong chương 2 luận án đã trình bày lý thuyết tổng quan về lý thuyết bôi trơn thủy động bao gồm: -Xây dựng phương trình Reynolds tổng quát từ các phương trình cơ học của màng dầu. - Xây dựng phương trình chiều dày màng dầu và phương trình Reynolds viết cho ổ đỡ thủy động nói chung. - Mô hình hóa hiện tượng xâm thực và đưa ra điều kiện biên Reynolds cho ổ đỡ thủy động. -Áp đặt điều kiện biên Reynolds và mô phỏng hiện tượng xâm thực cho một ổ đỡ thủy động ở chế độ xác định. Kết quả chỉ ra vị trí cụ thể màng dầu bị xâm thực trong một tiết diện ổ. -Xây dựng phương trình cân bằng tải trọng với ổ đầu to thanh truyền. Các phương trình xây dựng trong chương này là cơ sở quan trọng để tác giả mô hình hóa bôi trơn cho ổ đầu to thanh truyền trong chương tiếp theo. Chương 3: MÔ PHỎNG SỐ BÔI TRƠN Ổ ĐẦU TO THANH TRUYỀN ĐỘNG CƠ 5S-FE 3.1 Mô hình hóa bôi trơn ổ đầu to thanh truyền Bài toán bôi trơn thủy động áp dụng điều kiện biên Reynolds giải quyết hai bài toán luân phiên nhau cho đến khi các kết quả hội tụ: - Bài toán 1: Biết độ lệch tâm: Xác định vị trí các vùng màng dầu liên tục và vùng gián đoạn. - Bài toán 2: Biết vị trí các vùng màng dầu liên tục và vùng gián đoạn: cân bằng tải trọng và xác định độ lệch tâm. 3.1.1 Bài toán 1 Biểu thức tích phân trọng số của phương trình vi phân [2.36] có dạng như sau: ∂hD33∂∂ ∂ hD Uhh∂∂ UDD ∂ ∂ ED()= W − F+ + + +(1 −F) +d Ω=0 ∫ ∂x12 µ∂ x ∂ y12 µ∂ y 2 ∂ xt ∂ 2 ∂ x ∂ t Ω (3.1) Với Ω là toàn bộ miền khai triển màng dầu, W là hàm trọng số khả vi trên miền Ω. Để giải quyết bài toán 1 phải chọn hàm trọng số W khác với hàm nội suy N theo phương pháp Petrov- Galerkin. Tại mỗi nút trong các phần tử của miền Ω dẫn đến một phương trình đại số tuyến tính viết dưới dạng ma trận như sau: R = [M] D + B = 0 (3.23) Ma trận [M] có cấp n, phần tử Mjk được viết: ne npg h3 nne ∂∂WW∂∂NNnne ∂ W =ω mj mk +mj mk +−mj Mjk ∑∑ m ∑ Fk ∑ NFmk (1 k ) nm=11 = 6µ k= 1∂∂xx ∂∂ zzk=1 ∂ x 1 nne −− 2 WN( 1 Ft ( )) d et J ∆ ∑ mj mk k m t k =1 (3.24) Đại lượng B trong phương trình (3.2) được tính như sau: 9 ne npg ∂h ht( ) − h ( t −∆ t) BU = ω W m +− 2mm j ∑∑ m mj nm=11 = ∂∆xt 1 nne − 2 WmjN mk(( 1()()det− FttDtt k −∆) k −∆ ) Jm ∆ ∑ t k=1 (3.25) Giải hệ phương trình trên bằng phương pháp lặp ta thu được miền liên tục và gián đoạn của màng dầu. 3.1.2. Bài toán 2 Ta có ma trận Jacobi của vecto lực: T TT S Spx Spy =−=− Jfuu () T pxy p TT (3.31) R Rp Rp xy ∂∂pp ppxy=; = ∂∂xy Viết lại phương trình 3.23 dưới dạng: Mxyp(, )= − Bxy (, ) (3.32) Đạo hàm phương trình 3.32 với các thành phần xy, ta có: =−+ + Mppxy,, MpBMpB x x y y (3.33) ∂M ∂ MBB ∂∂ Mx=, M y = ;; BB xy = = Với ∂x ∂ y ∂∂ xy Giải hệ phương trình 3.7 ta thu được vector ( ppxy, ) từ đó thay vào phương trình 3.5 ta tính được ma trận Jacobi Jfuu (). Sau đó vector u = (,xy ) được tính từ các bước nội suy theo công thức sau: (kk+ 1) () ()k u= u−− J−1 fu() fu ( ) W u (3.35) Trong đó vector W=(Fx,Fy) là vector lực tác dụng tại thời điểm t. 3.2. Thuật toán Để giải quyết liên tiếp các bài toán 1 và bài toán 2 ở các bước thời gian khác nhau tác giả xây dựng một lưu đồ thuật toán như trong các hình 3.4, hình 3.5, hình 3.6, hình 3.7. Bước xử lý dữ liệu ban đầu trong lưu đồ hình 3.4 được cụ thể trong hình 3.5 trong đó gồm quá trình đọc dữ liệu hình học của ổ đầu to thanh truyền như đường kính ổ, khe hở bán kính; dữ liệu về điều kiện làm việc như tốc độ và tải trọng ban đầu tác dụng lên ổ đầu to; dữ liệu về dầu bôi trơn như độ nhớt động học, khối lượng riêng. Sau đó là quá trình chia lưới cho ổ đầu to thanh truyền, tính toán và lưu trữ các giá trị tọa độ nút, chiều dày màng dầu tại các nút và đặt các giá trị biến trạng thái Fk ban đầu cho mỗi nút. Sau quá trình xử lý dữ liệu ban đầu chương trình đi vào vòng lặp liên tục theo bước thời gian ∆t cho đến khi hết 720o làm việc của trục khuỷu. Trong mỗi bước thời gian cần phải giải liên tiếp hai bài toán 1 và 2 cho đến khi điều kiện hôi tụ về độ lệch tâm tương đối và tải trọng thỏa mãn công thức: 10 || , , || ||+1 | | 푒 −, 푒 -6 +1 Ở đây err=10 (3.36) || ,푒 , || ≤ 푒 | |+1 | | � 퐹 ,−퐹 +1 Bài toán 1 xác định vùng liên tục퐹 và gián≤ 푒 đoạn theo lưu đồ hình 3.6, các ma trận M và B được tính theo công thức 3.24 và 3.25. Qua mỗi bước lặp ta xác định được biến trạng thái của từng nút theo giá trị D(i,j) của nút đó. Quá trình lặp kết thức khi điều kiện hội tụ của biến D thỏa mãn biểu thức: || , , || |풌|+ |풌| (3.37) 푫풙 풚 −, 푫풙 풚 풌+ Bài toán 2 xác định giá trị c푫ủ풙a풚 tải tr≤ọng풆풓풓 ứng với kết quả của bài toán 1 theo công thức 3.26 và giá trị của độ lệch tâm tương đối theo công thức 3.35 với lưu đồ trong hình 3.7. Giá trị tải trọng và độ lệch tâm này chính là giá trị ở bước lặp thứ k+1 trong các công thức 3.36 và 3.37. Để giải quyết liên tiếp các bài toán 1 và bài toán 2 ở các bước thời gian khác nhau tác giả xây dựng một lưu đồ thuật toán cho chương trình chính như trong hình 3.4 Hình 3.4 Lưu đồ thuật toán chương trình chính 3.3 Ổ đầu to thanh truyền động cơ xăng 5S-FE 3.3.1. Thanh truyền động cơ 5S-FE Thanh truyền động cơ 5S-FE (hình 3.8) bao gồm thân thanh truyền, nửa trên ổ đầu to thanh truyền lắp với nửa dưới ổ bằng hai bu-lông ghép nối. Vỏ ngoài bạc lót làm bằng thép các bon thấp, phầnhợp kim chịu mòn dùng ba bít nền thiếc cóthành phần và các tính chất cơ lý của hợp kim chịu mòn trong bảng 3.2. 11 Hình 3.8 Thanh truyền động cơ 5S-FE Độ nhám bề mặt bạc lót theo tiêu chuẩn Việt Nam TCVN 1720 – 85 về bạc lót thanh truyền yêu cầu Ra ≤ 1,25µm và độ nhám của trục khuỷu theo tiêu chuẩn Việt Nam TCVN 1705 – 85 về trục khuỷu động cơ yêu cầu Ra ≤ 0,2µm. Bảng 3.2 Thành phần và các tính chất cơ lý của hợp kim chịu mòn Độ lớn Đơn vị Tính chất cơ học -Độ cứng Brinell 24 HB -Ứng suất nén 111,5 MPa Thành phần hóa học -Thiếc (Sn) 75% -Sắt (Fe) ≤0,08% -Đồng (Cu) 3% -Arsenic (As) ≤0,15% -Antimony (Sb) 12% 3.3.2. Đo đường kính trung bình của ổ đầu to thanh truyền của động cơ 5S-FE 3.3.2.1 Mục đích - Xác định khe hở bán kính của ổ đầu to thanh truyền động cơ 5S-FE. - Xác định sự thay đổi đường kính trung bình của ổ đầu to thanh truyền của động cơ 5S-FE khi thay đổi siết bu-lông thanh truyền. 3.3.2.2 Giới thiệu thiết bị đo Máy TALYRON 365 Là máy đo khuyết tật hình dạng hình học của bề mặt các chi tiết có biên dạng trụ tròn như truc, hay ổ đỡ. Các thông số đo được trên máy bao gồm: Kích thước bán kính, đường kính, độ tròn, độ nhám, .... 3.3.2.3 Tiến trình đo 1. Đo đường kính trunng bình của bánh lệch tâm - Bánh lệch tâm được chế tạo có đường kính đúng bằng đường kính trục khuỷu của động cơ 5S-FE - Đặt chế độ, tiến hành đo đường kính của bánh lệch tâm 18 lần với bước đo 1,5mm theo chiều dài của bánh. 2. Đo đường kính trunng bình của ổ đầu to thanh truyền 12 - Ổ đầu to thanh truyền của động cơ 5S-FE, được tháo ra từ động cơ. Bạc lót ổ được mua mới để lắp thay thế. - Lần lượt tiến hành lắp hai nửa thanh truyền ở 4 siết bu-lông thanh truyền rồi đo đường kính ổ theo thứ tự 25Nm, 25Nm+300, 25Nm+600, 25Nm+900 26.0330 26.0320 26.0310 26.0300 26.0290 26.0280 26.0270 0 5 10 15 20 Hình 3.13 Kết quả đo đường kính ổ đầu to thanh truyền 25Nm+300 3.3.3 Kết quả thực nghiệm Trong hình 3.3 trình bày kết quả đo bán kính ổ đầu to thanh truyền 5S-FE tại siết bu-lông thanh truyền 25Nm+300. Quá trình đo được thực hiện ở 18 tiết diện theo chiều trục, bán kính thay đổi từ giá trị nhỏ nhất là 26,0277 (mm) đến giá trị lớn nhất 26,032 (mm). Bảng 3.3 Đường kính ổ đầu to thanh truyền theo siết bu-lông thanh truyền TT Lực siết bu lông Bán kính trung Bán kính bánh lệch Khe hở bán kính bình ổ (mm) tâm (mm) (mm) 1 25Nm 26,029 26,005 0,024 2 25Nm+300 26,043 26,005 0,038 3 25Nm+600 26,060 26,005 0,055 4 25Nm+900 26,073 26,005 0,069 3.3.4. Tải tác dụng lên ổ đầu to thanh truyền động cơ 5S-FE Tải trọng tác dụng lên thanh truyền trong thiết bị thực nghiệm sẽ mô phỏng lại quá trình làm việc của động cơ qua bốn kỳ: hút, nén, nổ, xả. Tải trọng gồm hai lực, lực kéo nén Fx và lực uốn Fy. Các lực này được hệ thống đo của băng thử MEGAPASCALE (Hình 3.15) lưu trữ vào một file dữ liệu từ đó tác giả xây dựng được biểu đồ tải theo các góc của trục khuỷu trong một chu kỳ làm việc như hình 3.16. Hình 3.15 Trung tâm điều khiển băng thử khi thực nghiệm MEGAPASCALE 13 Hình 3.16 Tải tác dụng lên ổ đầu to thanh truyền 3.4 Kết quả mô phỏng số Với giải thuật đã trình bày trong mục 3.2, ổ đầu to thanh truyền được chia thành các phần tử chữ nhật 4 nút trong đó phương chu vi được chia thành 60 phần và phương dọc trục được chia thành 20 phần. Tác giả đã viết chương trình tính toán đặc tính bôi trơn ổ đầu to thanh truyền bằng ngôn ngữ lập trình Fortran 95 (Phụ lục 3.2). Kết quả thu được gồm áp suất màng dầu, chiều dày màng dầu và độ lệch tâm tương đối. Kết quả thu được gồm áp suất màng dầu, chiều dày màng dầu và độ lệch tâm tương đối. a, Chia lưới ổ đầu to thanh truyền b, Hệ tọa độ thanh truyền Hình 3.17 Chia lưới ổ đầu to thanh truyền 3.4.1. Áp suât màng dầu Hình 3.18 biểu diễn phân bố áp suất của ổ đầu to thanh truyền theo phương chu vi tại ba tiết diện L/2, L/5, L/10 của chiều dài ổ khi khe hở bán kínhC = 24µm ở vị trí 3700 của trục khuỷu thuộc kì nổ. Phân bố áp suất bắt đầu ở vị trí 1080 và kết thúc ở 2970 theo phương chu vi. Ta thấy, phần chân của phân bố áp suất biến thiên nhỏ tuy nhiên đỉnh của phân bố rất cao tại 2790 của trục khuỷu áp suất lớn nhất là 57.7 MPa, đến 2340 của trục khuỷu áp suất lớn nhất là 7.4 MPa. Hình 3.18 Phân bố áp suất theo phương chu vi tại 3700 của trục khuỷu khi khe hở bán kính C = 24µm 14 Hình 3.19 Phân bố áp suất theo phương chiều dài tại 3700 của trục khuỷu khi khe hở bán kính C = 24µm Hình 3.19 biểu diễn phân bố áp suất theo phương chiều dài ổ tại ba tiết diện theo chiều dài ổ tại 2790, 2520 và 2160 của phương chu vi khi khe hở bán kính C = 24µm ở vị trí 3700 của trục khuỷu. Theo hình, áp suất phân bố đối xứng theo phương chiều dài qua vị trí giữa ổ. Tại một tiết diện, tốc độ biến thiên của áp suất nhỏ tuy nhiên sự chênh lệch giữa các tiết diện khác nhau rất lớn. Hình 3.20 biểu diễn phân bố áp suất của ổ đầu to thanh truyền với C = 24µm ở vị trí 3700 của trục khuỷu. Theo đó, phần chịu lực chính tập trung tại một vùng diện tích nhỏ về phía nửa cuối của ổ theo chiều quay. Hình 3.20 Phân bố áp suất tại góc 3700 của trục khuỷu khi khe hở bán kính C = 24µm Hình 3.21 biểu diễn phân bố áp suất tại tiết diện giữa ổ theo phương chu vi tại các góc 200, 1700, 3200, 3500, 470o của trục khuỷu với khe hở bán kính C = 24µm. Theo biểu đồ, phân bố áp suất dịch chuyển theo góc quay của trục khuỷu cùng với các kỳ làm việc hút – nén - nổ - xả. Ta thấy, càng gần với kỳ nổ đỉnh phân bố áp suất càng nhọn, cao hơn so với các vùng khác. Phân bố đạt cực đại giảm về hai phía kể từ vị trí xảy ra sự nổ (khoảng 370o) với áp suất lớn nhất lần lượt là o o o pmax,370 (nổ) = 57.7 MPa, pmax,350 (nén) = 26.6 MPa, pmax,20 (hút) = 11.4 MPa. Trải qua một chu kỳ làm việc phân bố áp suất chủ yếu tập trung phần phía sau của ổ theo chiều quay. 15 Hình 3.21 Phân bố áp suất tại tiết diện giữa ổ theo phương chu vi tại các góc 200, 3200, 3500, 3700 của trục khuỷu khi khe hở bán kính C = 24µm Hình 3.23 và hình 3.24 biểu diễn phân bố áp suất tại góc 200 và 7000 của trục khuỷu là điểm thuộc nửa đầu kỳ hút và nửa cuối kỳ xả với khe hở bán kính C = 24µm. Tại điểm thuộc kỳ hút lực tác dụng FX = - 2962 (N), FY = - 607 (N). Tại điểm thuộc kỳ xả lực tác dụng FX= - 3000 (N), o FY = 680 (N). Phân bố áp suất ở cả hai điểm này chia ra hai nửa của ổ nhưng phía sau rất thấp (p20 o o = 64KPa, p700 = 0.2 MPa), phần chịu tải chính tập trung nửa đầu của ổ với pmax,20 = 11.4 MPa, o pmax,700 = 12.1 MPa. Hình 3.23 Phân bố áp suất tại góc 200 của trục khuỷu khi khe hở bán kính C = 24µm Hình 3.24 Phân bố áp suất tại góc 7000 của trục khuỷu khi khe hở bán kính C = 24µm Hình 3.25 Phân bố áp suất tại góc 3200 của trục khuỷu khi khe hở bán kính C = 24µm 16 Hình 3.25 biểu diễn phân bố áp suất tại góc 3200 của trục khuỷu là điểm thấp nhất thuộc kỳ nén với C = 24µm. Tại điểm này lực tác dụng FX = 0 (N), FY = 1934 (N).Phân bố áp suất trải ra hai đầu ổ tuy nhiên đỉnh của phân bố thấp nhất pmax = 7.3 MPa. Hình 3.14 biểu diễn sự thay đổi phân bố áp suất theo khe hở bán kínhtại tiết diện giữa ổ theo phương chu vi tại góc 370o của trục khuỷu.Khe hở bán kính lần lượt là C = 24µm, C = 38µm, C = 55µm, C = 69µm. Ta thấy, khi tăng khe hở hướng kính, đỉnh của phân bố áp suất tăng, áp suất lớn nhất theo khe hở hương kính lần lượt là:pmax,C=24µm = 57.7 MPa, pmax,C=38µm = 60.5 MPa, pmax,C=55µm = 63.6 MPa, pmax,C=69µm = 68.7 MPa. Hình 3.26 Phân bố áp suất tại tiết diện giữa ổ theo phương chu vi tại góc 3700 của trục khuỷu với C = 24µm, C = 38µm, C = 55µm, C = 69µm Hình 3.26 biểu diễn thay đổi của áp suất màng dầu lớn nhất pmax theo các góc quay của trục khuỷu tại bốn khe hở bán kính C = 24µm, C = 38µm, C = 55µm, C = 69µm. Theo đồ thị, khi độ 0 lệch tâm tăng, áp suất lớn nhất pmax tăng, giá trị tăng lớn nhất tại góc 370 của trục khuỷu. Hình 3.27 Áp suất màng dầu lớn nhất khi C = 24µm, C = 38µm, C = 55µm, C = 69µm 3.4.2. Chiều dày màng dầu Hình 3.28 biểu diễn sự thay đổi của chiều dày màng dầu nhỏ nhất hmin và áp suất màng dầu lớn nhất pmax theo góc quay của trục khuỷu qua bốn kỳ hút-nén-nổ-xả khi khe hở bán kính C = 24µm. Theo đó áp suất màng dầu lớn nhất và chiều dày màng dầu nhỏ nhất tại vị trí xảy ra sự nổ: pmax = 57.7 MPa, hmin = 3,334 µm. Tại vùng áp suất pmax tăng thì chiều dày màng dầu nhỏ nhất hmin 0 giảm. Chiều dày màng dầu nhỏ nhất đạt giá trị lớn nhất hmin,max = 8,0431 µm tại góc 80 của trục khuỷu. 17 Hình 3.28 Chiều dầy màng dầu nhỏ nhất hmin, áp suất màng dầu lớn nhất pmax theo góc quay của trục khuỷu với C = 24µm 3.4.3. Độ lệch tâm trục – bạc Hình 3.29 biểu diễn quỹ đạo của tâm trục khuỷu quanh tâm thanh truyền theo một chu kỳ tải. Quỹ đạo của tâm trục quanh tâm ổ đầu to thanh truyền theo một chu kỳ tải là một đường cong 0 o o khép kín bắt đầu từ 0 của trục khuỷu, độ lệch tâm tương đối εx,0 = - 0.6656, εy,0 = - 0.3895 thuộc góc phần tư thứ I. Sau đó tâm trục dịch chuyển theo thứ tự các góc phần tư I-II-III-II-III-IV khi tải tác dụng thay đổi. Hình 3.29 Độ lệch tâm tương đối của thanh truyền và trục khi khe hở bán kính C = 24µm Hình 3.30 Độ lệch tâm tương đối của thanh truyền và trục khi thay đổi khe hở bán kính 18 Hình 3.30 biểu diễn quỹ đạo của tâm trục quanh tâm thanh truyền tại các khe hở bán kính khác nhau. Khi tăng khe hở bán kính thì quỹ đạo tâm trục có dạng tương đồng nhau, tuy nhiên nó o o có xu hướng dịch chuyển về phía có ɛx≈1: εx,370 = 0.8200, εy,370 = 0.3304. 3.5.Kết luận Trong chương 3 luận án đã nghiên cứu các vấn đề để tiến hành xây dựng thành công một chương trình tính toán số các đặc tính bôi trơn thủy động ổ đầu to thanh truyền. Bao gồm các vấn đề sau đây. - Xây dựng mô hình tính toán bôi trơn thủy động cho ổ đầu to thanh truyền cũng như thuật toán để giải bài toán. - Lập t
File đính kèm:
 tom_tat_luan_an_nghien_cuu_mo_phong_so_boi_tron_thuy_dong_o.pdf
tom_tat_luan_an_nghien_cuu_mo_phong_so_boi_tron_thuy_dong_o.pdf PHỤ LỤC LUẬN ÁN.pdf
PHỤ LỤC LUẬN ÁN.pdf Thông tin LUẬN ÁN (Tiếng Anh).pdf
Thông tin LUẬN ÁN (Tiếng Anh).pdf Thông tin LUẬN ÁN (Tiếng việt).pdf
Thông tin LUẬN ÁN (Tiếng việt).pdf TRÍCH YẾU LUẬN ÁN.pdf
TRÍCH YẾU LUẬN ÁN.pdf

